- Find the derivative of a function
- Draw the derivative’s graph using the original function’s graph
- Explain what it means for a function to be differentiable and how this is connected to being continuous
- Calculate derivatives beyond the first order
Derivative Functions
As we have seen, the derivative of a function at a given point gives us the rate of change or slope of the tangent line to the function at that point. If we differentiate a position function at a given time, we obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every point would produce valuable information about the behavior of the function. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would quickly become quite tedious.
The derivative function gives the derivative of a function at each point in the domain of the original function for which the derivative is defined. We can formally define a derivative function as follows.
derivative function
Let [latex]f[/latex] be a function. The derivative function, denoted by [latex]f^{\prime}[/latex], is the function whose domain consists of those values of [latex]x[/latex] such that the following limit exists:
A function [latex]f(x)[/latex] is said to be differentiable at [latex]a[/latex] if [latex]f^{\prime}(a)[/latex] exists. More generally, a function is said to be differentiable on [latex]S[/latex] if it is differentiable at every point in an open set [latex]S[/latex], and a differentiable function is one in which [latex]f^{\prime}(x)[/latex] exists on its domain.
In the next few examples we use the definition to find the derivative of a function. There are a few algebraic techniques that are commonly used when using this definition. It may be useful to recall these techniques.
- Greatest Common Factor (GCF): The GCF of a polynomial is the largest polynomial that divides evenly into each term of the polynomial. When using the difference quotient, you will often need to factor out a GCF of [latex]h[/latex]
- Conjugate: For a numerator or a denominator containing the sum or difference of a rational and an irrational term, multiply the numerator and denominator by the conjugate, which is found by changing the sign of the radical portion of the denominator. If the denominator is [latex]a+b\sqrt{c}[/latex], then the conjugate is [latex]a-b\sqrt{c}[/latex].
Find the derivative of [latex]f(x)=\sqrt{x}[/latex].
Find the derivative of the function [latex]f(x)=x^2-2x[/latex].
We use a variety of different notations to express the derivative of a function. In the previous example, we showed that if [latex]f(x)=x^2-2x[/latex], then [latex]f^{\prime}(x)=2x-2[/latex].
If we had expressed this function in the form [latex]y=x^2-2x[/latex], we could have expressed the derivative as [latex]y^{\prime}=2x-2[/latex] or [latex]\frac{dy}{dx}=2x-2[/latex]. We could have conveyed the same information by writing [latex]\frac{d}{dx}(x^2-2x)=2x-2[/latex].
Thus, for the function [latex]y=f(x)[/latex], each of the following notations represents the derivative of [latex]f(x)[/latex]:
In place of [latex]f^{\prime}(a)[/latex] we may also use [latex]\frac{dy}{dx}\Big|_{x=a}[/latex]. Using the [latex]\frac{dy}{dx}[/latex] notation (called Leibniz notation) is quite common in engineering and physics.
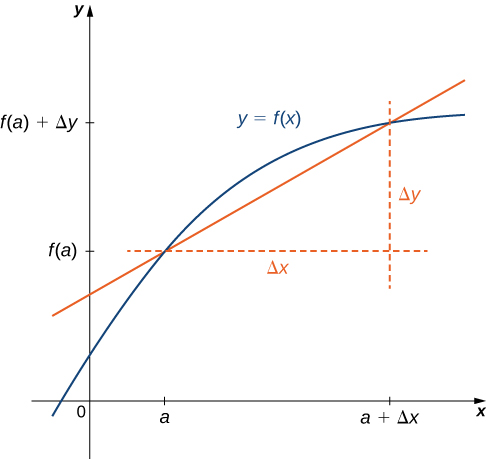
To understand this notation better, recall that the derivative of a function at a point is the limit of the slopes of secant lines as the secant lines approach the tangent line.
The slopes of these secant lines are often expressed in the form [latex]\frac{\Delta y}{\Delta x}[/latex] where [latex]\Delta y[/latex] is the difference in the [latex]y[/latex] values corresponding to the difference in the [latex]x[/latex] values, which are expressed as [latex]\Delta x[/latex] (Figure 1).
Thus the derivative, which can be thought of as the instantaneous rate of change of [latex]y[/latex] with respect to [latex]x[/latex], is expressed as