The Derivative as a Function: Fresh Take

  • Find the derivative of a function
  • Draw the derivative’s graph using the original function’s graph
  • Explain what it means for a function to be differentiable and how this is connected to being continuous
  • Calculate derivatives beyond the first order

Derivative Functions

The Main Idea 

  • Derivative Function:
    • Gives the derivative of a function at every point in its domain
    • Defined as: [latex]f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}[/latex]
  • Differentiability:
    • A function is differentiable at a point if its derivative exists at that point
    • A function is differentiable on an interval if it’s differentiable at every point in that interval
  • Notation for Derivatives:
    • [latex]f'(x)[/latex], [latex]y'[/latex], [latex]\frac{dy}{dx}[/latex], [latex]\frac{d}{dx}(f(x))[/latex]
  • Leibniz Notation:
    • [latex]\frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}[/latex]
    • Represents instantaneous rate of change

Find the derivative of [latex]f(x)=x^2[/latex].

Watch the following video to see the worked solution to this example.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “3.2 The Derivative as a Function” here (opens in new window).

Find the derivative of [latex]f(x) = x^3 + 2x[/latex].

Graphing a Derivative

The Main Idea 

  • Graphical Relationship:
    • The derivative [latex]f'(x)[/latex] represents the slope of the tangent line to [latex]f(x)[/latex]
    • Positive [latex]f'(x)[/latex] indicates [latex]f(x)[/latex] is increasing
    • Negative [latex]f'(x)[/latex] indicates [latex]f(x)[/latex] is decreasing
    • Zero [latex]f'(x)[/latex] indicates [latex]f(x)[/latex] has a horizontal tangent
  • Key Features:
    • Local maxima/minima of [latex]f(x)[/latex] correspond to zeros of [latex]f'(x)[/latex]
    • Inflection points of [latex]f(x)[/latex] correspond to local extrema of [latex]f'(x)[/latex]
    • Vertical asymptotes of [latex]f(x)[/latex] may correspond to infinite limits of [latex]f'(x)[/latex]

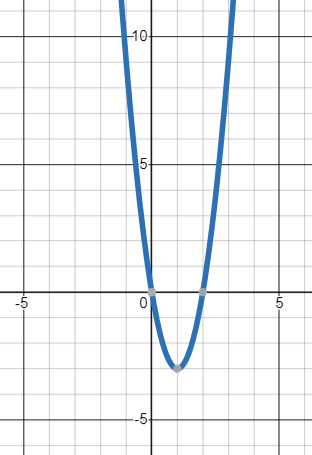
Sketch the graph of [latex]f(x)=x^2-4[/latex]. On what interval is the graph of [latex]f^{\prime}(x)[/latex] above the [latex]x[/latex]-axis?

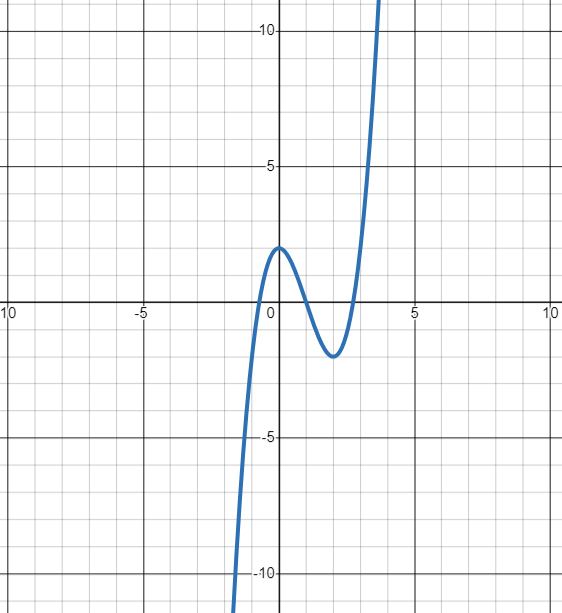
Given the graph of [latex]f(x) = x^3 - 3x^2 + 2[/latex], sketch the graph of [latex]f'(x)[/latex].

A graph of the function f(x) = x³ - 3x² + 2 on a coordinate plane. The blue curve starts in the lower left quadrant, rises steeply, reaches a local maximum around x=0, dips to a local minimum, then rises steeply again in the upper right quadrant. The graph shows two turning points, creating an S-shaped curve characteristic of a cubic function.
Graph of the cubic function f(x) = x³ – 3x² + 2.

Derivatives and Continuity

The Main Idea 

  • Differentiability implies Continuity:
    • If a function is differentiable at a point, it must be continuous there
    • The converse is not true: continuity does not imply differentiability
  • Reasons for Non-differentiability:
    • Sharp corners (e.g., absolute value function at [latex]x = 0[/latex])
    • Vertical tangents (e.g., cube root function at [latex]x = 0[/latex])
    • Oscillating behavior (e.g., [latex]x \sin(\frac{1}{x})[/latex] near [latex]x = 0[/latex])
  • Conditions for Differentiability:
    • Function must be continuous at the point
    • Left-hand and right-hand derivatives must exist and be equal

Find values of [latex]a[/latex] and [latex]b[/latex] that make the following function both continuous and differentiable at [latex]x = 2[/latex]:

[latex]f(x) = \begin{cases} ax^2 + bx & \text{if } x < 2 \\ x + 4 & \text{if } x \geq 2 \end{cases}[/latex]

Analyze the continuity and differentiability of the following function:

[latex]f(x) = \begin{cases} x^2 & \text{if } x \leq 0 \\ \sqrt{x} & \text{if } x > 0 \end{cases}[/latex]

Find all points where the following function is not differentiable:

[latex]f(x) = |x^2 - 4x + 3|[/latex]

Higher-Order Derivatives

The Main Idea 

  • Definition:
    • Higher-order derivatives are the result of repeatedly differentiating a function
    • Second derivative: derivative of the first derivative
    • Third derivative: derivative of the second derivative, and so on
  • Notation:
    • For [latex]y = f(x)[/latex]:
      • Second derivative: [latex]f''(x)[/latex], [latex]y''[/latex], or [latex]\frac{d^2y}{dx^2}[/latex]
      • Third derivative: [latex]f'''(x)[/latex], [latex]y'''[/latex], or [latex]\frac{d^3y}{dx^3}[/latex]
      • [latex]n[/latex]th derivative: [latex]f^{(n)}(x)[/latex], [latex]y^{(n)}[/latex], or [latex]\frac{d^ny}{dx^n}[/latex]
  • Physical Interpretations:
    • First derivative of position: velocity
    • Second derivative of position: acceleration
    • Higher derivatives: rates of change of acceleration, etc.

Find [latex]f''(x)[/latex] for [latex]f(x)=x^2[/latex].

Watch the following video to see the worked solution to this example.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end. You can view the transcript for this segmented clip of “3.2 The Derivative as a Function” here (opens in new window).

Find the first four derivatives of [latex]f(x) = x^4 - 2x^3 + 3x^2 - 4x + 5[/latex].

For [latex]s(t)=t^3[/latex], find [latex]a(t)[/latex].