- Recognize the parts of an integral and when it can be used
- Explain how definite integrals relate to the net area under a curve and use geometry to evaluate them
- Determine the average value of a function
Defining and Evaluating Definite Integrals
The Main Idea
- Definition of Definite Integral:
- Generalizes the concept of area under a curve
- [latex]\int_a^b f(x) dx = \lim_{n \to \infty} \sum_{i=1}^n f(x_i^*)\Delta x[/latex]
- Function [latex]f(x)[/latex] is integrable if this limit exists
- Components of Definite Integral Notation:
- [latex]\int[/latex]: Integration symbol (elongated [latex]S[/latex])
- [latex]a, b[/latex]: Limits of integration (lower and upper)
- [latex]f(x)[/latex]: Integrand
- [latex]dx[/latex]: Variable of integration
- Integrability:
- Continuous functions on [latex][a,b][/latex] are integrable
- Some discontinuous functions may also be integrable
- Evaluation Methods:
- Using the definition (Riemann sums)
- Geometric formulas for area
- More advanced techniques (to be learned later)
Use the definition of the definite integral to evaluate [latex]\displaystyle\int_0^3 (2x-1) dx[/latex]. Use a right-endpoint approximation to generate the Riemann sum.
Area and the Definite Integral
The Main Idea
- Net Signed Area:
- Represents the area between the curve and the [latex]x[/latex]-axis, taking into account the sign of the function
- [latex]\int_a^b f(x) dx = A_1 - A_2[/latex]
- [latex]A_1[/latex]: Area above [latex]x[/latex]-axis, [latex]A_2[/latex]: Area below [latex]x[/latex]-axis
- Can be positive, negative, or zero
- Total Area:
- Represents the total area between the curve and the [latex]x[/latex]-axis, regardless of the function’s sign
- [latex]\int_a^b |f(x)| dx = A_1 + A_2[/latex]
- Always non-negative
- Interpretation of Definite Integrals:
- For positive functions: Area under the curve
- For functions that change sign: Net signed area
- Using absolute value: Total area
- Application to Displacement:
- Velocity function [latex]v(t)[/latex]: Area under curve represents displacement
- Net signed area: Final position relative to starting point
- Total area: Total distance traveled
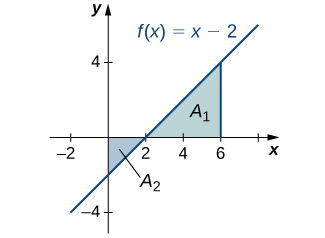
Find the net signed area of [latex]f(x)=x-2[/latex] over the interval [latex][0,6][/latex], illustrated in the following image.
Find the total area between the function [latex]f(x)=2x[/latex] and the [latex]x[/latex]-axis over the interval [latex][-3,3][/latex].
Properties of the Definite Integral
The Main Idea
- Basic Properties of Definite Integrals:
- Zero interval:
- [latex]\int_a^a f(x) dx = 0[/latex]
- Reversing limits:
- [latex]\int_b^a f(x) dx = -\int_a^b f(x) dx[/latex]
- Sum rule:
- [latex]\int_a^b [f(x)+g(x)] dx = \int_a^b f(x) dx + \int_a^b g(x) dx[/latex]
- Difference rule:
- [latex]\int_a^b [f(x)-g(x)] dx = \int_a^b f(x) dx - \int_a^b g(x) dx[/latex]
- Constant multiple:
- [latex]\int_a^b cf(x) dx = c \int_a^b f(x) dx[/latex]
- Splitting interval:
- [latex]\int_a^b f(x) dx = \int_a^c f(x) dx + \int_c^b f(x) dx[/latex]
- Zero interval:
- Comparison Theorem (for [latex]a \le b[/latex]):
- Non-negative function:
- If [latex]f(x) \ge 0[/latex] for [latex]a \le x \le b[/latex], then [latex]\int_a^b f(x) dx \ge 0[/latex]
- Comparing functions:
- If [latex]f(x) \ge g(x)[/latex] for [latex]a \le x \le b[/latex], then [latex]\int_a^b f(x) dx \ge \int_a^b g(x) dx[/latex]
- Bounded function:
- If [latex]m \le f(x) \le M[/latex] for [latex]a \le x \le b[/latex], then [latex]m(b-a) \le \int_a^b f(x) dx \le M(b-a)[/latex]
- Non-negative function:
Use the properties of the definite integral to express the definite integral of [latex]f(x)=6x^3-4x^2+2x-3[/latex] over the interval [latex][1,3][/latex] as the sum of four definite integrals.
If it is known that [latex]\displaystyle\int_1^5 f(x) dx = -3[/latex] and [latex]\displaystyle\int_2^5 f(x) dx = 4[/latex], find the value of [latex]\displaystyle\int_1^2 f(x) dx[/latex].
Average Value of a Function
The Main Idea
- Definition of Average Value:
- For a function [latex]f(x)[/latex] continuous on [latex][a,b][/latex], the average value is: [latex]f_{\text{ave}} = \frac{1}{b-a} \int_a^b f(x) dx[/latex]
- Interpretation:
- Generalizes the concept of arithmetic mean to continuous functions
- Represents the height of a rectangle with base [latex][a,b][/latex] and equal area to that under the curve of [latex]f(x)[/latex]
- Derivation:
- Based on Riemann sums:
- [latex]\frac{1}{b-a}\lim_{n\to \infty}\sum_{i=1}^{n} f(x_i^*) \Delta x[/latex]
- Limit of Riemann sum becomes the definite integral
- Based on Riemann sums:
- Applications:
- Physics: Average velocity, average power, etc.
- Economics: Average cost, average revenue, etc.
- Statistics: Expected value of a continuous random variable
Find the average value of [latex]f(x)=6-2x[/latex] over the interval [latex][0,3][/latex].
Find the average value of [latex]f(x) = x^2[/latex] on the interval [latex][0,2][/latex].