Derivatives of Trigonometric Functions

For the following exercises (1-5), find $\frac{dy}{dx}$ for the given functions.

1. $y=x^2- \sec x+1$
2. $y=x^2 \cot x$
3. $y=\dfrac{\sec x}{x}$
4. $y=(x+ \cos x)(1- \sin x)$
5. $y=\dfrac{1- \cot x}{1+ \cot x}$

For the following exercises (6-8), find the equation of the tangent line to each of the given functions at the indicated values of $x$. Then use a calculator to graph both the function and the tangent line to ensure the equation for the tangent line is correct.

6. $f(x)=−\sin x, \,\,\, x=0$
7. $f(x)=1+ \cos x, \,\,\, x=\frac{3\pi}{2}$
8. $f(x)=x^2- \tan x, \,\,\, x=0$

For the following exercises (9-11), find $\frac{d^2 y}{dx^2}$ for the given functions.

9. $y=x \sin x- \cos x$
10. $y=x-\frac{1}{2} \sin x$
11. $y=2 \csc x$

For the following exercises (12-15), solve each problem.

12. Find all $x$ values on the graph of $f(x)=-3 \sin x \cos x$ where the tangent line is horizontal.
13. Let $f(x)= \cot x$. Determine the point(s) on the graph of $f$ for $0 < x < 2\pi$ where the tangent line is parallel to the line $y=-2x$.
14. Let the position of a swinging pendulum in simple harmonic motion be given by $s(t)=a \cos t+b \sin t$ where $a$ and $b$ are constants, $t$ measures time in seconds, and $s$ measures position in centimeters, If the position is $0$cm and the velocity is $3$cm/s when $t=0$, find the values of $a$ and $b$.
15. The number of hamburgers sold at a fast-food restaurant in Pasadena, California, is given by $y=10+5 \sin x$ where $y$ is the number of hamburgers sold and $x$ represents the number of hours after the restaurant opened at 11 a.m. until 11 p.m., when the store closes. Find $y^{\prime}$ and determine the intervals where the number of burgers being sold is increasing.

For the following exercises (16-18), find the requested higher-order derivative for the given functions.

16. $\frac{d^3 y}{dx^3}$ of $y=3 \cos x$
17. $\frac{d^4 y}{dx^4}$ of $y=5 \cos x$
18. $\frac{d^3 y}{dx^3}$ of $y=x^{10}- \sec x$

The Chain Rule

For the following exercises (1-3), given $y=f(u)$ and $u=g(x)$, find $\frac{dy}{dx}$ by using Leibniz’s notation for the chain rule: $\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$.

1. $y=6u^3, \,\,\, u=7x-4$
2. $y= \cos u, \,\,\, u=\dfrac{−x}{8}$
3. $y=\sqrt{4u+3}, \,\,\, u=x^2-6x$

For each of the following exercises (4-7),

1. decompose each function in the form $y=f(u)$ and $u=g(x)$, and
2. find $\frac{dy}{dx}$ as a function of $x$.

4. $y=(3x^2+1)^3$
5. $y=\left(\dfrac{x}{7}+\dfrac{7}{x}\right)^7$
6. $y= \csc (\pi x+1)$
7. $y=-6 \sin^{-3} x$

For the following exercises (8-12), find $\frac{dy}{dx}$ for each function.

8. $y=(5-2x)^{-2}$
9. $y=(2x^3-x^2+6x+1)^3$
10. $y=(\tan x+ \sin x)^{-3}$
11. $y= \sin (\cos 7x)$
12. $y= \cot^3 (4x+1)$

For the following exercises (13-16), use the information in the following table to find $h^{\prime}(a)$ at the given value for $a$.

$x$	$f(x)$	$f^{\prime}(x)$	$g(x)$	$g^{\prime}(x)$
$0$	$2$	$5$	$0$	$2$
$1$	$1$	$−2$	$3$	$0$
$2$	$4$	$4$	$1$	$−1$
$3$	$3$	$−3$	$2$	$3$

13. $h(x)=f(g(x)); \,\,\, a=0$
14. $h(x)=(x^4+g(x))^{-2}; \,\,\, a=1$
15. $h(x)=f(x+f(x)); \,\,\, a=1$
16. $h(x)=g(2+f(x^2)); \, a=1$

For the following exercises (17-23), solve each problem.

17. Let $y=(f(x)+5x^2)^4$ and suppose that $f(-1)=-4$ and $\frac{dy}{dx}=3$ when $x=-1$. Find $f^{\prime}(-1)$
18. Find the equation of the tangent line to $y=−\sin \left(\dfrac{x}{2}\right)$ at the origin. Use a calculator to graph the function and the tangent line together.
19. Find the $x$-coordinates at which the tangent line to $y=\left(x-\dfrac{6}{x}\right)^8$ is horizontal.
20. The position function of a freight train is given by $s(t)=100(t+1)^{-2}$, with $s$ in meters and $t$ in seconds. At time $t=6$ s, find the train’s
    1. velocity and
    2. acceleration.
    3. Using a. and b. is the train speeding up or slowing down?
21. The total cost to produce $x$ boxes of Thin Mint Girl Scout cookies is $C$ dollars, where $C=0.0001x^3-0.02x^2+3x+300$. In $t$ weeks production is estimated to be $x=1600+100t$ boxes.
    1. Find the marginal cost $C^{\prime}(x)$.
    2. Use Leibniz’s notation for the chain rule, $\frac{dC}{dt}=\frac{dC}{dx} \cdot \frac{dx}{dt}$, to find the rate with respect to time $t$ that the cost is changing.
    3. Use b. to determine how fast costs are increasing when $t=2$ weeks. Include units with the answer.
22. The formula for the volume of a sphere is $S=\frac{4}{3}\pi r^3$, where $r$ (in feet) is the radius of the sphere. Suppose a spherical snowball is melting in the sun.
    1. Suppose $r=\dfrac{1}{(t+1)^2}-\dfrac{1}{12}$ where $t$ is time in minutes. Use the chain rule $\frac{dS}{dt}=\frac{dS}{dr} \cdot \frac{dr}{dt}$ to find the rate at which the snowball is melting.
    2. Use a. to find the rate at which the volume is changing at $t=1$ min.
23. The depth (in feet) of water at a dock changes with the rise and fall of tides. The depth is modeled by the function $D(t)=5 \sin \left(\dfrac{\pi}{6} t-\dfrac{7\pi}{6}\right)+8$, where $t$ is the number of hours after midnight. Find the rate at which the depth is changing at 6 a.m.

Derivatives of Inverse Functions

For the following exercises (1-2), use the graph of $y=f(x)$ to

1. sketch the graph of $y=f^{-1}(x)$, and
2. use part (a) to estimate $(f^{-1})^{\prime}(1)$.

1. 
2. 

For the following exercises (3-4), use the functions $y=f(x)$ to find

1. $\frac{df}{dx}$ at $x=a$ and
2. $x=f^{-1}(y)$.
3. Then use part (b) to find $\frac{df^{-1}}{dy}$ at $y=f(a)$.

3. $f(x)=2x^3-3, \,\,\ x=1$
4. $f(x)= \sin x, \,\,\ x=0$

For each of the following functions (5-7), find $(f^{-1})^{\prime}(a)$.

5. $f(x)=x^3+2x+3, \,\,\ a=0$
6. $f(x)=x-\dfrac{2}{x}, \,\,\ x<0, \,\,\ a=1$
7. $f(x)= \tan x+3x^2, \,\,\ a=0$

For each of the given functions (8-9) $y=f(x)$,

1. find the slope of the tangent line to its inverse function $f^{-1}$ at the indicated point $P$, and
2. find the equation of the tangent line to the graph of $f^{-1}$ at the indicated point.

8. $f(x)=\sqrt{x-4}, \,\,\ P(2,8)$
9. $f(x)=−x^3-x+2, \,\,\ P(-8,2)$

For the following exercises (10-14), find $\frac{dy}{dx}$ for the given function.

10. $y= \sin^{-1}(x^2)$
11. $y= \sec^{-1}\left(\dfrac{1}{x}\right)$
12. $y=(1 + \tan^{-1} x)^3$
13. $y=\dfrac{1}{\tan^{-1}(x)}$
14. $y= \cot^{-1} \sqrt{4-x^2}$

For the following exercises (15-17), use the given values to find $(f^{-1})^{\prime}(a)$.

15. $f(\pi)=0, \,\,\ f^{\prime}(\pi)=-1, \,\,\ a=0$
16. $f(\frac{1}{3})=-8, \,\,\ f^{\prime}(\frac{1}{3})=2, \,\,\ a=-8$
17. $f(1)=-3, \,\,\ f^{\prime}(1)=10, \,\,\ a=-3$

For the following exercises (18-20), complete all parts of each question. You may utilize calculators or any technological aids to facilitate your calculations.

18. The position of a moving hockey puck after $t$ seconds is $s(t)= \tan^{-1} t$ where $s$ is in meters.
    1. Find the velocity of the hockey puck at any time $t$.
    2. Find the acceleration of the puck at any time $t$.
    3. Evaluate a. and b. for $t=2,4$, and 6 seconds.
    4. What conclusion can be drawn from the results in c.?
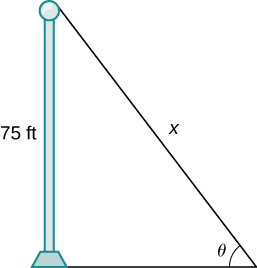
19. A pole stands 75 feet tall. An angle $\theta$ is formed when wires of various lengths of $x$ feet are attached from the ground to the top of the pole, as shown in the following figure. Find the rate of change of the angle $\frac{d\theta}{dx}$ when a wire of length 90 feet is attached.

    

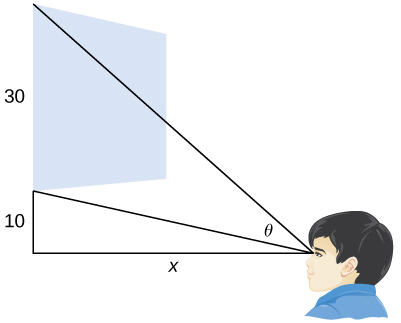
20. A local movie theater with a 30-foot-high screen that is 10 feet above a person’s eye level when seated has a viewing angle $\theta$ (in radians) given by $\theta = \cot^{-1}\left(\frac{x}{40}\right)- \cot^{-1}\left(\frac{x}{10}\right)$,

    where $x$ is the distance in feet away from the movie screen that the person is sitting, as shown in the following figure.

    

    1. Find $\frac{d\theta}{dx}$.
    2. Evaluate $\frac{d\theta}{dx}$ for $x=5,10,15$, and $20$.
    3. Interpret the results in b.
    4. Evaluate $\frac{d\theta}{dx}$ for $x=25,30,35$, and $40$
    5. Interpret the results in d. At what distance $x$ should the person sit to maximize his or her viewing angle?

Implicit Differentiation

For the following exercises (1-5), use implicit differentiation to find $\frac{dy}{dx}$.

1. $6x^2+3y^2=12$
2. $3x^3+9xy^2=5x^3$
3. $y\sqrt{x+4}=xy+8$
4. $y \sin(xy)=y^2+2$
5. $x^3 y+xy^3=-8$

For the following exercises (6-8), find the equation of the tangent line to the graph of the given equation at the indicated point. Use a calculator or computer software to graph the function and the tangent line.

6. $x^2 y^2+5xy=14, \,\,\, (2,1)$
7. $xy^2 + \sin(\pi y)-2x^2=10, \,\,\, (2,-3)$
8. $xy+ \sin (x)=1, \,\,\, (\frac{\pi}{2},0)$

For the following exercises (9-13), solve each problem.

9. For the equation $x^2+2xy-3y^2=0$,
   1. Find the equation of the normal to the tangent line at the point $(1,1)$.
   2. At what other point does the normal line in a. intersect the graph of the equation?
10. For the equation $x^2+xy+y^2=7$,
    1. Find the $x$-intercept(s).
    2. Find the slope of the tangent line(s) at the $x$-intercept(s).
    3. What does the value(s) in b. indicate about the tangent line(s)?
11. Find the equation of the tangent line to the graph of the equation $\tan^{-1}(x+y)=x^2+\frac{\pi}{4}$ at the point $(0,1)$.
12. The number of cell phones produced when $x$ dollars is spent on labor and $y$ dollars is spent on capital invested by a manufacturer can be modeled by the equation $60x^{\frac{3}{4}}y^{\frac{1}{4}}=3240$.
    1. Find $\frac{dy}{dx}$ and evaluate at the point $(81,16)$.
    2. Interpret the result of a.
13. The volume of a right circular cone of radius $x$ and height $y$ is given by $V=\frac{1}{3}\pi x^2 y$. Suppose that the volume of the cone is $85\pi \, \text{cm}^3$. Find $\frac{dy}{dx}$ when $x=4$ and $y=16$.

For the following exercise, consider a closed rectangular box with a square base with side $x$ and height $y$.

14. If the surface area of the rectangular box is $78$ square feet, find $\frac{dy}{dx}$ when $x=3$ feet and $y=5$ feet.

For the following exercise, use implicit differentiation to determine $y^{\prime}$. Does the answer agree with the formulas we have previously determined?

15. $x= \cos y$

Derivatives of Exponential and Logarithmic Functions

For the following exercises (1-8), find $f^{\prime}(x)$ for each function.

1. $f(x)=x^2 e^x$
2. $f(x)=e^{x^3 \ln x}$
3. $f(x)=\dfrac{e^x-e^{−x}}{e^x+e^{−x}}$
4. $f(x)=2^{4x}+4x^2$
5. $f(x)=x^{\pi} \cdot \pi^x$
6. $f(x)=\ln \sqrt{5x-7}$
7. $f(x)=\log(\sec x)$
8. $f(x)=2^x \cdot \log_3 7^{x^2-4}$

For the following exercises (9-12), use logarithmic differentiation to find $\frac{dy}{dx}$.

9. $y=(\sin 2x)^{4x}$
10. $y=x^{\log_2 x}$
11. $y=x^{\cot x}$
12. $y=x^{-\frac{1}{2}}(x^2+3)^{\frac{2}{3}}(3x-4)^4$

For the following exercises (13-16), solve each problem.

13. Find the equation of the line that is normal to the graph of $f(x)=x \cdot 5^x$ at the point where $x=1$. Graph both the function and the normal line.
14. Consider the function $y=x^{\frac{1}{x}}$ for $x>0$.
    1. Determine the points on the graph where the tangent line is horizontal.
    2. Determine the intervals where $y^{\prime}>0$ and those where $y^{\prime}<0$.
15. The population of Toledo, Ohio, in 2000 was approximately $500,000$. Assume the population is increasing at a rate of $5\%$ per year.
    1. Write the exponential function that relates the total population as a function of $t$.
    2. Use a. to determine the rate at which the population is increasing in $t$ years.
    3. Use b. to determine the rate at which the population is increasing in $10$ years.
16. The number of cases of influenza in New York City from the beginning of 1960 to the beginning of 1961 is modeled by the function

    $N(t)=5.3e^{0.093t^2-0.87t}, \, (0\le t\le 4)$,

    where $N(t)$ gives the number of cases (in thousands) and $t$ is measured in years, with $t=0$ corresponding to the beginning of 1960.

    1. Show work that evaluates $N(0)$ and $N(4)$. Briefly describe what these values indicate about the disease in New York City.
    2. Show work that evaluates $N^{\prime}(0)$ and $N^{\prime}(3)$. Briefly describe what these values indicate about the disease in New York City.

For the following exercises (17-20), use the population of New York City from 1790 to 1860, given in the following table.

New York City Population Over Time Source: http://en.wikipedia.org/wiki/Largest_cities_in_the_United_States_by_population_by_decade

Years since 1790	Population
$0$	$33,131$
$10$	$60,515$
$20$	$96,373$
$30$	$123,706$
$40$	$202,300$
$50$	$312,710$
$60$	$515,547$
$70$	$813,669$

17. Using a computer program or a calculator, fit a growth curve to the data of the form $p=ab^t$.
18. Using the exponential best fit for the data, write a table containing the derivatives evaluated at each year.
19. Using the exponential best fit for the data, write a table containing the second derivatives evaluated at each year.
20. Using the tables of first and second derivatives and the best fit, answer the following questions:
    1. Will the model be accurate in predicting the future population of New York City? Why or why not?
    2. Estimate the population in 2010. Was the prediction correct from a.?