Techniques for Differentiation: Background You’ll Need 2

Lumen Learning

Techniques for Differentiation: Background You’ll Need 2

Use different methods to combine and change functions

Combining and Composing Functions

In mathematics, we often build upon basic functions by combining them with operations such as addition and multiplication or by creating composite functions. This process forms new functions that can better describe and analyze complex relationships.

Combining Functions with Mathematical Operators

To combine functions using mathematical operators, we simply write the functions with the operator and simplify. Given two functions $f$ and $g,$ we can define four new functions:

\begin{array}{cccc} (f + g) (x) = f (x) + g (x) & Sum \\ (f - g) (x) = f (x) - g (x) & Difference \\ (f \cdot g) (x) = f (x) g (x) & Product \\ (\frac{f}{g}) (x) = \frac{f (x)}{g (x)} for g (x) \neq 0 & Quotient \end{array}

$\begin{array}{cccc}(f+g)(x)=f(x)+g(x)\hfill & & & \text{Sum}\hfill \\ (f-g)(x)=f(x)-g(x)\hfill & & & \text{Difference}\hfill \\ (f·g)(x)=f(x)g(x)\hfill & & & \text{Product}\hfill \\ \Big(\frac{f}{g}\Big)(x)=\frac{f(x)}{g(x)} \, \text{for} \, g(x)\ne 0\hfill & & & \text{Quotient}\hfill \end{array}$

Often these functions have more than one term, so when you perform operations on them you will need to remember how to work with polynomials.

When given multiple polynomials, you can simplify expressions by adding or subtracting them, ensuring you combine like terms and rearrange the resulting polynomial into standard form, which is organized by descending powers. Multiplying binomials requires a different approach. Use the FOIL method to multiply the first, outer, inner, and last terms, and then combine like terms in the resulting expression.

Here’s a concise recap of both processes:

Adding/Subtracting Polynomials:
1. Combine like terms.
2. When subtracting, distribute the negative sign across the second polynomial.
3. Rearrange and combine terms into standard form.

Be particularly cautious when subtracting polynomials to distribute the negative sign correctly.

Two quantities in parentheses are being multiplied, the first being: a times x plus b and the second being: c times x plus d. This expression equals ac times x squared plus ad times x plus bc times x plus bd. The terms ax and cx are labeled: First Terms. The terms ax and d are labeled: Outer Terms. The terms b and cx are labeled: Inner Terms. The terms b and d are labeled: Last Terms.

Multiplying Binomials (FOIL):
1. Multiply the first terms of each binomial.
2. Multiply the outer terms.
3. Multiply the inner terms.
4. Multiply the last terms.
5. Combine like terms and simplify the product.

Given the functions $f(x)=2x-3$ and $g(x)=x^2-1$ , find each of the following functions and state its domain.

$(f+g)(x)$
$(f-g)(x)$
$(f·g)(x)$
$\Big(\frac{f}{g}\Big)(x)$

$(f+g)(x)=(2x-3)+(x^2-1)=x^2+2x-4$ . The domain of this function is the interval $(−\infty ,\infty )$ .
$(f-g)(x)=(2x-3)-(x^2-1)=−x^2+2x-2$ . The domain of this function is the interval $(−\infty ,\infty)$ .
$(f·g)(x)=(2x-3)(x^2-1)=2x^3-3x^2-2x+3$ . The domain of this function is the interval $(−\infty ,\infty )$ .
$\Big(\frac{f}{g}\Big)(x)=\dfrac{2x-3}{x^2-1}$ . The domain of this function is $\{x|x\ne \text{±}1\}$ .

Watch the following video to see the worked solution to this example.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end. You can view the transcript for this segmented clip of “1.1 Review of Functions” using this link(opens in new window).

Composite Functions

Composite functions merge two functions into one by using the output of one function as the input of another.

For example, given the functions $f(x)=x^2$ and $g(x)=3x+1$ , the composite function $f\circ g$ is defined such that

(f \circ g) (x) = f (g (x)) = (g (x))^{2} = (3 x + 1)^{2}

$(f\circ g)(x)=f(g(x))=(g(x))^2=(3x+1)^2$

This composition is unique because $f\circ g$ is not the same as $g\circ f$ .

(g \circ f) (x) = g (f (x)) = 3 f (x) + 1 = 3 x^{2} + 1

$(g\circ f)(x)=g(f(x))=3f(x)+1=3x^2+1$

The order in which functions are composed matters

composite functions

A composite function, denoted as $f\circ g$ , is created when the output of one function, $g(x)$ , becomes the input for another, $f(x)$ . The resulting function $f(g(x))$ has the domain of $g$ and the range of $f$ , provided that the range of $g$ is contained within the domain of $f$ .

(f \circ g) (x) = f (g (x))

$(f\circ g)(x)=f(g(x))$

It is important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside.

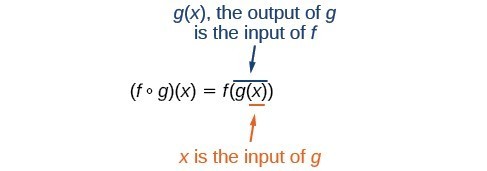
Explanation of the composite function. g(x), the output of g is the input of f. X is the input of g.

Consider the functions $f(x)=x^2+1$ and $g(x)=\frac{1}{x}$ .

Find $(f\circ g)(x)$ and state its domain and range.
Evaluate $(f\circ g)(4)$ and $(f\circ g)\left(-\frac{1}{2}\right)$ .

We can find a formula for $(f\circ g)(x)$ in two ways. First, we could write
$(f\circ g)(x)=f(g(x))=f\left(\frac{1}{x}\right)=\left(\frac{1}{x}\right)^2+1$

Alternatively, we could write

$(f\circ g)(x)=f(g(x))=(g(x))^2+1=\left(\frac{1}{x}\right)^2+1$

The domain of $f\circ g$ is the set of all real numbers $x$ such that $x\ne 0$ . To find the range of $f$ , we need to find all values $y$ for which there exists a real number $x\ne 0$ such that

$\left(\frac{1}{x}\right)^2+1=y$

Solving this equation for $x$ , we see that we need $x$ to satisfy

$\left(\frac{1}{x}\right)^2=y-1$ ,

which simplifies to

$\frac{1}{x}=±\sqrt{y-1}$

Finally, we obtain

$x=±\frac{1}{\sqrt{y-1}}$

Since $\frac{1}{\sqrt{y-1}}$ is a real number if and only if $y>1$ , the range of $f$ is the set $\{y|y\ge 1\}$ .
$(f\circ g)(4)=f(g(4))=f\left(\frac{1}{4}\right)=\left(\frac{1}{4}\right)^2+1=\frac{17}{16}$
$(f\circ g)\left(-\frac{1}{2}\right)=f\left(g\left(-\frac{1}{2}\right)\right)=f(-2)=(-2)^2+1=5$

Remember that $(f\circ g)(x)\ne (g\circ f)(x)$ .

Consider the functions $f$ and $g$ described below.

$x$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$
$f(x)$	$0$	$4$	$2$	$4$	$-2$	$0$	$-2$	$4$

$x$	$-4$	$-2$	$0$	$2$	$4$
$g(x)$	$1$	$0$	$3$	$0$	$5$

Evaluate $(g\circ f)(3)$ and $(g\circ f)(0)$ .
State the domain and range of $(g\circ f)(x)$ .

$(g\circ f)(3)=g(f(3))=g(-2)=0$
$(g\circ f)(0)=g(4)=5$
The domain of $g\circ f$ is the set $\{-3,-2,-1,0,1,2,3,4\}$ . Since the range of $f$ is the set $\{-2,0,2,4\}$ , the range of $g\circ f$ is the set $\{0,3,5\}$ .

A store is advertising a sale of $20\%$ off all merchandise. Caroline has a coupon that entitles her to an additional $15\%$ off any item, including sale merchandise. If Caroline decides to purchase an item with an original price of $x$ dollars, how much will she end up paying if she applies her coupon to the sale price? Solve this problem by using a composite function.

Since the sale price is $20\%$ off the original price, if an item is $x$ dollars, its sale price is given by $f(x)=0.80x$ . Since the coupon entitles an individual to $15\%$ off the price of any item, if an item is $y$ dollars, the price, after applying the coupon, is given by $g(y)=0.85y$ . Therefore, if the price is originally $x$ dollars, its sale price will be $f(x)=0.80x$ and then its final price after the coupon will be $g(f(x))=0.85(0.80x)=0.68x$ .