Symmetry

Symmetry, in its simplest form, refers to a sense of harmonious and aesthetically pleasing proportionality and balance. It’s a principle that is deeply rooted in nature, mathematics, art, design, and architecture. The basic idea behind symmetry is that if you were to draw a line through an object, shape, or design, one side would be a mirror image of the other.

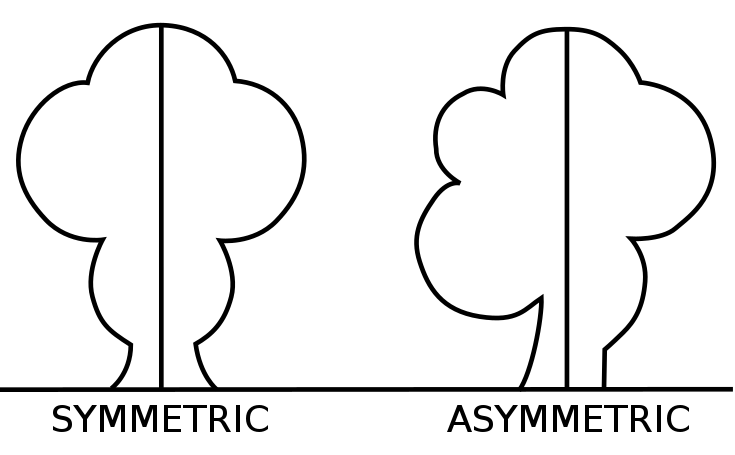
The line or plane that divides the shape, object or design into two equal and mirrored halves is called the axis of symmetry. This axis can be vertical, horizontal, or diagonal, depending on the orientation of the symmetrical shape.

In visual arts, symmetry is used to create a sense of balance and harmony within a composition. Symmetrical compositions can be calming and stable, often conveying a sense of order and perfection.

However, perfectly symmetrical compositions can also risk being seen as static or boring, which is why artists often balance symmetry with elements of asymmetry to create interest and dynamism. Breaking symmetry, while maintaining balance, can create visual interest and help guide the viewer’s eye to a focal point. This is often used in visual arts and design to create tension, emphasize certain elements, or convey movement and change.

There are three primary types of symmetry – reflection, rotation, and translation symmetry – which are often used in different combinations to create aesthetically pleasing and balanced designs.

reflection symmetry

Reflection symmetry, also known as mirror or bilateral symmetry, occurs when one half of an image, shape or design is the mirror image of the other half. That is, one side reflects the other.

 

Figures with the axes of symmetry drawn in. The figure with no axes is asymmetric.

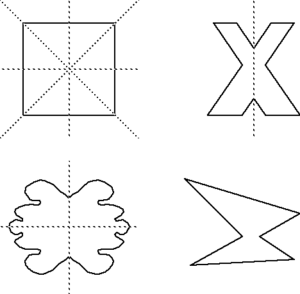
Reflection symmetry is common in architecture and design, as it imparts a sense of balance and harmony. Artists may also use it to create emphasis on a particular aspect of their work. For instance, think of a butterfly. The right wing is a mirror image of the left wing, hence it has reflection symmetry. In architecture, many buildings and structures – from the Taj Mahal to modern skyscrapers – feature reflection symmetry.

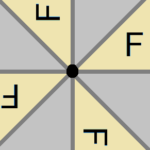
This type of symmetry is common in nature, such as in flowers and snowflakes, and is often used in design and art to create patterns that convey movement and dynamism.

translation symmetry

Translation symmetry, also known as slide symmetry, involves an image or design being repeated in a straight line. It’s like moving, or translating, an object without changing its orientation.

 

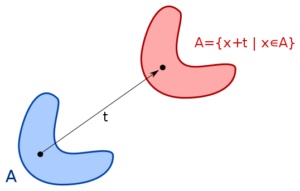
This type of symmetry is commonly used in wallpaper designs, textiles, and other works of art that involve repeated patterns.