Hydrostatic Force and Pressure

Let’s examine the force and pressure exerted on an object submerged in a liquid. Force is measured in newtons (metric) or pounds (English), and pressure is force per unit area, measured in pascals (metric) or psi (English).

Let’s begin with the simple case of a plate of area [latex]A[/latex] submerged horizontally in water at a depth [latex]s[/latex] (Figure 9). 

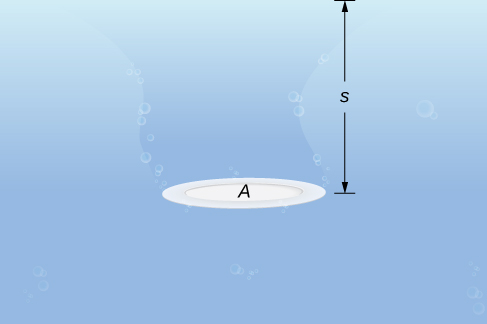
The force exerted on the plate is simply the weight of the water above it, which is given by [latex]F=\rho As,[/latex] where [latex]\rho[/latex] is the weight density of water (weight per unit volume).

To find the hydrostatic pressure—that is, the pressure exerted by water on a submerged object—we divide the force by the area. So the pressure is

[latex]p=\frac{F}{A}=\rho s.[/latex]

By Pascal’s principle, the pressure at a given depth is the same in all directions, so it does not matter if the plate is submerged horizontally or vertically. So, as long as we know the depth, we know the pressure. We can apply Pascal’s principle to find the force exerted on surfaces, such as dams, that are oriented vertically.

We cannot apply the formula [latex]F=\rho As[/latex] directly, because the depth varies from point to point on a vertically oriented surface. So, as we have done many times before, we form a partition, a Riemann sum, and, ultimately, a definite integral to calculate the force.

Suppose a thin plate is submerged in water. 

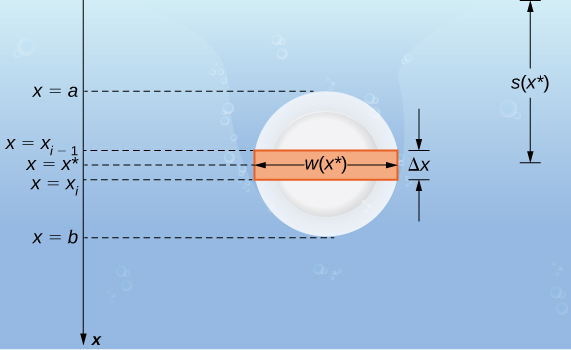
We choose our frame of reference such that the [latex]x[/latex]-axis is oriented vertically, with [latex]x=0[/latex] at the water’s surface. The depth at any point [latex]x[/latex] is given by [latex]s(x)=x[/latex]. The width of the plate at point [latex]x[/latex] is denoted by [latex]w(x)[/latex].

We partition the interval [latex][a,b][/latex] into [latex]n[/latex] segments. For each segment, we calculate the force using a Riemann sum and ultimately integrate to find the total force on the submerged surface.

To estimate the force on a representative segment of the submerged plate, we treat the segment as if it is at a constant depth [latex]s({x}_{i}^{*})[/latex]. The force on each segment is given by:

[latex]{F}_{i}=\rho As=\rho \left[w({x}_{i}^{*})\text{Δ}x\right]s({x}_{i}^{*})[/latex]

Adding the forces, we get an estimate for the force on the plate:

[latex]F\approx \underset{i=1}{\overset{n}{\text{∑}}}{F}_{i}=\underset{i=1}{\overset{n}{\text{∑}}}\rho \left[w({x}_{i}^{*})\text{Δ}x\right]s({x}_{i}^{*})[/latex]

This is a Riemann sum, so taking the limit as [latex]n→∞[/latex] gives us the exact force:

[latex]F=\underset{n\to \infty }{\text{lim}}\underset{i=1}{\overset{n}{\text{∑}}}\rho \left[w({x}_{i}^{*})\text{Δ}x\right]s({x}_{i}^{*})={\displaystyle\int }_{a}^{b}\rho w(x)s(x)dx[/latex]

Evaluating this integral provides the total force on the plate.

We summarize this in the following problem-solving strategy.

A water trough [latex]15[/latex] ft long has ends shaped like inverted isosceles triangles, with base [latex]8[/latex] ft and height [latex]3[/latex] ft. Find the force on one end of the trough if the trough is full of water.

Show Solution

Select a frame of reference with the [latex]x\text{-axis}[/latex] oriented vertically and the downward direction being positive. Select the top of the trough as the point corresponding to [latex]x=0[/latex] (step 1).

The depth function, then, is [latex]s(x)=x.[/latex] Using similar triangles, we see that [latex]w(x)=8-(8\text{/}3)x[/latex] (step 2).

Now, the weight density of water is [latex]62.4 lb/ft^3[/latex] (step 3), so applying the force equation from above, we obtain,

[latex]\begin{array}{cc}\hfill F& ={\displaystyle\int }_{a}^{b}\rho w(x)s(x)dx\hfill \\ & ={\displaystyle\int }_{0}^{3}62.4(8-\frac{8}{3}x)xdx=62.4{\displaystyle\int }_{0}^{3}(8x-\frac{8}{3}{x}^{2})dx\hfill \\ & =62.4{\left[4{x}^{2}-\frac{8}{9}{x}^{3}\right]|}_{0}^{3}=748.8.\hfill \end{array}[/latex]

The water exerts a force of [latex]748.8[/latex] lb on the end of the trough (step 4).

Understanding the principles of hydrostatic force and pressure is crucial in real-world applications, such as the design and construction of large structures like the Hoover Dam. The Hoover Dam holds back massive volumes of water, requiring precise calculations of pressure and force to ensure stability and safety.

To learn more about Hoover Dam, visit this article published by the History Channel.