Physical Applications: Learn It 3

Work Done by a Force

In physics, work is related to force, which is often intuitively defined as a push or pull on an object. When a force moves an object, we say the force does work on the object.

In other words, work can be thought of as the amount of energy it takes to move an object.

The unit of force is the newton ([latex]N[/latex]), and work is measured in joules ([latex]J[/latex]).

When the force is constant, calculating work is straightforward.. According to physics, when we have a constant force, work can be expressed as the product of force and distance. It is rare, however, for a force to be constant. 

However, when the force varies, we need to partition the interval [latex][a,b][/latex] into [latex]n[/latex] segments. For a variable force [latex]F(x)[/latex], the work done over each subinterval can be approximated as:

[latex]{W}_{i}\approx F({x}_{i}^{*})({x}_{i}-{x}_{i-1})=F({x}_{i}^{*})\text{Δ}x.[/latex]

 

Summing the work done over all segments gives:

[latex]W=\displaystyle\sum_{i=1}^{n} {W}_{i}\approx \displaystyle\sum_{i=1}^{n} F({x}_{i}^{*})\text{Δ}x.[/latex]

 

Taking the limit as [latex]n\to \infty[/latex], we get the exact value for work:

[latex]W=\underset{n\to \infty }{\text{lim}} \displaystyle\sum_{i=1}^{n} F({x}_{i}^{*})\text{Δ}x={\displaystyle\int }_{a}^{b}F(x)dx.[/latex]

 

This integral provides the exact value of the work done by a varying force.

work done by a variable force

If a variable force [latex]F(x)[/latex] moves an object in a positive direction along the [latex]x[/latex]-axis from point [latex]a[/latex] to point [latex]b[/latex], then the work done on the object is

[latex]W={\displaystyle\int }_{a}^{b}F(x)dx[/latex]
If the force is constant, the integral evaluates to [latex]F·(b-a)=F·d.[/latex]

Consider a block attached to a horizontal spring. The block moves back and forth as the spring stretches and compresses. Although in the real world we would have to account for the force of friction between the block and the surface on which it is resting, we ignore friction here and assume the block is resting on a frictionless surface. 

When the spring is at its natural length (at rest), the system is said to be at equilibrium. In this state, the spring is neither elongated nor compressed, and in this equilibrium position the block does not move until some force is introduced. We orient the system such that [latex]x=0[/latex] corresponds to the equilibrium position.

"This

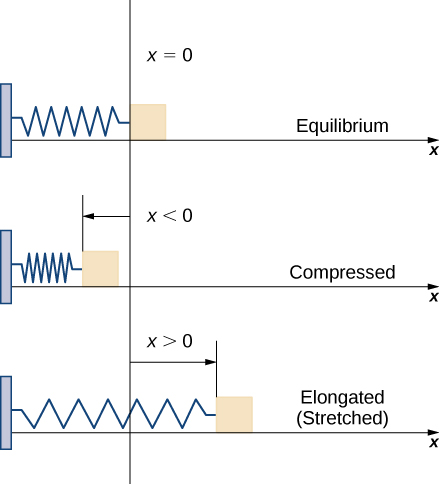
Spring Behavior:

  • [latex]x=0[/latex]: Equilibrium
  • [latex]x<0[/latex]: Compressed
  • [latex]x>o[/latex]: Stretched

According to Hooke’s law, the force required to compress or stretch the spring is [latex]F(x)=kx[/latex], where [latex]k[/latex] is the spring constant. The constant [latex]k[/latex] depends on the spring’s physical characteristics and is always positive. This information helps calculate the work done to compress or elongate the spring.

Suppose it takes a force of [latex]10[/latex] N (in the negative direction) to compress a spring [latex]0.2[/latex] m from the equilibrium position. How much work is done to stretch the spring [latex]0.5[/latex] m from the equilibrium position?