Approximating with Newton’s Method Cont.

Failures of Newton’s Method

Typically, Newton’s method is used to find roots fairly quickly. However, things can go wrong. Some reasons why Newton’s method might fail include the following:

1. At one of the approximations [latex]x_n[/latex], the derivative [latex]f^{\prime}[/latex] is zero at [latex]x_n[/latex], but [latex]f(x_n) \ne 0[/latex]. As a result, the tangent line of [latex]f[/latex] at [latex]x_n[/latex] does not intersect the [latex]x[/latex]-axis. Therefore, we cannot continue the iterative process.
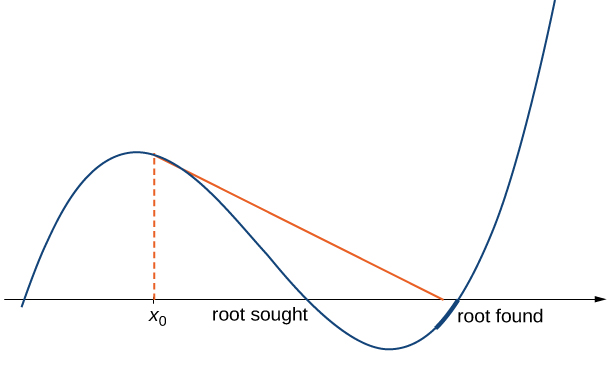
2. The approximations [latex]x_0,x_1,x_2, \cdots[/latex] may approach a different root. If the function [latex]f[/latex] has more than one root, it is possible that our approximations do not approach the one for which we are looking, but approach a different root (see Figure 4). This event most often occurs when we do not choose the approximation [latex]x_0[/latex] close enough to the desired root.
3. The approximations may fail to approach a root entirely. In the example below, we provide an example of a function and an initial guess [latex]x_0[/latex] such that the successive approximations never approach a root because the successive approximations continue to alternate back and forth between two values.

Consider the function [latex]f(x)=x^3-2x+2[/latex]. Let [latex]x_0=0[/latex]. Show that the sequence [latex]x_1,x_2, \cdots[/latex] fails to approach a root of [latex]f[/latex].

Show Solution

For [latex]f(x)=x^3-2x+2[/latex], the derivative is [latex]f^{\prime}(x)=3x^2-2[/latex]. Therefore,

[latex]x_1=x_0-\frac{f(x_0)}{f^{\prime}(x_0)}=0-\frac{f(0)}{f^{\prime}(0)}=-\frac{2}{-2}=1[/latex].

In the next step,

[latex]x_2=x_1-\frac{f(x_1)}{f^{\prime}(x_1)}=1-\frac{f(1)}{f^{\prime}(1)}=1-\frac{1}{1}=0[/latex].

Consequently, the numbers [latex]x_0,x_1,x_2, \cdots[/latex] continue to bounce back and forth between 0 and 1 and never get closer to the root of [latex]f[/latex] which is over the interval [latex][-2,-1][/latex] (see Figure 5). Fortunately, if we choose an initial approximation [latex]x_0[/latex] closer to the actual root, we can avoid this situation.

Watch the following video to see the worked solution to this example.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “4.9 Newton’s Method” here (opens in new window).

From the example above, we see that Newton’s method does not always work. However, when it does work, the sequence of approximations approaches the root very quickly. Discussions of how quickly the sequence of approximations approach a root found using Newton’s method are included in texts on numerical analysis.