Moments and Centers of Mass: Learn It 2

Lumen Learning

Moments and Centers of Mass: Learn It 2

Center of Mass of Thin Plates

We’ve examined point masses on a line and in a plane. Now, we look at systems where mass is distributed continuously across a thin sheet, called a lamina. We assume the lamina’s density is constant.

Laminas are often two-dimensional regions in a plane, with the geometric center called its centroid. The center of mass of a lamina depends only on the shape, not the density. For a rectangular lamina, the center of mass is where the diagonals intersect, which follows the symmetry principle.

the symmetry principle

If a region $R$ is symmetric about a line $l$ , then the centroid of $R$ lies on $l$ .

Let’s examine general laminas. Suppose we have a lamina bounded above by the graph of a continuous function $f(x),$ below by the $x$ -axis, and on the left and right by the lines $x=a$ and $x=b,$ .

This image is a graph of y=f(x). It is in the first quadrant. Under the curve is a shaded region labeled “R”. The shaded region is bounded to the left at x=a and to the right at x=b. — Figure 4. A region in the plane representing a lamina.

To find the center of mass, we need the total mass of the lamina. We divide the lamina into thin vertical strips, approximating each strip’s mass using the density $ρ$ . The mass of the strip is given by $\rho f({x}_{i}^{*})\text{Δ}x.$

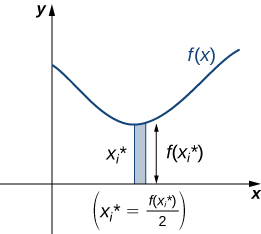
This figure is a graph of the curve labeled f(x). It is in the first quadrant. Under the curve and above the x-axis there is a vertical shaded rectangle. the height of the rectangle is labeled f(xsubi). Also, xsubi = f(xsubi/2). — Figure 5. A representative rectangle of the lamina.

To get the approximate mass of the lamina, we add the masses of all the rectangles to get

m \approx \underset{i = 1}{∑^{n}} ρ f (x_{i}^{*}) Δ x

$m\approx \underset{i=1}{\overset{n}{\text{∑}}}\rho f({x}_{i}^{*})\text{Δ}x$

This is a Riemann sum. Taking the limit as $n\to \infty$ gives the exact mass of the lamina:

m = lim_{n \to \infty} \underset{i = 1}{∑^{n}} ρ f (x_{i}^{*}) Δ x = ρ \int_{a}^{b} f (x) d x

$m=\underset{n\to \infty }{\text{lim}}\underset{i=1}{\overset{n}{\text{∑}}}\rho f({x}_{i}^{*})\text{Δ}x=\rho {\displaystyle\int }_{a}^{b}f(x)dx$

Next, we calculate the moment of the lamina with respect to the x-axis. For each rectangle, the center of mass is at $x_{i}^{*}$ . The moment with respect to the $x$ -axis is given by:

M_{x} = lim_{n \to \infty} \underset{i = 1}{∑^{n}} ρ \frac{{[f (x_{i}^{*})]}^{2}}{2} Δ x = ρ \int_{a}^{b} \frac{{[f (x)]}^{2}}{2} d x .

${M}_{x}=\underset{n\to \infty }{\text{lim}}\underset{i=1}{\overset{n}{\text{∑}}}\rho \frac{{\left[f({x}_{i}^{*})\right]}^{2}}{2}\text{Δ}x=\rho {\displaystyle\int }_{a}^{b}\frac{{\left[f(x)\right]}^{2}}{2}dx.$

Similarly, the moment with respect to the $y$ -axis is:

M_{y} = lim_{n \to \infty} \underset{i = 1}{∑^{n}} ρ x_{i}^{*} f (x_{i}^{*}) Δ x = ρ \int_{a}^{b} x f (x) d x

${M}_{y}=\underset{n\to \infty }{\text{lim}}\underset{i=1}{\overset{n}{\text{∑}}}\rho {x}_{i}^{*}f({x}_{i}^{*})\text{Δ}x=\rho {\displaystyle\int }_{a}^{b}xf(x)dx$

The coordinates of the center of mass are:

$\overline{x}=\frac{{M}_{y}}{m} \text{ and }\overline{y}=\frac{{M}_{x}}{m}$

If we look closely at the expressions for ${M}_{x},{M}_{y},\text{ and }m,$ we notice that the constant $\rho$ cancels out when $\overline{x}$ and $\overline{y}$ are calculated.

We summarize these findings in the following theorem.

center of mass of a thin plate in the $xy$ -plane

Let $R$ denote a region bounded above by the graph of a continuous function $f(x),$ below by the $x$ -axis, and on the left and right by the lines $x=a$ and $x=b,$ respectively. Let $\rho$ denote the density of the associated lamina. Then we can make the following statements:

The mass of the lamina is
$m=\rho {\displaystyle\int }_{a}^{b}f(x)dx.$
The moments ${M}_{x}$ and ${M}_{y}$ of the lamina with respect to the $x$ – and $y$ -axes, respectively, are
${M}_{x}=\rho {\displaystyle\int }_{a}^{b}\frac{{\left[f(x)\right]}^{2}}{2}dx\text{ and }{M}_{y}=\rho {\displaystyle\int }_{a}^{b}xf(x)dx.$
The coordinates of the center of mass $(\overline{x},\overline{y})$ are
$\overline{x}=\frac{{M}_{y}}{m}\text{ and }\overline{y}=\frac{{M}_{x}}{m}.$

In the next example, we use this theorem to find the center of mass of a lamina.

Let R be the region bounded above by the graph of the function $f(x)=\sqrt{x}$ and below by the $x$ -axis over the interval $\left[0,4\right].$ Find the centroid of the region.

The region is depicted in the following figure.

This figure is the graph of the curve f(x)=squareroot(x). It is an increasing curve in the first quadrant. Under the curve above the x-axis there is a shaded region. It starts at x=0 and is bounded to the right at x=4. — Figure 6. Finding the center of mass of a lamina.

Since we are only asked for the centroid of the region, rather than the mass or moments of the associated lamina, we know the density constant $\rho$ cancels out of the calculations eventually. Therefore, for the sake of convenience, let’s assume $\rho =1.$

First, we need to calculate the total mass:

\begin{array}{cc} m & = ρ \int_{a}^{b} f (x) d x = \int_{0}^{4} \sqrt{x} d x \\ = {\frac{2}{3} x^{3 / 2} |}_{0}^{4} = \frac{2}{3} [8 - 0] = \frac{16}{3} . \end{array}

$\begin{array}{cc}\hfill m& =\rho {\displaystyle\int }_{a}^{b}f(x)dx={\displaystyle\int }_{0}^{4}\sqrt{x}dx\hfill \\ & ={\frac{2}{3}{x}^{3\text{/}2}|}_{0}^{4}=\frac{2}{3}\left[8-0\right]=\frac{16}{3}.\hfill \end{array}$

Next, we compute the moments:

\begin{array}{cc} M_{x} & = ρ \int_{a}^{b} \frac{{[f (x)]}^{2}}{2} d x \\ = \int_{0}^{4} \frac{x}{2} d x = {\frac{1}{4} x^{2} |}_{0}^{4} = 4 \end{array}

$\begin{array}{cc}\hfill {M}_{x}& =\rho {\displaystyle\int }_{a}^{b}\frac{{\left[f(x)\right]}^{2}}{2}dx\hfill \\ & ={\displaystyle\int }_{0}^{4}\frac{x}{2}dx={\frac{1}{4}{x}^{2}|}_{0}^{4}=4\hfill \end{array}$

and

\begin{array}{cc} M_{y} & = ρ \int_{a}^{b} x f (x) d x \\ = \int_{0}^{4} x \sqrt{x} d x = \int_{0}^{4} x^{3 / 2} d x \\ = {\frac{2}{5} x^{5 / 2} |}_{0}^{4} = \frac{2}{5} [32 - 0] = \frac{64}{5} . \end{array}

$\begin{array}{cc}\hfill {M}_{y}& =\rho {\displaystyle\int }_{a}^{b}xf(x)dx\hfill \\ & ={\displaystyle\int }_{0}^{4}x\sqrt{x}dx={\displaystyle\int }_{0}^{4}{x}^{3\text{/}2}dx\hfill \\ & ={\frac{2}{5}{x}^{5\text{/}2}|}_{0}^{4}=\frac{2}{5}\left[32-0\right]=\frac{64}{5}.\hfill \end{array}$

Thus, we have

\bar{x} = \frac{M_{y}}{m} = \frac{64 / 5}{16 / 3} = \frac{64}{5} \cdot \frac{3}{16} = \frac{12}{5} and \bar{y} = \frac{M_{x}}{y} = \frac{4}{16 / 3} = 4 \cdot \frac{3}{16} = \frac{3}{4} .

$\overline{x}=\frac{{M}_{y}}{m}=\frac{64\text{/}5}{16\text{/}3}=\frac{64}{5}·\frac{3}{16}=\frac{12}{5}\text{ and }\overline{y}=\frac{{M}_{x}}{y}=\frac{4}{16\text{/}3}=4·\frac{3}{16}=\frac{3}{4}.$

The centroid of the region is $(12\text{/}5,3\text{/}4).$

Moments and Centers of Mass: Learn It 2

Center of Mass of Thin Plates

the symmetry principle

center of mass of a thin plate in the xyxyxy-plane

center of mass of a thin plate in the $xy$ -plane