End Behavior Cont.

Determining End Behavior for Transcendental Functions

Trigonometric functions

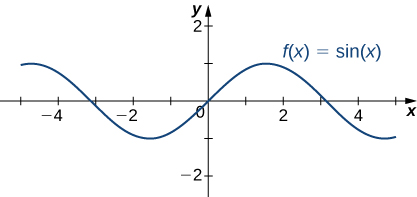
The six basic trigonometric functions are periodic and do not approach a finite limit as [latex]x\to \pm \infty[/latex].

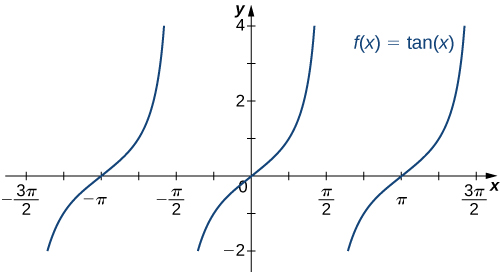
For example, [latex]\sin x[/latex] oscillates between 1 and -1 (Figure 19). The tangent function [latex]x[/latex] has an infinite number of vertical asymptotes as [latex]x\to \pm \infty[/latex]; therefore, it does not approach a finite limit nor does it approach [latex]\pm \infty[/latex] as [latex]x\to \pm \infty[/latex] as shown in (Figure 20).

Exponential functions

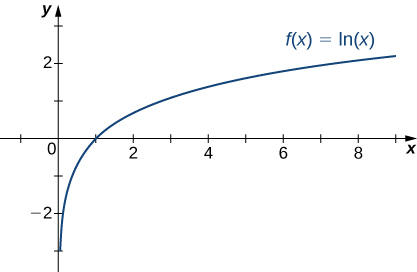
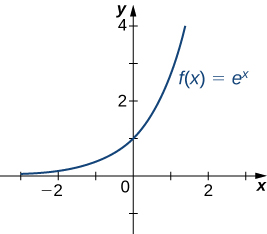
Recall that for any base [latex]b>0, \, b\ne 1[/latex], the function [latex]y=b^x[/latex] is an exponential function with domain [latex](−\infty ,\infty )[/latex] and range [latex](0,\infty )[/latex]. If [latex]b>1, \, y=b^x[/latex] is increasing over [latex](−\infty ,\infty )[/latex].If [latex]0

For the natural exponential function [latex]f(x)=e^x[/latex], [latex]e\approx 2.718>1[/latex]. Therefore, [latex]f(x)=e^x[/latex] is increasing on [latex](−\infty ,\infty )[/latex] and the range is [latex](0,\infty)[/latex]. The exponential function [latex]f(x)=e^x[/latex] approaches [latex]\infty[/latex] as [latex]x\to \infty[/latex] and approaches 0 as [latex]x\to −\infty[/latex].

Recall that the natural logarithm function [latex]f(x)=\ln (x)[/latex] is the inverse of the natural exponential function [latex]y=e^x[/latex]. Therefore, the domain of [latex]f(x)=\ln (x)[/latex] is [latex](0,\infty )[/latex] and the range is [latex](−\infty ,\infty )[/latex].

The graph of [latex]f(x)=\ln (x)[/latex] is the reflection of the graph of [latex]y=e^x[/latex] about the line [latex]y=x[/latex]. Therefore, [latex]\ln (x)\to −\infty[/latex] as [latex]x\to 0^+[/latex] and [latex]\ln (x)\to \infty[/latex] as [latex]x\to \infty[/latex].