Limits at Infinity Cont.
Formal Definitions
Earlier, we used the terms arbitrarily close, arbitrarily large, and sufficiently large to define limits at infinity informally. Although these terms provide accurate descriptions of limits at infinity, they are not precise mathematically.
Here are more formal definitions of limits at infinity.
limits at infinity (formal)
We say a function [latex]f[/latex] has a limit at infinity, if there exists a real number [latex]L[/latex] such that for all [latex]\varepsilon >0[/latex], there exists [latex]N>0[/latex] such that
for all [latex]x>N[/latex]. In that case, we write
We say a function [latex]f[/latex] has a limit at negative infinity if there exists a real number [latex]L[/latex] such that for all [latex]\varepsilon >0[/latex], there exists [latex]N<0[/latex] such that
for all [latex]x
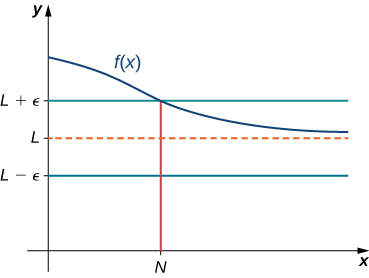
Earlier in this section, we used graphical evidence and numerical evidence to conclude that [latex]\underset{x\to \infty }{\lim}\left(2+\frac{1}{x}\right)=2[/latex]. Here we use the formal definition of limit at infinity to prove this result.
Use the formal definition of limit at infinity to prove that [latex]\underset{x\to \infty }{\lim}\left(2+\frac{1}{x}\right)=2[/latex].
We now turn our attention to a more precise definition for an infinite limit at infinity.
infinite limit at infinity (formal)
We say a function [latex]f[/latex] has an infinite limit at infinity and write
if for all [latex]M>0[/latex], there exists an [latex]N>0[/latex] such that
for all [latex]x>N[/latex].
We say a function has a negative infinite limit at infinity and write
if for all [latex]M<0[/latex], there exists an [latex]N>0[/latex] such that
for all [latex]x>N[/latex].
Similarly we can define limits as [latex]x\to −\infty[/latex].
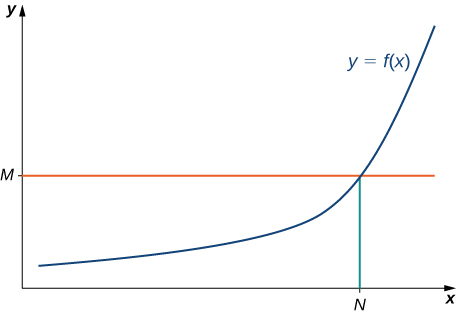
Earlier, we used graphical evidence and numerical evidence to conclude that [latex]\underset{x\to \infty }{\lim}x^3=\infty[/latex]. Here we use the formal definition of infinite limit at infinity to prove that result.
Use the formal definition of infinite limit at infinity to prove that [latex]\underset{x\to \infty }{\lim}x^3=\infty[/latex].