Limits at Infinity

We have shown how to use the first and second derivatives of a function to describe the shape of a graph. To graph a function [latex]f[/latex] defined on an unbounded domain, we also need to know the behavior of [latex]f[/latex] as [latex]x \to \pm \infty[/latex]. In this section, we define limits at infinity and show how these limits affect the graph of a function. At the end of this section, we outline a strategy for graphing an arbitrary function [latex]f[/latex].

We begin by examining what it means for a function to have a finite limit at infinity. Then we study the idea of a function with an infinite limit at infinity. We have looked at vertical asymptotes in other modules; in this section, we deal with horizontal and oblique asymptotes.

Limits at Infinity and Horizontal Asymptotes

Recall that [latex]\underset{x \to a}{\lim}f(x)=L[/latex] means [latex]f(x)[/latex] becomes arbitrarily close to [latex]L[/latex] as long as [latex]x[/latex] is sufficiently close to [latex]a[/latex]. We can extend this idea to limits at infinity.

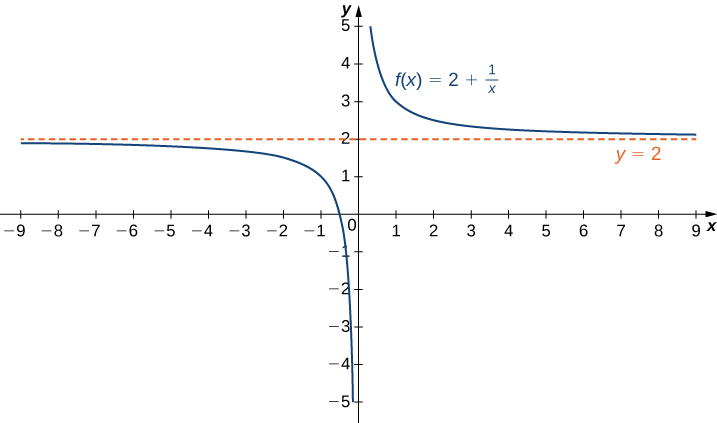
Consider the function [latex]f(x)=2+\frac{1}{x}[/latex].

As can be seen graphically in Figure 1 and numerically in the table beneath it, as the values of [latex]x[/latex] get larger, the values of [latex]f(x)[/latex] approach [latex]2[/latex]. We say the limit as [latex]x[/latex] approaches [latex]\infty[/latex] of [latex]f(x)[/latex] is [latex]2[/latex] and write:

[latex]\underset{x\to \infty }{\lim}f(x)=2[/latex].

Similarly, for [latex]x<0[/latex], as the values [latex]|x|[/latex] get larger, the values of [latex]f(x)[/latex] approaches [latex]2[/latex]. We say the limit as [latex]x[/latex] approaches [latex]−\infty[/latex] of [latex]f(x)[/latex] is [latex]2[/latex] and write:

[latex]\underset{x\to a}{\lim}f(x)=2[/latex].

Values of a function [latex]f[/latex] as [latex]x \to \pm \infty[/latex]

[latex]x[/latex]	[latex]10[/latex]	[latex]100[/latex]	[latex]1,000[/latex]	[latex]10,000[/latex]
[latex]2+\frac{1}{x}[/latex]	[latex]2.1[/latex]	[latex]2.01[/latex]	[latex]2.001[/latex]	[latex]2.0001[/latex]
[latex]x[/latex]	[latex]-10[/latex]	[latex]-100[/latex]	[latex]-1000[/latex]	[latex]-10,000[/latex]
[latex]2+\frac{1}{x}[/latex]	[latex]1.9[/latex]	[latex]1.99[/latex]	[latex]1.999[/latex]	[latex]1.9999[/latex]

More generally, for any function [latex]f[/latex], we say the limit as [latex]x \to \infty[/latex] of [latex]f(x)[/latex] is [latex]L[/latex] if [latex]f(x)[/latex] becomes arbitrarily close to [latex]L[/latex] as long as [latex]x[/latex] is sufficiently large. In that case, we write:

[latex]\underset{x\to \infty}{\lim}f(x)=L[/latex].

Similarly, we say the limit as [latex]x\to −\infty[/latex] of [latex]f(x)[/latex] is [latex]L[/latex] if [latex]f(x)[/latex] becomes arbitrarily close to [latex]L[/latex] as long as [latex]x<0[/latex] and [latex]|x|[/latex] is sufficiently large. In that case, we write:

[latex]\underset{x\to −\infty }{\lim}f(x)=L[/latex].

We now look at the definition of a function having a limit at infinity.

If the values [latex]f(x)[/latex] are getting arbitrarily close to some finite value [latex]L[/latex] as [latex]x\to \infty[/latex] or [latex]x\to −\infty[/latex], the graph of [latex]f[/latex] approaches the line [latex]y=L[/latex]. In that case, the line [latex]y=L[/latex] is a horizontal asymptote of [latex]f[/latex].

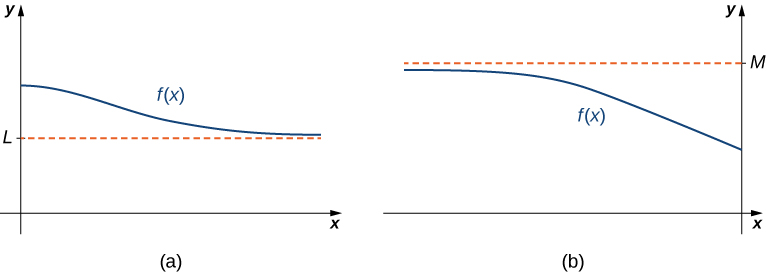
A function cannot cross a vertical asymptote because the graph must approach infinity (or negative infinity) from at least one direction as [latex]x[/latex] approaches the vertical asymptote. However, a function may cross a horizontal asymptote. In fact, a function may cross a horizontal asymptote an unlimited number of times.

The function [latex]f(x)=\frac{ \cos x}{x}+1[/latex] shown below intersects the horizontal asymptote [latex]y=1[/latex] an infinite number of times as it oscillates around the asymptote with ever-decreasing amplitude.

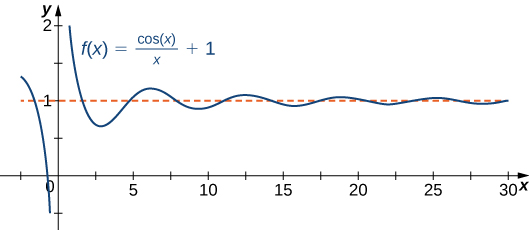
The algebraic limit laws and squeeze theorem we introduced earlier also apply to limits at infinity. We illustrate how to use these laws to compute several limits at infinity.

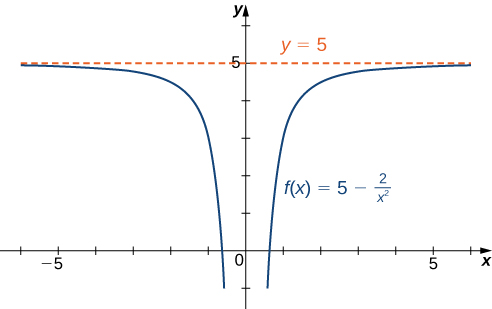
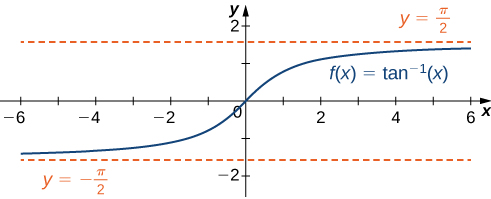
For each of the following functions [latex]f[/latex], evaluate [latex]\underset{x\to \infty }{\lim}f(x)[/latex] and [latex]\underset{x\to −\infty }{\lim}f(x)[/latex]. Determine the horizontal asymptote(s) for [latex]f[/latex].

1. [latex]f(x)=5-\frac{2}{x^2}[/latex]
2. [latex]f(x)=\dfrac{\sin x}{x}[/latex]
3. [latex]f(x)= \tan^{-1} (x)[/latex]

Show Solution

1. Using the algebraic limit laws, we have:
   [latex]\underset{x\to \infty }{\lim}(5-\frac{2}{x^2})=\underset{x\to \infty }{\lim}5-2(\underset{x\to \infty }{\lim}\frac{1}{x})(\underset{x\to \infty }{\lim}\frac{1}{x})=5-2 \cdot 0=5[/latex].

   Similarly, [latex]\underset{x\to -\infty }{\lim}f(x)=5[/latex]. Therefore, [latex]f(x)=5-\frac{2}{x^2}[/latex] has a horizontal asymptote of [latex]y=5[/latex] and [latex]f[/latex] approaches this horizontal asymptote as [latex]x\to \pm \infty[/latex] as shown in the following graph.

   

2. Since [latex]-1\le \sin x\le 1[/latex] for all [latex]x[/latex], we have:
   [latex]\frac{-1}{x}\le \frac{\sin x}{x}\le \frac{1}{x}[/latex]

   for all [latex]x \ne 0[/latex]. Also, since,

   [latex]\underset{x\to \infty }{\lim}\frac{-1}{x}=0=\underset{x\to \infty }{\lim}\frac{1}{x}[/latex],

   we can apply the squeeze theorem to conclude that:

   [latex]\underset{x\to \infty }{\lim}\frac{\sin x}{x}=0[/latex]

   Similarly,

   [latex]\underset{x\to −\infty}{\lim}\frac{\sin x}{x}=0[/latex]

    

   Thus, [latex]f(x)=\frac{\sin x}{x}[/latex] has a horizontal asymptote of [latex]y=0[/latex] and [latex]f(x)[/latex] approaches this horizontal asymptote as [latex]x\to \pm \infty[/latex] as shown in the following graph.

   

3. To evaluate [latex]\underset{x\to \infty }{\lim} \tan^{-1} (x)[/latex] and [latex]\underset{x\to −\infty}{\lim} \tan^{-1} (x)[/latex], we first consider the graph of [latex]y= \tan (x)[/latex] over the interval [latex](−\pi /2,\pi /2)[/latex] as shown in the following graph.
   

   

Since [latex]\underset{x\to (\pi/2)^-}{\lim} \tan x=\infty[/latex], it follows that:

[latex]\underset{x\to \infty }{\lim} \tan^{-1} (x)=\frac{\pi }{2}[/latex]

Similarly, since [latex]\underset{x\to (\pi/2)^+}{\lim} \tan x=−\infty[/latex], it follows that:

[latex]\underset{x\to −\infty}{\lim} \tan^{-1} (x)=-\frac{\pi }{2}[/latex]

As a result, [latex]y=\frac{\pi }{2}[/latex] and [latex]y=-\frac{\pi }{2}[/latex] are horizontal asymptotes of [latex]f(x)= \tan^{-1} (x)[/latex] as shown in the following graph.

Watch the following video to see the worked solution to this example.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “4.6 Limits at Infinity and Asymptotes” here (opens in new window).

Infinite Limits at Infinity

Sometimes the values of a function [latex]f[/latex] become arbitrarily large as [latex]x\to \infty[/latex] (or as [latex]x\to −\infty )[/latex]. In this case, we write [latex]\underset{x\to \infty }{\lim}f(x)=\infty[/latex] (or [latex]\underset{x\to −\infty }{\lim}f(x)=\infty )[/latex].

On the other hand, if the values of [latex]f[/latex] are negative but become arbitrarily large in magnitude as [latex]x\to \infty[/latex] (or as [latex]x\to −\infty )[/latex], we write [latex]\underset{x\to \infty }{\lim}f(x)=−\infty[/latex] (or [latex]\underset{x\to −\infty }{\lim}f(x)=−\infty )[/latex].

Consider the function [latex]f(x)=x^3[/latex].

Values of a power function as [latex]x\to \pm \infty[/latex]

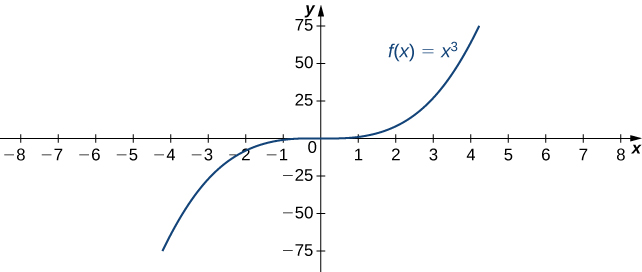
[latex]x[/latex]	[latex]10[/latex]	[latex]20[/latex]	[latex]50[/latex]	[latex]100[/latex]	[latex]1000[/latex]
[latex]x^3[/latex]	[latex]1000[/latex]	[latex]8000[/latex]	[latex]125,000[/latex]	[latex]1,000,000[/latex]	[latex]1,000,000,000[/latex]
[latex]x[/latex]	[latex]-10[/latex]	[latex]-20[/latex]	[latex]-50[/latex]	[latex]-100[/latex]	[latex]-1000[/latex]
[latex]x^3[/latex]	[latex]-1000[/latex]	[latex]-8000[/latex]	[latex]-125,000[/latex]	[latex]-1,000,000[/latex]	[latex]-1,000,000,000[/latex]

As seen in the table and figure above, as [latex]x\to \infty[/latex] the values [latex]f(x)[/latex] become arbitrarily large. Therefore, [latex]\underset{x\to \infty }{\lim}x^3=\infty[/latex].

On the other hand, as [latex]x\to −\infty[/latex], the values of [latex]f(x)=x^3[/latex] are negative but become arbitrarily large in magnitude. Consequently, [latex]\underset{x\to −\infty }{\lim}x^3=−\infty[/latex].