Limits and Continuity: Get Stronger

The Limit Laws

In the following exercises (1-2), use the limit laws to evaluate each limit. Justify each step by indicating the appropriate limit law(s).

  1. [latex]\underset{x\to 0}{\lim}(4x^2-2x+3)[/latex]
  2. [latex]\underset{x\to -2}{\lim}\sqrt{x^2-6x+3}[/latex]

In the following exercises (3-5), use direct substitution to evaluate each limit.

  1. [latex]\underset{x\to 7}{\lim}x^2[/latex]
  2. [latex]\underset{x\to 0}{\lim}\dfrac{1}{1+ \sin x}[/latex]
  3. [latex]\underset{x\to 1}{\lim}\dfrac{2-7x}{x+6}[/latex]

In the following exercises (6-10), use direct substitution to show that each limit leads to the indeterminate form [latex]\frac{0}{0}[/latex]. Then, evaluate the limit.

  1. [latex]\underset{x\to 4}{\lim}\dfrac{x^2-16}{x-4}[/latex]
  2. [latex]\underset{x\to 6}{\lim}\dfrac{3x-18}{2x-12}[/latex]
  3. [latex]\underset{t\to 9}{\lim}\dfrac{t-9}{\sqrt{t}-3}[/latex]
  4. [latex]\underset{\theta \to \pi}{\lim}\dfrac{\sin \theta}{\tan \theta}[/latex]
     
  5. [latex]\underset{x\to 1/2}{\lim}\dfrac{2x^2+3x-2}{2x-1}[/latex]

In the following exercises (11-14), assume that [latex]\underset{x\to 6}{\lim}f(x)=4, \, \underset{x\to 6}{\lim}g(x)=9[/latex], and [latex]\underset{x\to 6}{\lim}h(x)=6[/latex]. Use these three facts and the limit laws to evaluate each limit.

  1. [latex]\underset{x\to 6}{\lim}2f(x)g(x)[/latex]
  2. [latex]\underset{x\to 6}{\lim}(f(x)+\frac{1}{3}g(x))[/latex]
  3. [latex]\underset{x\to 6}{\lim}\sqrt{g(x)-f(x)}[/latex]
  4. [latex]\underset{x\to 6}{\lim}[(x+1)\cdot f(x)][/latex]

In the following exercises (15-16), use a calculator to draw the graph of each piecewise-defined function and study the graph to evaluate the given limits.

  1. [latex]f(x)=\begin{cases} x^2, & x \le 3 \\ x+4, & x > 3 \end{cases}[/latex]
    1. [latex]\underset{x\to 3^-}{\lim}f(x)[/latex]
    2. [latex]\underset{x\to 3^+}{\lim}f(x)[/latex]
  2. [latex]h(x)=\begin{cases} x^2-2x+1, & x < 2 \\ 3 - x, & x \ge 2 \end{cases}[/latex]
    1. [latex]\underset{x\to 2^-}{\lim}h(x)[/latex]
    2. [latex]\underset{x\to 2^+}{\lim}h(x)[/latex]

In the following exercises (17-20), use the graphs below and the limit laws to evaluate each limit.

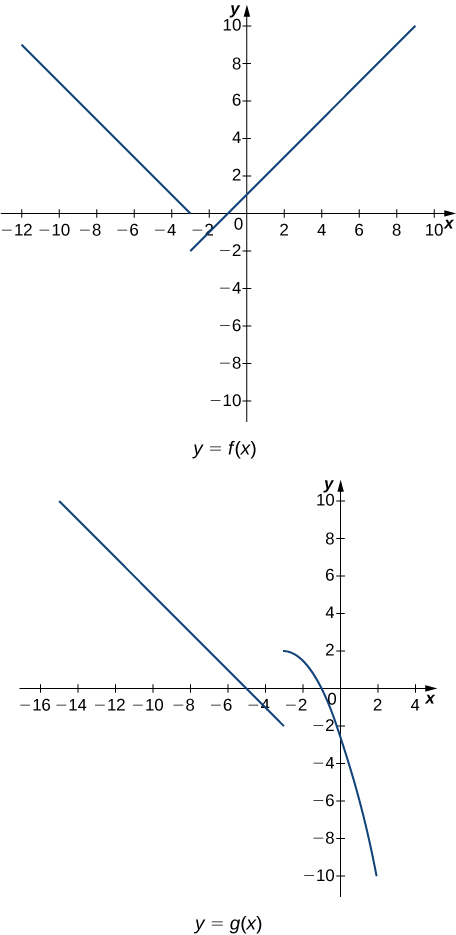
Two graphs of piecewise functions. The upper is f(x), which has two linear segments. The first is a line with negative slope existing for x < -3. It goes toward the point (-3,0) at x= -3. The next has increasing slope and goes to the point (-3,-2) at x=-3. It exists for x > -3. Other key points are (0, 1), (-5,2), (1,2), (-7, 4), and (-9,6). The lower piecewise function has a linear segment and a curved segment. The linear segment exists for x < -3 and has decreasing slope. It goes to (-3,-2) at x=-3. The curved segment appears to be the right half of a downward opening parabola. It goes to the vertex point (-3,2) at x=-3. It crosses the y axis a little below y=-2. Other key points are (0, -7/3), (-5,0), (1,-5), (-7, 2), and (-9, 4).

  1. [latex]\underset{x\to -3^-}{\lim}(f(x)-3g(x))[/latex]
  2. [latex]\underset{x\to -5}{\lim}\dfrac{2+g(x)}{f(x)}[/latex]
  3. [latex]\underset{x\to 1}{\lim}\sqrt[3]{f(x)-g(x)}[/latex]
  4. [latex]\underset{x\to -9}{\lim}[xf(x)+2g(x)][/latex]

Continuity

For the following exercises (1-4), determine the point(s), if any, at which each function is discontinuous. Classify any discontinuity as jump, removable, infinite, or other.

  1. [latex]f(x)=\dfrac{1}{\sqrt{x}}[/latex]
  2. [latex]f(x)=\dfrac{x}{x^2-x}[/latex]
  3. [latex]f(x)=\dfrac{5}{e^x-2}[/latex]
  4. [latex]H(x)= \tan 2x[/latex]

For the following exercises (5-7), decide if the function continuous at the given point. If it is discontinuous, what type of discontinuity is it?

  1. [latex]f(x)=\dfrac{2x^2-5x+3}{x-1}[/latex] at [latex]x=1[/latex]
  2. [latex]g(u)=\begin{cases} \dfrac{6u^2+u-2}{2u-1} & \text{ if } \, u \ne \frac{1}{2} \\ \dfrac{7}{2} & \text{ if } \, u = \frac{1}{2} \end{cases}[/latex] at [latex]u=\frac{1}{2}[/latex]
  3. [latex]f(x)=\begin{cases} x^2-e^x & \text{ if } \, x < 0 \\ x-1 & \text{ if } \, x \ge 0 \end{cases}[/latex] at [latex]x=0[/latex]

In the following exercises (8-10), find the value(s) of [latex]k[/latex] that makes each function continuous over the given interval.

  1. [latex]f(x)=\begin{cases} 3x+2 & \text{ if } \, x < k \\ 2x-3 & \text{ if } \, k \le x \le 8 \end{cases}[/latex]
  2. [latex]f(x)=\begin{cases} \dfrac{x^2+3x+2}{x+2} & \text{ if } \, x \ne -2 \\ k & \text{ if } \, x = -2 \end{cases}[/latex]
  3. [latex]f(x)=\begin{cases} \sqrt{kx} & \text{ if } \, 0 \le x \le 3 \\ x+1 & \text{ if } \, 3 < x \le 10 \end{cases}[/latex]

In the following exercises (11-12), sketch the graphs.

  1. Let [latex]f(x)=\begin{cases} 3x & \text{ if } \, x > 1 \\ x^3 & \text{ if } \, x < 1 \end{cases}[/latex]
    1. Sketch the graph of [latex]f[/latex].
    2. Is it possible to find a value [latex]k[/latex] such that [latex]f(1)=k[/latex], which makes [latex]f(x)[/latex] continuous for all real numbers? Briefly explain.
  2. Sketch the graph of the function [latex]y=f(x)[/latex] with properties 1 through 7.
    1. The domain of [latex]f[/latex] is [latex](−\infty,+\infty)[/latex].
    2. [latex]f[/latex] has an infinite discontinuity at [latex]x=-6[/latex].
    3. [latex]f(-6)=3[/latex]
    4. [latex]\underset{x\to -3^-}{\lim}f(x)=\underset{x\to -3^+}{\lim}f(x)=2[/latex]
    5. [latex]f(-3)=3[/latex]
    6. [latex]f[/latex] is left continuous but not right continuous at [latex]x=3[/latex].
    7. [latex]\underset{x\to -\infty}{\lim}f(x)=−\infty[/latex] and [latex]\underset{x\to +\infty}{\lim}f(x)=+\infty[/latex]

In the following exercise, suppose [latex]y=f(x)[/latex] is defined for all [latex]x[/latex]. For each description, sketch a graph with the indicated property.

  1. Discontinuous at [latex]x=1[/latex] with [latex]\underset{x\to -1}{\lim}f(x)=-1[/latex] and [latex]\underset{x\to 2}{\lim}f(x)=4[/latex]

Determine whether each of the given statements is true (14-17). Justify your responses with an explanation or counterexample.

  1. [latex]f(t)=\dfrac{2}{e^t-e^{-t}}[/latex] is continuous everywhere.
  2. If a function is not continuous at a point, then it is not defined at that point.
  3. If [latex]f(x)[/latex] is continuous such that [latex]f(a)[/latex] and [latex]f(b)[/latex] have opposite signs, then [latex]f(x)=0[/latex] has exactly one solution in [latex][a,b][/latex].
  4. If [latex]f(x)[/latex] is continuous everywhere and [latex]f(a), f(b)>0[/latex], then there is no root of [latex]f(x)[/latex] in the interval [latex][a,b][/latex].

Prove the following functions are continuous everywhere (18-19).

  1. [latex]f(\theta) = \sin \theta[/latex]
  2. Where is [latex]f(x)=\begin{cases} 0 & \text{ if } \, x \, \text{is irrational} \\ 1 & \text{ if } \, x \, \text{is rational} \end{cases}[/latex] continuous?

The Precise Definition of a Limit

In the following exercises (1-2), write the appropriate [latex]\varepsilon[/latex]–[latex]\delta[/latex] definition for each of the given statements.

  1. [latex]\underset{t\to b}{\lim}g(t)=M[/latex]
  2. [latex]\underset{x\to a}{\lim}\phi(x)=A[/latex]

The following graph of the function [latex]f[/latex] satisfies [latex]\underset{x\to 2}{\lim}f(x)=2[/latex]. In the following exercise, determine a value of [latex]\delta >0[/latex] that satisfies the statement.

A function drawn in quadrant one for x > 0. It is an increasing concave up function, with points approximately (0,0), (1, .5), (2,2), and (3,4).

  1. If [latex]0<|x-2|<\delta[/latex], then [latex]|f(x)-2|<0.5[/latex].

The following graph of the function [latex]f[/latex] satisfies [latex]\underset{x\to 3}{\lim}f(x)=-1[/latex]. In the following exercise, determine a value of [latex]\delta >0[/latex] that satisfies the statement.

A graph of a decreasing linear function, with points (0,2), (1,1), (2,0), (3,-1), (4,-2), and so on for x >= 0.

  1. If [latex]0<|x-3|<\delta[/latex], then [latex]|f(x)+1|<2[/latex].

The following graph of the function [latex]f[/latex] satisfies [latex]\underset{x\to 3}{\lim}f(x)=2[/latex]. In the following exercise, for the given value of [latex]\varepsilon[/latex], find a value of [latex]\delta >0[/latex] such that the precise definition of limit holds true.

A graph of an increasing linear function intersecting the x axis at about (2.25, 0) and going through the points (3,2) and, approximately, (1,-5) and (4,5).

  1. [latex]\varepsilon =3[/latex]

In the following exercise, use a graphing calculator to find a number [latex]\delta[/latex] such that the statement holds true.

  1. [latex]|\sqrt{x-4}-2|<0.1[/latex], whenever [latex]|x-8|<\delta[/latex]

In the following exercises (7-8), use the precise definition of limit to prove the given limits.

  1. [latex]\underset{x\to 3}{\lim}\dfrac{x^2-9}{x-3}=6[/latex]
  2. [latex]\underset{x\to 0}{\lim}x^4=0[/latex]

In the following exercises (9-10), use the precise definition of limit to prove the given one-sided limits.

  1. [latex]\underset{x\to 5^-}{\lim}\sqrt{5-x}=0[/latex]
  2. [latex]\underset{x\to 1^-}{\lim}f(x)=3[/latex], where [latex]f(x)=\begin{cases} 5x-2 & \text{ if } \, x < 1 \\ 7x-1 & \text{ if } x \ge 1 \end{cases}[/latex]

In the following exercise, use the precise definition of limit to prove the given infinite limit.

  1. [latex]\underset{x\to -1}{\lim}\dfrac{3}{(x+1)^2}=\infty[/latex]

For the following exercises (12-13), suppose that [latex]\underset{x\to a}{\lim}f(x)=L[/latex] and [latex]\underset{x\to a}{\lim}g(x)=M[/latex] both exist. Use the precise definition of limits to prove the following limit laws:

  1. [latex]\underset{x\to a}{\lim}(f(x)-g(x))=L-M[/latex]
  2. [latex]\underset{x\to a}{\lim}[f(x)g(x)]=LM[/latex].