Inverse Functions: Learn It 3

Lumen Learning

Inverse Functions: Learn It 3

Graphing Inverse Functions

Let’s consider the relationship between the graph of a function $f$ and the graph of its inverse.

Consider the graph of $f$ shown in Figure 9(a) and a point $(a,b)$ on the graph.

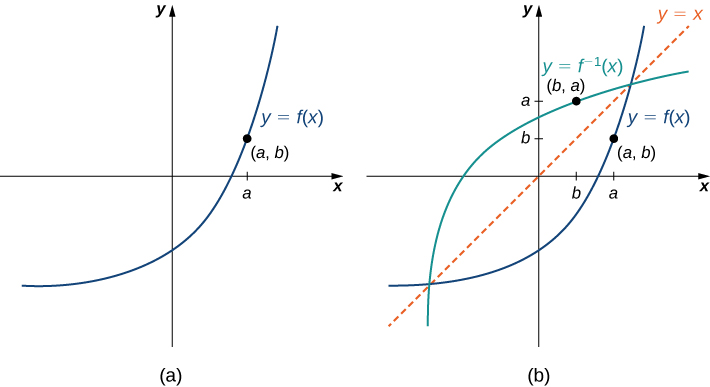
An image of two graphs. The first graph is of “y = f(x)”, which is a curved increasing function, that increases at a faster rate as x increases. The point (a, b) is on the graph of the function in the first quadrant. The second graph also graphs “y = f(x)” with the point (a, b), but also graphs the function “y = f inverse (x)”, an increasing curved function, that increases at a slower rate as x increases. This function includes the point (b, a). In addition to the two functions, there is a diagonal dotted line potted with the equation “y =x”, which shows that “f(x)” and “f inverse (x)” are mirror images about the line “y =x”. — Figure 9. (a) The graph of this function $f$ shows point $(a,b)$ on the graph of $f$ . (b) Since $(a,b)$ is on the graph of $f$ , the point $(b,a)$ is on the graph of $f^{-1}$ . The graph of $f^{-1}$ is a reflection of the graph of $f$ about the line $y=x$ .

Since $b=f(a)$ , then $f^{-1}(b)=a$ . Therefore, when we graph $f^{-1}$ , the point $(b,a)$ is on the graph. As a result, the graph of $f^{-1}$ is a reflection of the graph of $f$ about the line $y=x$ .

How to: Graph the Inverse of a Function

Plot the Function: Graph the original function $f(x)$ and plot a few key points.
Reflect Over Line: Reflect these points over the line $y=x$ to find the corresponding points on $f^{-1}$ .
Draw the Inverse: Connect these reflected points to graph the inverse function.
Check: Ensure that each point $(a,b)$ on the original function corresponds to the point $(b,a)$ on the inverse function.
Line of Symmetry: The line $y=x$ should act as a line of symmetry between the function and its inverse.

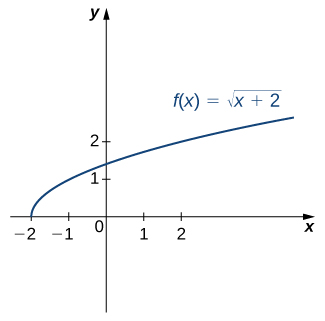
For the graph of $f$ in the following image, sketch a graph of $f^{-1}$ by sketching the line $y=x$ and using symmetry. Identify the domain and range of $f^{-1}$ .

An image of a graph. The x axis runs from -2 to 2 and the y axis runs from 0 to 2. The graph is of the function “f(x) = square root of (x +2)”, an increasing curved function. The function starts at the point (-2, 0). The x intercept is at (-2, 0) and the y intercept is at the approximate point (0, 1.4). — Figure 10. Graph of $f(x)$ .

Reflect the graph about the line $y=x$ . The domain of $f^{-1}$ is $[0,\infty)$ . The range of $f^{-1}$ is $[-2,\infty)$ . By using the preceding strategy for finding inverse functions, we can verify that the inverse function is $f^{-1}(x)=x^2-2$ , as shown in the graph.

An image of a graph. The x axis runs from -2 to 2 and the y axis runs from -2 to 2. The graph is of two functions. The first function is “f(x) = square root of (x +2)”, an increasing curved function. The function starts at the point (-2, 0). The x intercept is at (-2, 0) and the y intercept is at the approximate point (0, 1.4). The second function is “f inverse (x) = (x squared) -2”, an increasing curved function that starts at the point (0, -2). The x intercept is at the approximate point (1.4, 0) and the y intercept is at the point (0, -2). In addition to the two functions, there is a diagonal dotted line potted with the equation “y =x”, which shows that “f(x)” and “f inverse (x)” are mirror images about the line “y =x”. — Figure 11. Graph of $f(x)$ and its inverse.

Restricting Domains

As we have seen, $f(x)=x^2$ does not have an inverse function because it is not one-to-one. However, we can choose a subset of the domain of $f$ such that the function is one-to-one. This subset is called a restricted domain.

By restricting the domain of $f$ , we can define a new function $g$ such that the domain of $g$ is the restricted domain of $f$ and $g(x)=f(x)$ for all $x$ in the domain of $g$ . Then we can define an inverse function for $g$ on that domain.

For example, since $f(x)=x^2$ is one-to-one on the interval $[0,\infty)$ , we can define a new function $g$ such that the domain of $g$ is $[0,\infty)$ and $g(x)=x^2$ for all $x$ in its domain. Since $g$ is a one-to-one function, it has an inverse function, given by the formula $g^{-1}(x)=\sqrt{x}$ .

On the other hand, the function $f(x)=x^2$ is also one-to-one on the domain $(−\infty,0]$ . Therefore, we could also define a new function $h$ such that the domain of $h$ is $(−\infty,0]$ and $h(x)=x^2$ for all $x$ in the domain of $h$ . Then $h$ is a one-to-one function and must also have an inverse. Its inverse is given by the formula $h^{-1}(x)=−\sqrt{x}$ (Figure 13).

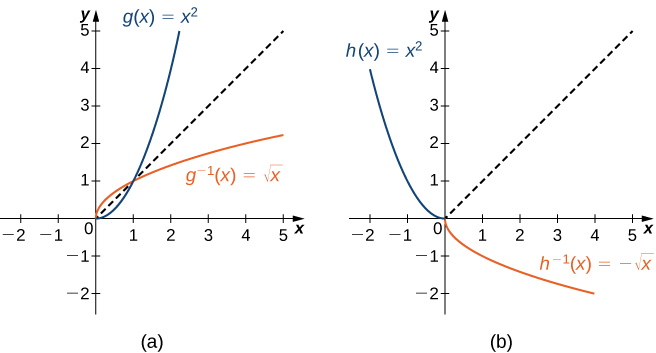
An image of two graphs. Both graphs have an x axis that runs from -2 to 5 and a y axis that runs from -2 to 5. The first graph is of two functions. The first function is “g(x) = x squared”, an increasing curved function that starts at the point (0, 0). This function increases at a faster rate for larger values of x. The second function is “g inverse (x) = square root of x”, an increasing curved function that starts at the point (0, 0). This function increases at a slower rate for larger values of x. The first function is “h(x) = x squared”, a decreasing curved function that ends at the point (0, 0). This function decreases at a slower rate for larger values of x. The second function is “h inverse (x) = -(square root of x)”, an increasing curved function that starts at the point (0, 0). This function decreases at a slower rate for larger values of x. In addition to the two functions, there is a diagonal dotted line potted with the equation “y =x”, which shows that “f(x)” and “f inverse (x)” are mirror images about the line “y =x”. — Figure 13. (a) For $g(x)=x^2$ restricted to $[0,\infty), \, g^{-1}(x)=\sqrt{x}$ . (b) For $h(x)=x^2$ restricted to $(−\infty,0], \, h^{-1}(x)=−\sqrt{x}$ .

restricted domain

Some functions don’t have inverses over their full domains because they’re not one-to-one. By restricting the domain, we ensure the function is one-to-one. Once the domain is restricted, we can define an inverse.

Consider the function $f(x)=(x+1)^2$ .

Sketch the graph of $f$ and use the horizontal line test to show that $f$ is not one-to-one.
Show that $f$ is one-to-one on the restricted domain $[-1,\infty)$ . Determine the domain and range for the inverse of $f$ on this restricted domain and find a formula for $f^{-1}$ .

The graph of $f$ is the graph of $y=x^2$ shifted left 1 unit. Since there exists a horizontal line intersecting the graph more than once, $f$ is not one-to-one.

Figure 14. Graph of the function $f(x)=(x+1)^2$ .
On the interval $[-1,\infty), \, f$ is one-to-one.

Figure 15. Looking at a restricted domain graph of a function.

The domain and range of $f^{-1}$ are given by the range and domain of $f$ , respectively. Therefore, the domain of $f^{-1}$ is $[0,\infty)$ and the range of $f^{-1}$ is $[-1,\infty)$ .

To find a formula for $f^{-1}$ , solve the equation $y=(x+1)^2$ for $x$ . If $y=(x+1)^2$ , then $x=-1 \pm \sqrt{y}$ . Since we are restricting the domain to the interval where $x \ge -1$ , we need $\pm \sqrt{y} \ge 0$ . Therefore, $x=-1+\sqrt{y}$ . Interchanging $x$ and $y$ , we write $y=-1+\sqrt{x}$ and conclude that $f^{-1}(x)=-1+\sqrt{x}$ .

Watch the following video to see the worked solution to this example.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this video using this link (opens in new window).