Inverse Functions: Learn It 1

  • Check if a function can have an inverse by using the horizontal line test
  • Determine a function’s inverse and draw its mirrored graph
  • Calculate values using inverse trig functions like arcsine, arccosine, and arctangent

Inverse Functions

An inverse function reverses the operation done by a particular function. In other words, whatever a function does, the inverse function undoes it. If we have a function [latex]f[/latex] that takes an input [latex]x[/latex] and produces an output [latex]f(x)[/latex], the inverse function, denoted as [latex]f^{−1}[/latex], takes [latex]f(x)[/latex] as its input and returns the original [latex]x[/latex] as its output. 

inverse functions

An inverse function reverses the effect of the original function, effectively ‘undoing’ what the original function does.

The inverse of a function [latex]f[/latex] is denoted by [latex]f^{−1}[/latex].

Note that [latex]f^{-1}[/latex] is read as “f inverse.” Here, the [latex]-1[/latex] is not used as an exponent and [latex]f^{-1}(x) \ne \frac{1}{f(x)}[/latex].

For instance, let’s consider the function [latex]f(x)=x^3+4[/latex]. To find the inverse, we set [latex]y= f(x)[/latex], which gives us [latex]y=x^3+4[/latex]. We get the inverse function [latex]f^{−1}(y)[/latex] by solving for [latex]x[/latex].

In this instance, subtract [latex]4[/latex] from both sides to get [latex]t-4=x^3[/latex], and then take the cube root of both sides. This gives us [latex]x=\sqrt[3]{y-4}[/latex].  This equation defines [latex]x[/latex] as a function of [latex]y[/latex].

Denoting this function as [latex]f^{-1}[/latex], and writing [latex]x=f^{-1}(y)=\sqrt[3]{y-4}[/latex], we see that for any [latex]x[/latex] in the domain of [latex]f, \, f^{-1}(f(x))=f^{-1}(x^3+4)=x[/latex].

Thus, this new function, [latex]f^{-1}[/latex], “undid” what the original function [latex]f[/latex] did. 

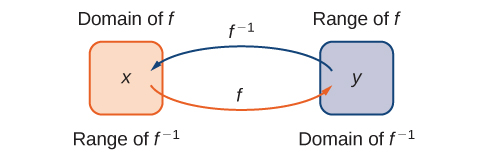
Two functions are inverses of each other if the domain [latex]D[/latex] of [latex]f[/latex] becomes the range [latex]R[/latex] of [latex]f^{−1}[/latex] and vice versa.

In other words, for a function [latex]f[/latex] and its inverse [latex]f^{-1}[/latex],

[latex]f^{-1}(f(x))=x[/latex] for all [latex]x[/latex] in [latex]D[/latex], and [latex]f(f^{-1}(y))=y[/latex] for all [latex]y[/latex] in [latex]R[/latex]

Figure 1 shows the relationship between the domain and range of [latex]f[/latex] and the domain and range of [latex]f^{-1}[/latex].

An image of two bubbles. The first bubble is orange and has two labels: the top label is “Domain of f” and the bottom label is “Range of f inverse”. Within this bubble is the variable “x”. An orange arrow with the label “f” points from this bubble to the second bubble. The second bubble is blue and has two labels: the top label is “range of f” and the bottom label is “domain of f inverse”. Within this bubble is the variable “y”. A blue arrow with the label “f inverse” points from this bubble to the first bubble.
Figure 1. Given a function [latex]f[/latex] and its inverse [latex]f^{-1}, \, f^{-1}(y)=x[/latex] if and only if [latex]f(x)=y[/latex]. The range of [latex]f[/latex] becomes the domain of [latex]f^{-1}[/latex] and the domain of [latex]f[/latex] becomes the range of [latex]f^{-1}[/latex].

Horizontal Line Test

Not all functions have inverses that are also functions, because for a function to have an inverse, each output must be linked to one and only one input. This unique pairing ensures that the inverse process can always match an output back to one specific input, fulfilling the definition of a function.

For example, let’s try to find the inverse function for [latex]f(x)=x^2[/latex]. Solving the equation [latex]y=x^2[/latex] for [latex]x[/latex], we arrive at the equation [latex]x= \pm \sqrt{y}[/latex]. This equation does not describe [latex]x[/latex] as a function of [latex]y[/latex] because there are two solutions to this equation for every [latex]y>0[/latex].

The problem with trying to find an inverse function for [latex]f(x)=x^2[/latex] is that two inputs are sent to the same output for each output [latex]y>0[/latex]. The function [latex]f(x)=x^3+4[/latex] discussed earlier did not have this problem. For that function, each input was sent to a different output.

A function that sends each input to a different output is called a one-to-one function.

one-to-one

A one-to-one function is a type of function in which each output value is paired with a unique input value. 

One way to determine whether a function is one-to-one is by looking at its graph. If a function is one-to-one, then no two inputs can be sent to the same output. Therefore, if we draw a horizontal line anywhere in the [latex]xy[/latex]-plane, it cannot intersect the graph more than once. This is known as the horizontal line test. 

Horizontal Line Test

A function [latex]f[/latex] is one-to-one, if and only if, every horizontal line intersects the graph of [latex]f[/latex] no more than once.

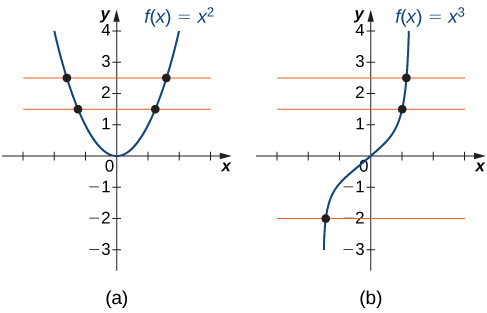
An image of two graphs. Both graphs have an x axis that runs from -3 to 3 and a y axis that runs from -3 to 4. The first graph is of the function “f(x) = x squared”, which is a parabola. The function decreases until it hits the origin, where it begins to increase. The x intercept and y intercept are both at the origin. There are two orange horizontal lines also plotted on the graph, both of which run through the function at two points each. The second graph is of the function “f(x) = x cubed”, which is an increasing curved function. The x intercept and y intercept are both at the origin. There are three orange lines also plotted on the graph, each of which only intersects the function at one point.
Figure 3. (a) The function [latex]f(x)=x^2[/latex] is not one-to-one because it fails the horizontal line test. (b) The function [latex]f(x)=x^3[/latex] is one-to-one because it passes the horizontal line test.

Note that the horizontal line test is different from the vertical line test. The vertical line test determines whether a graph is the graph of a function. The horizontal line test determines whether a function is one-to-one (Figure 3).

The Vertical Line Test

The vertical line test confirms whether a relation is a function by checking that every vertical line crosses the graph at most once. 

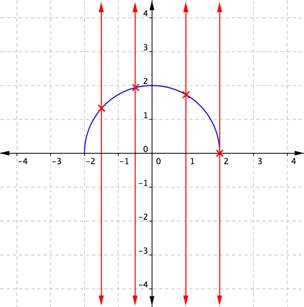
A graph of a semicircle. Four vertical lines cross the semicircle at one point each.
Figure 2. Semicircle graph undergoing the vertical line test.

When a vertical line is placed across the plot of this relation, it does not intersect the graph more than once for any values of [latex]x[/latex]. This is a graph of a function.

If, on the other hand, a graph shows two or more intersections with a vertical line, then an input ([latex]x[/latex]-coordinate) can have more than one output ([latex]y[/latex]-coordinate), and [latex]y[/latex] is not a function of [latex]x[/latex]. 

For each of the following functions, use the horizontal line test to determine whether it is one-to-one.

a.

An image of a graph. The x axis runs from -3 to 11 and the y axis runs from -3 to 11. The graph is of a step function which contains 10 horizontal steps. Each steps starts with a closed circle and ends with an open circle. The first step starts at the origin and ends at the point (1, 0). The second step starts at the point (1, 1) and ends at the point (1, 2). Each of the following 8 steps starts 1 unit higher in the y direction than where the previous step ended. The tenth and final step starts at the point (9, 9) and ends at the point (10, 9)
Figure 4.

b.

An image of a graph. The x axis runs from -3 to 6 and the y axis runs from -3 to 6. The graph is of the function “f(x) = (1/x)”, a curved decreasing function. The graph of the function starts right below the x axis in the 4th quadrant and begins to decreases until it comes close to the y axis. The graph keeps decreasing as it gets closer and closer to the y axis, but never touches it due to the vertical asymptote. In the first quadrant, the graph of the function starts close to the y axis and keeps decreasing until it gets close to the x axis. As the function continues to decreases it gets closer and closer to the x axis without touching it, where there is a horizontal asymptote.
Figure 5.