Inverse Functions: Fresh Take

Lumen Learning

Inverse Functions: Fresh Take

Identify conditions for a function’s inverse using the horizontal line test
Find the inverse of a function and graph its reflection
Evaluate inverse trigonometric functions

Inverse Functions

The Main Idea

Definition of Inverse Functions:
- An inverse function “undoes” what the original function does
- Notation: $f^{-1}$ is the inverse of $f$
- $f^{-1}(f(x)) = x$ and $f(f^{-1}(x)) = x$
Domain and Range Relationship:
- Domain of $f$ becomes the range of $f^{-1}$
- Range of $f$ becomes the domain of $f^{-1}$
One-to-One Functions:
- Each element in the codomain is paired with at most one element in the domain
- Only one-to-one functions have inverses that are also functions
Horizontal Line Test:
- Determines if a function is one-to-one
- A function passes if no horizontal line intersects its graph more than once
Inverse Function Properties:
- Reverses the input and output of the original function
- Graphically, it’s a reflection of the original function over $y = x$

Is the function $f$ graphed in the following image one-to-one?

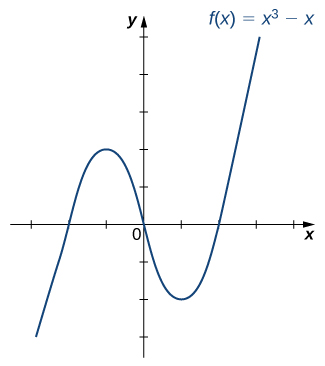
An image of a graph. The x axis runs from -3 to 4 and the y axis runs from -3 to 5. The graph is of the function “f(x) = (x cubed) - x” which is a curved function. The function increases, decreases, then increases again. The x intercepts are at the points (-1, 0), (0,0), and (1, 0). The y intercept is at the origin. — Figure 8. Is this function one-to-one?

Finding a Function’s Inverse

The Main Idea

The process for finding an inverse function is:

Ensure the function is one-to-one
Replace $f(x)$ with $y$
Solve the equation for $x$
Interchange $x$ and $y$
Replace $y$ with $f^{-1}(x)$

You can always check and verify if you have found a functions inverse by:

Checking that $f^{-1}(f(x)) = x$
Also verifying that $f(f^{-1}(x)) = x$

Find the inverse of the function $f(x)=\dfrac{3x}{(x-2)}$ . State the domain and range of the inverse function.

$f^{-1}(x)=\dfrac{2x}{x-3}$ .

The domain of $f^{-1}$ is $\{x|x \ne 3\}$ .

The range of $f^{-1}$ is $\{y|y \ne 2\}$ .

Find the inverse of $f(x) = (x + 2)³ - 1$ . State the domain and range of the inverse function.

f604f497-fe26-4bdf-be5f-a8a0d29c74d6

Ensure f(x) is one-to-one:
- $f(x)$ is a cubic function with no turning points, so it’s one-to-one.
Replace $f(x)$ with $y$ :
$y = (x + 2)³ - 1$
Solve for $x$ :
$\begin{align*}y + 1 &= (x + 2)³ \\ \sqrt[3]{(y + 1)} &= x + 2 \\ \sqrt[3]{(y + 1)} - 2 &= x\end{align*}$
Interchange $x$ and $y$ :
$y = \sqrt[3]{(x + 1)} - 2$
Replace $y$ with $f^{-1}(x)$ :
$f^{-1}(x) = \sqrt[3]{(x + 1)} - 2$
Verify:
$f(f^{-1}(x)) = ((\sqrt[3]{(x + 1)} - 2) + 2)³ - 1 = (\sqrt[3]{(x + 1)})³ - 1 = (x + 1) - 1 = x$
Domain and Range:
- Domain of $f$ : $(-∞, ∞)$ → Range of $f^{-1}$ : $(-∞, ∞)$
- Range of $f$ : $(-∞, ∞)$ → Domain of $f^{-1}$ : $(-∞, ∞)$

Graphing Inverse Functions

The Main Idea

Graphical Relationship of Inverses:
- Inverse functions are reflections of each other over the line $y = x$
- Points $(a,b)$ on $f(x)$ correspond to points $(b,a)$ on $f^{-1}(x)$
Graphing Inverse Functions:
- Plot the original function
- Reflect points over $y = x$
- Connect reflected points to form the inverse function’s graph
Restricted Domains:
- Used when a function is not one-to-one over its entire domain
- Allows creation of an inverse function for a portion of the original function
- Different restrictions can lead to different inverse functions
One-to-One on Restricted Domains:
- Ensure the function passes the horizontal line test on the restricted domain
- Domain of $f$ becomes range of $f^{-1}$ and vice versa

Sketch the graph of $f(x)=2x+3$ and the graph of its inverse using the symmetry property of inverse functions.

The graphs are symmetric about the line $y=x$ .

An image of a graph. The x axis runs from -3 to 4 and the y axis runs from -3 to 5. The graph is of two functions. The first function is “f(x) = 2x +3”, an increasing straight line function. The function has an x intercept at (-1.5, 0) and a y intercept at (0, 3). The second function is “f inverse (x) = (x - 3)/2”, an increasing straight line function, which increases at a slower rate than the first function. The function has an x intercept at (3, 0) and a y intercept at (0, -1.5). In addition to the two functions, there is a diagonal dotted line potted with the equation “y =x”, which shows that “f(x)” and “f inverse (x)” are mirror images about the line “y =x”. — Figure 12. Graph of $f(x)=2x+3$ and its inverse.

Consider $f(x)=\dfrac{1}{x^2}$ restricted to the domain $(−\infty ,0)$ . Verify that $f$ is one-to-one on this domain. Determine the domain and range of the inverse of $f$ and find a formula for $f^{-1}$ .

The domain and range of $f^{-1}$ is given by the range and domain of $f$ , respectively. To find $f^{-1}$ , solve $y=\dfrac{1}{x^2}$ for $x$ .

The domain of $f^{-1}$ is $(0,\infty)$ . The range of $f^{-1}$ is $(−\infty ,0)$ . The inverse function is given by the formula $f^{-1}(x)=\dfrac{-1 }{\sqrt{x}}$ .

Inverse Trigonometric Functions

The Main Idea

Definition of Inverse Trigonometric Functions:
- Created by restricting domains of standard trig functions
- Inverse sine ( $\sin^{-1}$ or arcsin), inverse cosine ( $\cos^{-1}$ or arccos), inverse tangent ( $\tan^{-1}$ or arctan), etc.
Domains and Ranges:
- arcsin and arccos: Domain $[-1, 1],$ Range $[\frac{-π}{2}, \frac{π}{2}]$ (arcsin) and $[0, π]$ (arccos)
- arctan: Domain $(-\infty, \infty)$ , Range $[\frac{-π}{2}, \frac{π}{2}]$
Graphs:
- Reflections of restricted trigonometric functions over $y = x$
Composition Properties:
- $\sin(\sin^{-1}(x)) = x$ for $x$ in $[-1, 1]$
- $\sin^{-1}(\sin(x)) = x$ for $x$ in $[\frac{-π}{2}, \frac{π}{2}]$
- Similar properties for other inverse trig functions

Evaluate and simplify the following:

$\cos^{-1}(-1/2)$
$\sin(\tan^{-1}(1))$
$\sin^{-1}(\sin(\frac{5π}{6}))$

Evaluating $\cos^{-1}(-\frac{1}{2})$ is equivalent to finding the angle $\theta$ such that $\cos\theta = -\frac{1}{2}$ and $0 \leq \theta \leq \pi$ .

The angle $\theta = \frac{2\pi}{3}$ satisfies these two conditions. Therefore, $\cos^{-1}(-\frac{1}{2}) = \frac{2\pi}{3}$ .
First we use the fact that $\tan^{-1}(1) = \frac{\pi}{4}$ . Then $\sin(\frac{\pi}{4}) = \frac{1}{\sqrt{2}}$ .

Therefore, $\sin(\tan^{-1}(1)) = \frac{1}{\sqrt{2}}$ .
To evaluate $\sin^{-1}(\sin(\frac{5\pi}{6}))$ , first use the fact that $\sin(\frac{5\pi}{6}) = \frac{1}{2}$ . Then we need to find the angle $\theta$ such that $\sin(\theta) = \frac{1}{2}$ and $-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}$ .

Since $\frac{\pi}{6}$ satisfies both these conditions, we have $\sin^{-1}(\sin(\frac{5\pi}{6})) = \sin^{-1}(\frac{1}{2}) = \frac{\pi}{6}$ .