Infinite Limits
Evaluating limits, whether at a specific point or as we approach it from a particular direction, helps us understand how functions behave near that point. While some functions have limits that are finite numbers, others grow without bound—these are cases of infinite limits.
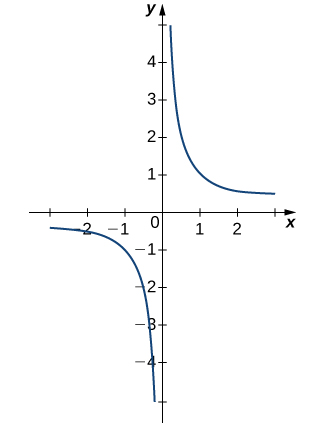
We now turn our attention to [latex]h(x)=\frac{1}{(x-2)^2}[/latex] (Figure 1 part c).
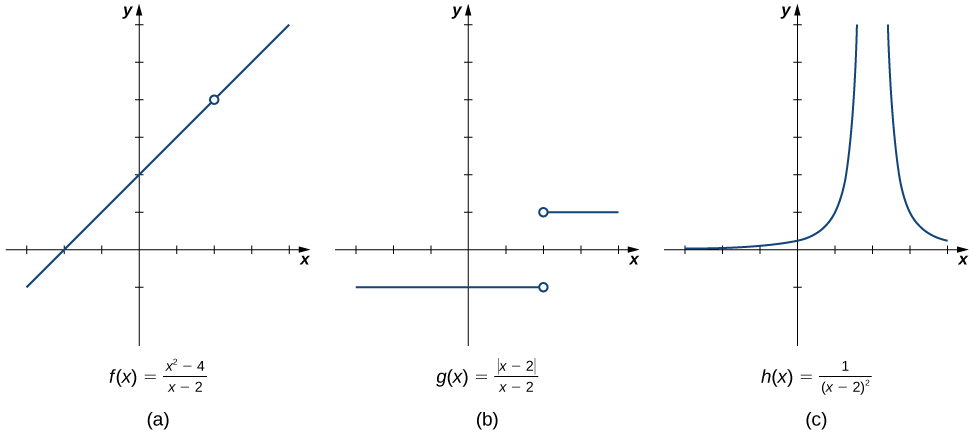
As [latex]x[/latex] gets closer to [latex]2[/latex], [latex]h(x)[/latex] increases without limit. This unbounded growth means that as [latex]x[/latex] approaches [latex]2[/latex], [latex]h(x)[/latex] heads towards positive infinity, which we denote as:
Infinite limits can be understood through the following general definitions.
infinite limits
Infinite limits from the left: For a function [latex]f(x)[/latex] within an interval that ends at [latex]a[/latex], we say:
- The limit is [latex]+∞[/latex] if [latex]f(x)[/latex] increases without bound as [latex]x[/latex] approaches [latex]a[/latex] from the left.
[latex]\underset{x\to a^-}{\lim}f(x)=+\infty[/latex].
- The limit is [latex]-∞[/latex] if [latex]f(x)[/latex] decreases without bound as [latex]x[/latex] approaches [latex]a[/latex] from the left.
[latex]\underset{x\to a^-}{\lim}f(x)=−\infty[/latex].
Infinite limits from the right: For a function [latex]f(x)[/latex] within an interval that ends at [latex]a[/latex], we say:
- The limit is [latex]+∞[/latex] if [latex]f(x)[/latex] increases without bound as [latex]x[/latex] approaches [latex]a[/latex] from the right.
[latex]\underset{x\to a^+}{\lim}f(x)=+\infty[/latex].
- The limit is [latex]-∞[/latex] if [latex]f(x)[/latex] decreases without bound as [latex]x[/latex] approaches [latex]a[/latex] from the right.
[latex]\underset{x\to a^+}{\lim}f(x)=−\infty[/latex].
Two-sided infinite limit: For a function [latex]f(x)[/latex] defined at all points except at [latex]a[/latex]:
- If [latex]f(x)[/latex] increases without bound from both sides as [latex]x[/latex] approaches [latex]a[/latex], the limit is [latex]+∞[/latex].
[latex]\underset{x\to a}{\lim}f(x)=+\infty[/latex].
- If [latex]f(x)[/latex] decreases without bound from both sides as [latex]x[/latex] approaches [latex]a[/latex], the limit is [latex]-∞[/latex].
[latex]\underset{x\to a}{\lim}f(x)=−\infty[/latex].
It is important to understand that when we write statements such as [latex]\underset{x\to a}{\lim}f(x)=+\infty[/latex] or [latex]\underset{x\to a}{\lim}f(x)=−\infty[/latex] we are describing the behavior of the function, as we have just defined it. We are not asserting that a limit exists.
For the limit of a function [latex]f(x)[/latex] to exist at [latex]a[/latex], it must approach a real number [latex]L[/latex] as [latex]x[/latex] approaches [latex]a[/latex]. That said, if, for example, [latex]\underset{x\to a}{\lim}f(x)=+\infty[/latex], we always write [latex]\underset{x\to a}{\lim}f(x)=+\infty[/latex] rather than [latex]\underset{x\to a}{\lim}f(x)[/latex] DNE.
Evaluate each of the following limits, if possible. Use a table of functional values and graph [latex]f(x)=\frac{1}{x}[/latex] to confirm your conclusion.
- [latex]\underset{x\to 0^-}{\lim}\frac{1}{x}[/latex]
- [latex]\underset{x\to 0^+}{\lim}\frac{1}{x}[/latex]
- [latex]\underset{x\to 0}{\lim}\frac{1}{x}[/latex]
Vertical Asymptotes
Continuing our exploration of infinite limits, it is worth highlighting functions like [latex]f(x)=\dfrac{1}{(x-a)^n}[/latex], where [latex]n[/latex] is a positive integer, to illustrate the concept further. Such functions exhibit notable behavior as [latex]x[/latex] approaches [latex]a[/latex]: they tend toward infinity. Whether approaching from the left or the right, these functions have no finite limit at [latex]a[/latex], and instead, they soar towards positive or negative infinity, depending on the parity of [latex]n[/latex]. This tendency is depicted in Figure 9.
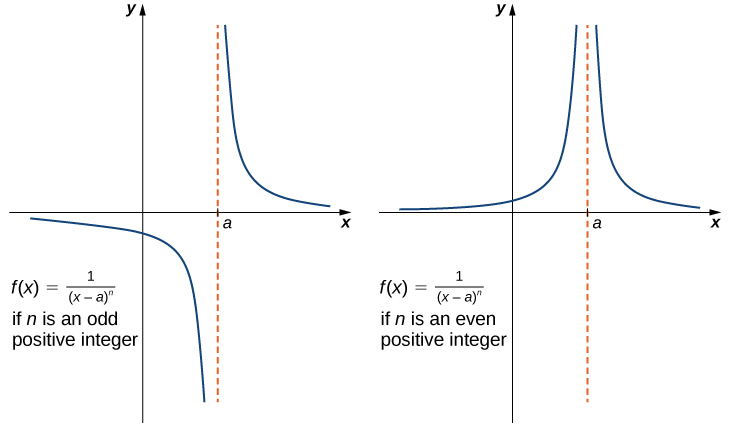
asymptotic behavior of power functions
If [latex]n[/latex] is a positive even integer, then
If [latex]n[/latex] is a positive odd integer, then
and
As we see in the graph, as [latex]x[/latex] approaches the value of [latex]a[/latex], regardless of the direction, the function values either increase or decrease sharply. This rapid change is visually represented by how the function’s curve approaches, but never touches, the vertical line [latex]x=a[/latex]. This specific line is known as a vertical asymptote, which is a boundary the function will never cross or reach.
vertical asymptote
A vertical asymptote is a line that a function approaches but never intersects or reaches as the inputs get infinitely close to a particular point.
Let [latex]f(x)[/latex] be a function. If any of the following conditions hold, then the line [latex]x=a[/latex] is a vertical asymptote of [latex]f(x)[/latex]:
Evaluate each of the following limits. Identify any vertical asymptotes of the function [latex]f(x)=\dfrac{1}{(x+3)^4}[/latex].
- [latex]\underset{x\to -3^-}{\lim}\dfrac{1}{(x+3)^4}[/latex]
- [latex]\underset{x\to -3^+}{\lim}\dfrac{1}{(x+3)^4}[/latex]
- [latex]\underset{x\to -3}{\lim}\dfrac{1}{(x+3)^4}[/latex]
In the next example, we put our knowledge of various types of limits to use to analyze the behavior of a function at several different points.
Use the graph of [latex]f(x)[/latex] in Figure 10 to determine each of the following values:
- [latex]\underset{x\to -4^-}{\lim}f(x); \, \underset{x\to -4^+}{\lim}f(x); \, \underset{x\to -4}{\lim}f(x); \, f(-4)[/latex]
- [latex]\underset{x\to -2^-}{\lim}f(x); \, \underset{x\to -2^+}{\lim}f(x); \, \underset{x\to -2}{\lim}f(x); \, f(-2)[/latex]
- [latex]\underset{x\to 1^-}{\lim}f(x); \, \underset{x\to 1^+}{\lim}f(x); \, \underset{x\to 1}{\lim}f(x); \, f(1)[/latex]
![The graph of a function f(x) described by the above limits and values. There is a smooth curve for values below x=-2; at (-2, 3), there is an open circle. There is a smooth curve between (-2, 1] with a closed circle at (1,6). There is an open circle at (1,3), and a smooth curve stretching from there down asymptotically to negative infinity along x=3. The function also curves asymptotically along x=3 on the other side, also stretching to negative infinity. The function then changes concavity in the first quadrant around y=4.5 and continues up.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11202918/CNX_Calc_Figure_02_02_015.jpg)
Figure 10. The graph shows [latex]f(x)[/latex].