Introduction to the Limit of a Function: Learn It 3

Lumen Learning

Introduction to the Limit of a Function: Learn It 3

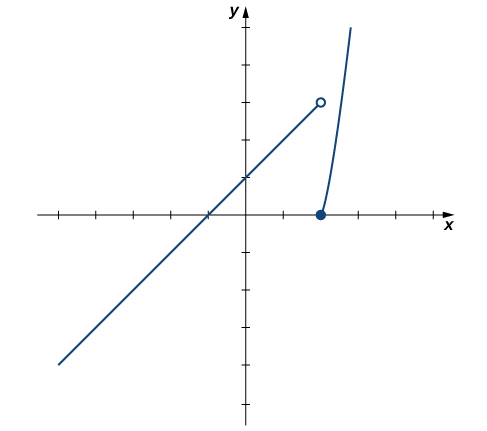
One-Sided Limits

Sometimes indicating that the limit of a function fails to exist at a point does not provide us with enough information about the behavior of the function at that particular point.

To see this, we now revisit the function $g(x)=\frac{|x-2|}{(x-2)}$ introduced at the beginning of the section (Figure 1 part b).

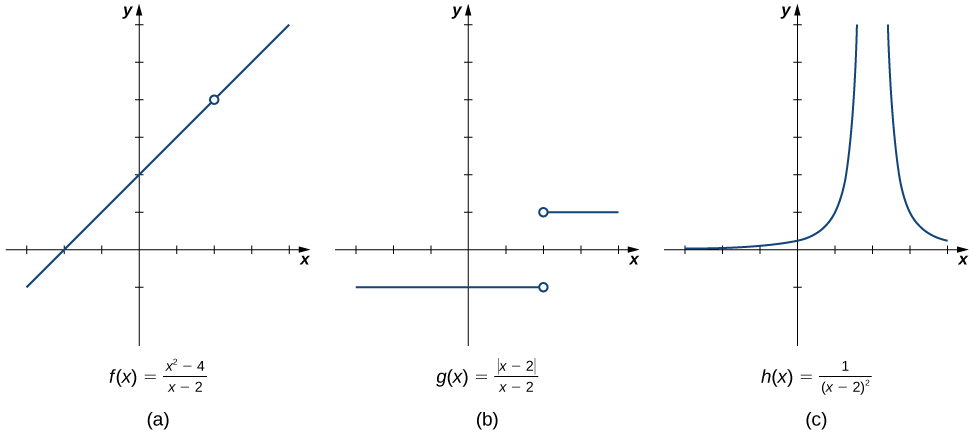
"Three 2 and x= -1 for x < 2. There are open circles at both endpoints (2, 1) and (-2, 1). The third is h(x) = 1 / (x-2)^2, in which the function curves asymptotically towards y=0 and x=2 in quadrants one and two." width="975" height="434" — Figure 1. These graphs show the behavior of three different functions around $x=2$ .

As we pick values of $x$ close to $2$ , $g(x)$ does not approach a single value, so the limit as $x$ approaches $2$ does not exist—that is, $\underset{x\to 2}{\lim}g(x)$ DNE.

However, this statement alone does not give us a complete picture of the behavior of the function around the $x$ -value $2$ . To provide a more accurate description, we introduce the idea of a one-sided limit.

For all values to the left of $2$ (or the negative side of $2$ ), $g(x)=-1$ . Thus, as $x$ approaches $2$ from the left, $g(x)$ approaches $−1$ .

Mathematically, we say that the limit as $x$ approaches $2$ from the left is $−1$ . Symbolically, we express this idea as

lim_{x \to 2^{-}} g (x) = - 1

$\underset{x\to 2^-}{\lim}g(x)=-1$

Similarly, as $x$ approaches $2$ from the right (or from the positive side), $g(x)$ approaches $1$ . Symbolically, we express this idea as

lim_{x \to 2^{+}} g (x) = 1

$\underset{x\to 2^+}{\lim}g(x)=1$

one-sided limits

One-sided limits are limits approached from one direction—either from the left or the right.

Left-Sided Limit: For a function $f(x)$ on an interval ending at $a$ , if $f(x)$ approaches a specific value $L$ as the values of $x$ approaches $a$ from the left ( $x < a$ ), we denote this limit as:
$\underset{x\to a^-}{\lim}f(x)=L$
Right-Sided Limit: For a function $f(x)$ on an interval ending at $a$ , if $f(x)$ approaches a specific value $L$ as the values of $x$ approaches $a$ from the right ( $x > a$ ), we express this limit as:
$\underset{x\to a^+}{\lim}f(x)=L$

For the function $f(x)=\begin{cases} x+1, & \text{ if } \, x < 2 \\ x^2-4, & \text{ if } \, x \ge 2 \end{cases}$ , evaluate each of the following limits.

$\underset{x\to 2^-}{\lim}f(x)$
$\underset{x\to 2^+}{\lim}f(x)$

We can use tables of functional values again. Observe that for values of $x$ less than $2$ , we use $f(x)=x+1$ and for values of $x$ greater than $2$ , we use $f(x)=x^2-4$ .

Table of Functional Values for $f(x)=\begin{cases} x+1, & \text{ if } \, x < 2 \\ x^2-4, & \text{ if } \, x \ge 2 \end{cases}$
$x$	$f(x)=x+1$	$x$	$f(x)=x^2-4$
$1.9$	$2.9$	$2.1$	$0.41$
$1.99$	$2.99$	$2.01$	$0.0401$
$1.999$	$2.999$	$2.001$	$0.004001$
$1.9999$	$2.9999$	$2.0001$	$0.00040001$
$1.99999$	$2.99999$	$2.00001$	$0.0000400001$

Based on this table, we can conclude that

$\underset{x\to 2^-}{\lim}f(x)=3$
$\underset{x\to 2^+}{\lim}f(x)=0$ .

Therefore, the (two-sided) limit of $f(x)$ does not exist at $x=2$ . Figure 7 shows a graph of $f(x)$ and reinforces our conclusion about these limits.

"The

Watch the following video to see the worked solution to this example.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this video using this link (opens in new window).

Two-Sided Limits

To fully grasp how limits function, it’s essential to understand the connection between one-sided and two-sided limits.

A two-sided limit at a point exists only if the one-sided limits from both the left and the right converge to the same value. If there’s a discrepancy between the left and the right limits, the two-sided limit at that point does not exist.

two-sided limits

For a function $f(x)$ , defined over an interval including $a$ (except possibly at $a$ itself), we say the two-sided limit exists as $x$ approaches $a$ and equals $L$ if, and only if, both one-sided limits as $x$ approaches $a$ also equals $L$ .

lim_{x \to a} f (x) = L

$\underset{x\to a}{\lim}f(x)=L$ , if and only if

lim_{x \to a^{-}} f (x) = L

$\underset{x\to a^-}{\lim}f(x)=L$ and

lim_{x \to a^{+}} f (x) = L

$\underset{x\to a^+}{\lim}f(x)=L$