Introduction to the Limit of a Function: Learn It 1

Lumen Learning

Introduction to the Limit of a Function: Learn It 1

Understand how to write the limit of a function using the correct symbols and estimate limits by examining tables and graphs
Understand one-sided limits (approaching a point from only one direction) and how they relate to two-sided limits
Understand and use the proper notation for infinite limits and define vertical asymptotes

The Definition of a Limit

We begin our exploration of limits by taking a look at the graphs of the functions

f (x) = \frac{x^{2} - 4}{x - 2}, g (x) = \frac{| x - 2 |}{x - 2}

$f(x)=\dfrac{x^2-4}{x-2}, \ \, g(x)=\dfrac{|x-2|}{x-2}$ , and

h (x) = \frac{1}{(x - 2)^{2}}

$h(x)=\dfrac{1}{(x-2)^2}$ ,

which are shown in Figure 1. In particular, let’s focus our attention on the behavior of each graph at and around $x=2$ .

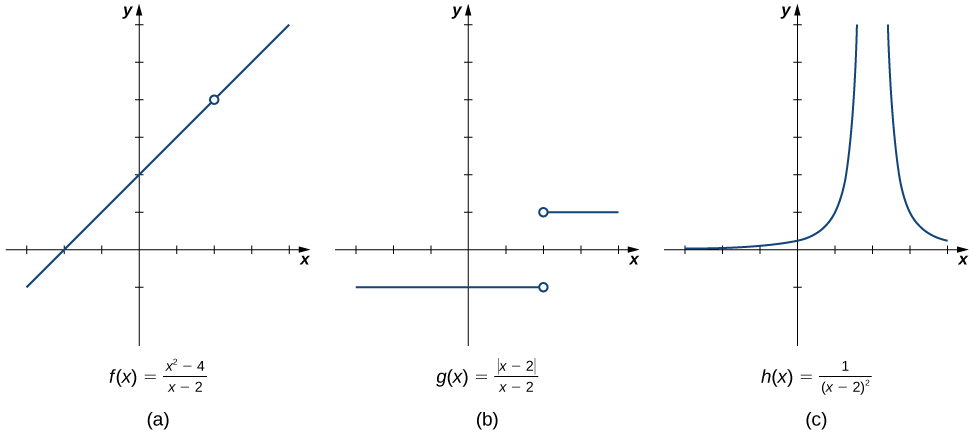
"Three 2 and x= -1 for x < 2. There are open circles at both endpoints (2, 1) and (-2, 1). The third is h(x) = 1 / (x-2)^2, in which the function curves asymptotically towards y=0 and x=2 in quadrants one and two." width="975" height="434" — Figure 1. These graphs show the behavior of three different functions around $x=2$ .

Each of the three functions is undefined at $x=2$ , but if we make this statement and no other, we give a very incomplete picture of how each function behaves in the vicinity of $x=2$ . To express the behavior of each graph in the vicinity of $2$ more completely, we need to introduce the concept of a limit.

Intuitive Definition of a Limit

Let’s examine how the function $f(x)=\dfrac{(x^2-4)}{(x-2)}$ behaves as f $x$ approachs $2$ . While $f(x)$ isn’t defined at $x=2$ , as $x$ gets closer to $2$ from either side, $f(x)$ approaches $4$ .

Mathematically, we say that the limit of $f(x)$ as $x$ approaches $2$ is $4$ . We express this observation using limit notation as:

lim_{x \to 2} f (x) = 4

$\underset{x \to 2}{\lim}f(x)=4$

This initial exploration into limits leads us to a more formal definition.

Consider the limit of a function at a specific point as the value that the function’s output gets closer to, as the input values approach that point. Assuming such a value exists, we can articulate this concept more precisely with the following definition:

limit definition

For a function $f(x)$ defined over an open interval around a point $a$ , possibly excluding $a$ itself, if all function values $f(x)$ get arbitrarily close to some real number $L$ as $x$ approaches $a$ , then $L$ is the limit of $f(x)$ as $x$ approaches $a$ .

Limit Notation: lim_{x \to a} f (x) = L

$\text{Limit Notation: } \underset{x\to a}{\lim}f(x)=L$

A more succinct way to understand this definition: As $x$ gets closer to $a$ , $f(x)$ gets closer and stays close to $L$ .

Estimating Limits Using Tables

We can estimate limits by constructing tables of functional values.

How to: Evaluate a Limit Using a Table of Functional Values

To find

lim_{x \to a} f (x)

$\underset{x\to a}{\lim}f(x)$ , create a table with two sets of

x

$x$ -values: those just less than

a

$a$ and those just more than

a

$a$ . The table below demonstrates what your tables might look like.

Table of Functional Values for $\underset{x\to a}{\lim}f(x)$
$x$	$f(x)$	$x$	$f(x)$
$a-0.1$	$f(a-0.1)$	$a+0.1$	$f(a+0.1)$
$a-0.01$	$f(a-0.01)$	$a+0.01$	$f(a+0.01)$
$a-0.001$	$f(a-0.001)$	$a+0.001$	$f(a+0.001)$
$a-0.0001$	$f(a-0.0001)$	$a+0.0001$	$f(a+0.0001)$
Use additional values as necessary.		Use additional values as necessary.

Analyze the $f(x)$ values. If they get closer to a single number as $x$ approaches $a$ from both sides, that’s the limit.
If both sides of $f(x)$ is confirmed. If not, the limit may not exist.
Use the graph of $f(x)$ to verify your results. By plotting the function and zooming in around $x=a$ , you can observe if $f(x)$ approaches the limit you calculated. This visual check complements the numerical approach.

Evaluate $\underset{x\to 4}{\lim}\dfrac{\sqrt{x}-2}{x-4}$ using a table of functional values.

As before, we use a table to list the values of the function for the given values of $x$ .

Table of Functional Values for $\underset{x\to 4}{\lim}\frac{\sqrt{x}-2}{x-4}$
$x$	$\frac{\sqrt{x}-2}{x-4}$	$x$	$\frac{\sqrt{x}-2}{x-4}$
$3.9$	$0.251582341869$	$4.1$	$0.248456731317$
$3.99$	$0.25015644562$	$4.01$	$0.24984394501$
$3.999$	$0.250015627$	$4.001$	$0.249984377$
$3.9999$	$0.250001563$	$4.0001$	$0.249998438$
$3.99999$	$0.25000016$	$4.00001$	$0.24999984$

After inspecting this table, we see that the functional values less than $4$ appear to be decreasing toward $0.25$ whereas the functional values greater than $4$ appear to be increasing toward $0.25$ . We conclude that $\underset{x\to 4}{\lim}\frac{\sqrt{x}-2}{x-4}=0.25$ . We confirm this estimate using the graph of $f(x)=\frac{\sqrt{x}-2}{x-4}$ shown in Figure 3.

A graph of the function f(x) = (sqrt(x) – 2 ) / (x-4) over the interval [0,8]. There is an open circle on the function at x=4. The function curves asymptotically towards the x axis and y axis in quadrant one. — Figure 3. The graph of $f(x)=\frac{\sqrt{x}-2}{x-4}$ confirms the estimate from the table.