Introduction to the Limit of a Function: Fresh Take

Lumen Learning

Introduction to the Limit of a Function: Fresh Take

Define the limit of a function using proper notation and estimate limits from tables and graphs
Define one-sided limits with examples and explain their relationship to two-sided limits.
Describe infinite limits using correct notation and define vertical asymptotes

The Definition of a Limit

The Main Idea

Intuitive Definition of a Limit:
- As $x$ approaches $a$ , $f(x)$ gets arbitrarily close to $L$
- Notation: $\lim_{x \to a} f(x) = L$
Estimating Limits: a. Using Tables:
- Create tables approaching the point from both sides
- Observe if values converge to a single number b. Using Graphs:
- Examine function behavior near the point of interest
- Look for y-value that the function approaches
Basic Limit Properties:
- $\lim_{x \to a} x = a$
- $\lim_{x \to a} c = c$ (c is a constant)
Existence of Limits:
- A limit exists if function values converge to a single, real number
- Limits may not exist due to oscillation or divergence

Evaluate $\underset{x\to 0}{\lim}\dfrac{\sin x}{x}$ using a table of functional values.

We have calculated the values of

$f(x)=\dfrac{(\sin x)}{x}$ for the values of

$x$ listed in the table below.

Table of Functional Values for $\underset{x\to 0}{\lim}\frac{\sin x}{x}$
$x$	$\frac{\sin x}{x}$	$x$	$\frac{\sin x}{x}$
−0.1	0.998334166468	0.1	0.998334166468
−0.01	0.999983333417	0.01	0.999983333417
−0.001	0.999999833333	0.001	0.999999833333
−0.0001	0.999999998333	0.0001	0.999999998333

Note: The values in this table were obtained using a calculator and using all the places given in the calculator output.

As we read down each $\frac{\sin x}{x}$ column, we see that the values in each column appear to be approaching one. Thus, it is fairly reasonable to conclude that $\underset{x\to 0}{\lim}\frac{\sin x}{x}=1$ . A calculator-or computer-generated graph of $f(x)=\frac{\sin x}{x}$ would be similar to that shown in Figure 2, and it confirms our estimate.

A graph of f(x) = sin(x)/x over the interval [-6, 6]. The curving function has a y intercept at x=0 and x intercepts at y=pi and y=-pi. — Figure 2. The graph of $f(x)=(\sin x)/x$ confirms the estimate from the table.

Estimate $\underset{x\to 1}{\lim}\dfrac{\frac{1}{x}-1}{x-1}$ using a table of functional values. Use a graph to confirm your estimate.

Use $0.9, 0.99, 0.999, 0.9999, 0.99999$ and $1.1, 1.01, 1.001, 1.0001, 1.00001$ as your table values.

$\underset{x\to 1}{\lim}\frac{\frac{1}{x}-1}{x-1}=-1$

Use the graph of $h(x)$ in the figure below to evaluate $\underset{x\to 2}{\lim}h(x)$ , if possible.

A graph of the function h(x), which is a parabola graphed over [-2.5, 5]. There is an open circle where the vertex should be at the point (2,-1). — Figure 5. The graph of $h(x)$ consists of a smooth graph with a single removed point at $x=2$ .

What $y$ -value does the function approach as the $x$ -values approach $2$ ?

$\underset{x\to 2}{\lim}h(x)=-1$ .

Use a table of functional values to evaluate $\underset{x\to 2}{\lim}\dfrac{|x^2-4|}{x-2}$ , if possible.

Use $x$ -values $1.9, 1.99, 1.999, 1.9999, 1.9999$ and $2.1, 2.01, 2.001, 2.0001, 2.00001$ in your table.

$\underset{x\to 2}{\lim}\frac{|x^2-4|}{x-2}$ does not exist.

One-Sided and Two-Sided Limits

The Main Idea

One-Sided Limits:
- Left-hand limit: $\lim_{x \to a^-} f(x) = L$
- Right-hand limit: $\lim_{x \to a^+} f(x) = L$
Two-Sided Limits:
- Exist only if both one-sided limits exist and are equal
- $\lim_{x \to a} f(x) = L$ if and only if $\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) = L$
Relationship between One-Sided and Two-Sided Limits:
- Two-sided limit exists if and only if both one-sided limits exist and are equal
- If one-sided limits differ, the two-sided limit does not exist
Evaluating One-Sided Limits:
- Use tables of values approaching from left or right
- Examine graphs for behavior as $x$ approaches $a$ from each side

Use a table of functional values to estimate the following limits, if possible.

$\underset{x\to 2^-}{\lim}\dfrac{|x^2-4|}{x-2}$
$\underset{x\to 2^+}{\lim}\dfrac{|x^2-4|}{x-2}$

Use $x$ -values $1.9, 1.99, 1.999, 1.9999, 1.9999$ to estimate $\underset{x\to 2^-}{\lim}\frac{|x^2-4|}{x-2}$ .
Use $x$ -values $2.1, 2.01, 2.001, 2.0001, 2.00001$ to estimate $\underset{x\to 2^+}{\lim}\frac{|x^2-4|}{x-2}$ .
(These tables are available from a previous Checkpoint problem.)

$\underset{x\to 2^-}{\lim}\frac{|x^2-4|}{x-2}=-4$
latex]\underset{x\to 2^+}{\lim}\frac{|x^2-4|}{x-2}=4[/latex]

Evaluate the one-sided and two-sided limits (if they exist) for the following piecewise function:

$f(x) = \begin{cases} x^2 + 1, & \text{if } x < 2 \ 3x - 5, & \text{if } x \geq 2 \end{cases}$

as $x$ approaches $2$ .

Evaluate the left-hand limit: [

latex] $\begin{array}{rcl} \lim_{x \to 2^-} f(x) &=& \lim_{x \to 2^-} (x^2 + 1) \ &=& 2^2 + 1 \ &=& 5 \end{array}$ [/latex]

Evaluate the right-hand limit:

$\begin{array}{rcl} \lim_{x \to 2^+} f(x) &=& \lim_{x \to 2^+} (3x - 5) \ &=& 3(2) - 5 \ &=& 1 \end{array}$

Since the one-sided limits are not equal ( $5 ≠ 1$ ), the two-sided limit does not exist.

Infinite Limits

The Main Idea

Infinite Limits:
- Occur when function values grow without bound
- Notation: $\lim_{x \to a} f(x) = \pm\infty$
- Infinite limits often indicate discontinuities in functions
One-Sided Infinite Limits:
- Left-hand: $\lim_{x \to a^-} f(x) = \pm\infty$
- Right-hand: $\lim_{x \to a^+} f(x) = \pm\infty$
Vertical Asymptotes:
- Occur where function approaches infinity as x approaches a value
- Line $x = a$ is a vertical asymptote if any of: $\lim_{x \to a^-} f(x) = \pm\infty$ $\lim_{x \to a^+} f(x) = \pm\infty$ $\lim_{x \to a} f(x) = \pm\infty$
Behavior of 1(x−a)n:
- Even $n$ : $\lim_{x \to a} \frac{1}{(x-a)^n} = +\infty$
- Odd $n$ : $\lim_{x \to a^+} \frac{1}{(x-a)^n} = +\infty$ and $\lim_{x \to a^-} \frac{1}{(x-a)^n} = -\infty$

Evaluate each of the following limits, if possible. Use a table of functional values and graph $f(x)=\dfrac{1}{x^2}$ to confirm your conclusion.

$\underset{x\to 0^-}{\lim}\frac{1}{x^2}$
$\underset{x\to 0^+}{\lim}\frac{1}{x^2}$
$\underset{x\to 0}{\lim}\frac{1}{x^2}$

a. $\underset{x\to 0^-}{\lim}\frac{1}{x^2}=+\infty$ ;

b. $\underset{x\to 0^+}{\lim}\frac{1}{x^2}=+\infty$ ;

c. $\underset{x\to 0}{\lim}\frac{1}{x^2}=+\infty$

Evaluate each of the following limits. Identify any vertical asymptotes of the function $f(x)=\dfrac{1}{(x-2)^3}$ .

$\underset{x\to 2^-}{\lim}\dfrac{1}{(x-2)^3}$
$\underset{x\to 2^+}{\lim}\dfrac{1}{(x-2)^3}$
$\underset{x\to 2}{\lim}\dfrac{1}{(x-2)^3}$

a. $\underset{x\to 2^-}{\lim}\frac{1}{(x-2)^3}=−\infty$ ;

b. $\underset{x\to 2^+}{\lim}\frac{1}{(x-2)^3}=+\infty$ ;

c. $\underset{x\to 2}{\lim}\frac{1}{(x-2)^3}$ DNE. The line $x=2$ is the vertical asymptote of $f(x)=\frac{1}{(x-2)^3}$ .

Evaluate $\underset{x\to 1}{\lim}f(x)$ for $f(x)$ shown here:

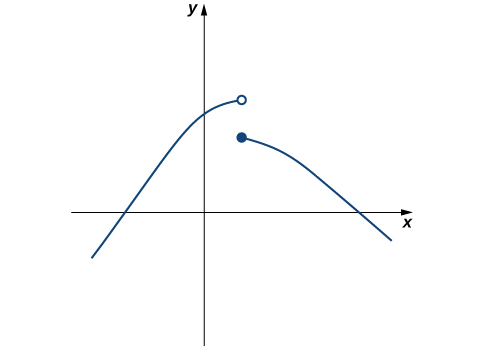
A graph of a piecewise function. The first segment curves from the third quadrant to the first, crossing through the second quadrant. Where the endpoint would be in the first quadrant is an open circle. The second segment starts at a closed circle a few units below the open circle. It curves down from quadrant one to quadrant four. — Figure 11. Graph of a piecewise function