• Determine whether a function is even, odd, or neither

Determine Whether a Functions is Even, Odd, or Neither

Functions often display specific symmetries that define their characteristics. For instance:

• Even Functions
  • A function [latex]f(x)[/latex] is called even if it is symmetric about the [latex]y[/latex]-axis. This means [latex]f(−x)=f(x)[/latex] for all [latex]x[/latex].
  • Graphically, this symmetry means that if the graph of the function is folded along the [latex]y[/latex]-axis, the two halves will match exactly.
  • Examples include [latex]f(x)=x^2[/latex] or [latex]f(x)=∣x∣[/latex], where horizontal reflections produce the original graph.
• Odd Functions
  • A function [latex]f(x)[/latex] is called odd if it has rotational symmetry about the origin, which means [latex]f(−x)=−f(x)[/latex] for all [latex]x[/latex].
  • This property implies that if the function’s graph is rotated [latex]180[/latex] degrees about the origin, it will coincide with its original shape.
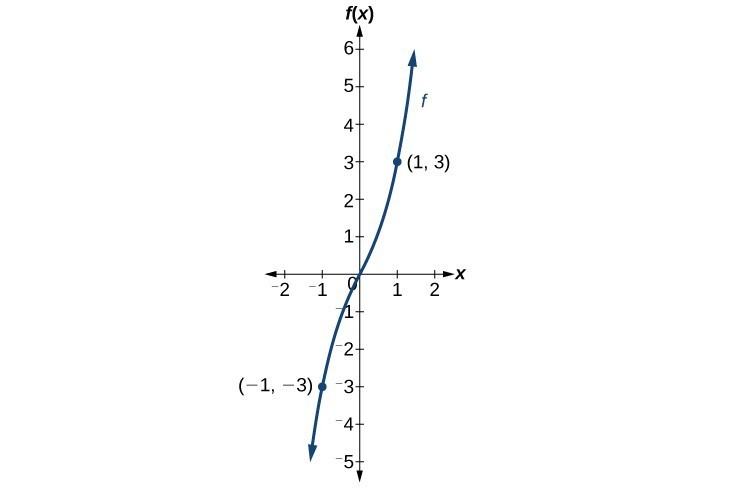
  • An example is [latex]f(x)=x^3[/latex], where reflecting the graph both horizontally and vertically reproduces the original graph.

The function [latex]f(x)=x^3[/latex] demonstrates odd symmetry. As shown in the graphs below:

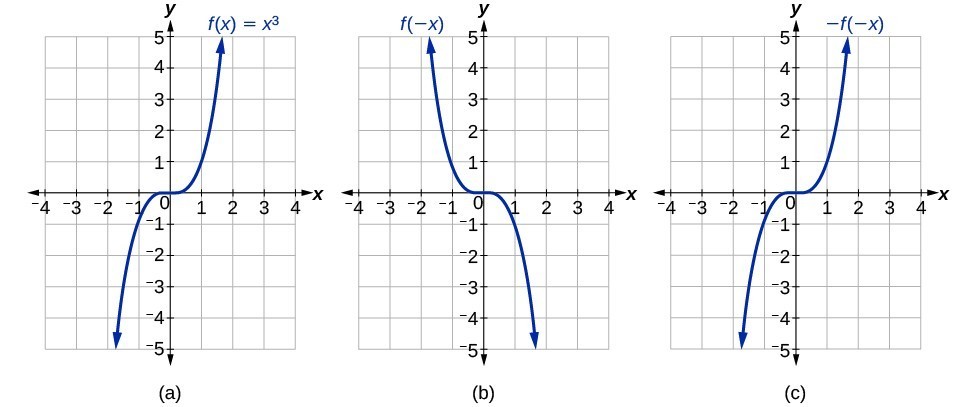
even and odd functions

A function is called an even function if for every input [latex]x[/latex],

 

[latex]f\left(x\right)=f\left(-x\right)[/latex]

 

The graph of an even function is symmetric about the [latex]y\text{-}[/latex] axis.

 

A function is called an odd function if for every input [latex]x[/latex],

 

[latex]f\left(x\right)=-f\left(-x\right)[/latex]

 

The graph of an odd function is symmetric about the origin.

A function can be neither even nor odd if it does not exhibit either symmetry. For example, [latex]f\left(x\right)={2}^{x}[/latex] is neither even nor odd. Also, the only function that is both even and odd is the constant function [latex]f\left(x\right)=0[/latex].

How To: Determine If a Function is Even, Odd, or Neither

• Check for Even Symmetry:
  • Evaluate [latex]f(−x)[/latex] and compare it with [latex]f(x)[/latex]
  • If [latex]f(−x)=f(x)[/latex] for all values of [latex]x[/latex] in the domain of the function, then the function is even.
• Check for Odd Symmetry:
  • Evaluate [latex]f(−x)[/latex] and compare it with [latex]f(x)[/latex]
  • If [latex]f(−x)=−f(x)[/latex] for all values of [latex]x[/latex], then the function is odd.
• Neither Even nor Odd: If neither of the above conditions is met, the function is neither even nor odd.

Is the function [latex]f\left(x\right)={x}^{3}+2x[/latex] even, odd, or neither?

Show Solution

Without looking at a graph, we can determine whether the function is even or odd by finding formulas for the reflections and determining if they return us to the original function. Let’s begin with the rule for even functions.

[latex]f\left(-x\right)={\left(-x\right)}^{3}+2\left(-x\right)=-{x}^{3}-2x[/latex]

This does not return us to the original function, so this function is not even. We can now test the rule for odd functions.

[latex]-f\left(-x\right)=-\left(-{x}^{3}-2x\right)={x}^{3}+2x[/latex]

Because [latex]-f\left(-x\right)=f\left(x\right)[/latex], this is an odd function.

Consider the graph of [latex]f[/latex]. Notice that the graph is symmetric about the origin. For every point [latex]\left(x,y\right)[/latex] on the graph, the corresponding point [latex]\left(-x,-y\right)[/latex] is also on the graph. For example, (1, 3) is on the graph of [latex]f[/latex], and the corresponding point [latex]\left(-1,-3\right)[/latex] is also on the graph.

Is the function [latex]f\left(s\right)={s}^{4}+3{s}^{2}+7[/latex] even, odd, or neither?

Show Solution

Even

You can view the transcript for “Introduction to Odd and Even Functions” here (opens in new window).