Defining the Derivative
For the following exercises (1-5), use the definition of a derivative to find the slope of the secant line between the values [latex]x_1[/latex] and [latex]x_2[/latex] for each function [latex]y=f(x)[/latex].
- [latex]f(x)=4x+7; \,\,\, x_1=2, \,\,\, x_2=5[/latex]
- [latex]f(x)=x^2+2x+1; \,\,\, x_1=3, \,\,\, x_2=3.5[/latex]
- [latex]f(x)=\dfrac{4}{3x-1}; \,\,\, x_1=1, \,\,\, x_2=3[/latex]
- [latex]f(x)=\sqrt{x}; \,\,\, x_1=1, \,\,\, x_2=16[/latex]
- [latex]f(x)=x^{\frac{1}{3}}+1; \,\,\, x_1=0, \,\,\, x_2=8[/latex]
For the following functions (6-10),
- Use [latex]m_{\tan}=\underset{h\to 0}{\lim}\dfrac{f(a+h)-f(a)}{h}[/latex] to find the slope of the tangent line [latex]m_{\tan}=f^{\prime}(a)[/latex], and
- find the equation of the tangent line to [latex]f[/latex] at [latex]x=a[/latex].
- [latex]f(x)=3-4x, \,\,\, a=2[/latex]
- [latex]f(x)=x^2+x, \,\,\, a=1[/latex]
- [latex]f(x)=\dfrac{7}{x}, \,\,\, a=3[/latex]
- [latex]f(x)=2-3x^2, \,\,\, a=-2[/latex]
- [latex]f(x)=\dfrac{2}{x+3}, \,\,\, a=-4[/latex]
For the following functions [latex]y=f(x)[/latex] (11-15), find [latex]f^{\prime}(a)[/latex] using [latex]f^{\prime}(a)=\underset{x\to a}{\lim}\dfrac{f(x)-f(a)}{x-a}[/latex].
- [latex]f(x)=5x+4, \,\,\, a=-1[/latex]
- [latex]f(x)=x^2+9x, \,\,\, a=2[/latex]
- [latex]f(x)=\sqrt{x}, \,\,\, a=4[/latex]
- [latex]f(x)=\dfrac{1}{x}, \,\,\, a=2[/latex]
- [latex]f(x)=\dfrac{1}{x^3}, \,\,\, a=1[/latex]
For the following exercises (16-17), given the function [latex]y=f(x)[/latex],
- find the slope of the secant line [latex]PQ[/latex] for each point [latex]Q(x,f(x))[/latex] with [latex]x[/latex] value given in the table.
- Use the answers from a. to estimate the value of the slope of the tangent line at [latex]P[/latex].
- Use the answer from b. to find the equation of the tangent line to [latex]f[/latex] at point [latex]P[/latex].
- [latex]f(x)=x^2+3x+4, \,\,\, P(1,8)[/latex] (Round to 6 decimal places.)
[latex]x[/latex] Slope [latex]m_{PQ}[/latex] [latex]x[/latex] Slope [latex]m_{PQ}[/latex] [latex]1.1[/latex] (i) [latex]0.9[/latex] (vii) [latex]1.01[/latex] (ii) [latex]0.99[/latex] (viii) [latex]1.001[/latex] (iii) [latex]0.999[/latex] (ix) [latex]1.0001[/latex] (iv) [latex]0.9999[/latex] (x) [latex]1.00001[/latex] (v) [latex]0.99999[/latex] (xi) [latex]1.000001[/latex] (vi) [latex]0.999999[/latex] (xii) - [latex]f(x)=10e^{0.5x}, \,\,\, P(0,10)[/latex] (Round to 4 decimal places.)
[latex]x[/latex] Slope [latex]m_{PQ}[/latex] [latex]-0.1[/latex] (i) [latex]-0.01[/latex] (ii) [latex]-0.001[/latex] (iii) [latex]-0.0001[/latex] (iv) [latex]-0.00001[/latex] (v) [latex]−0.000001[/latex] (vi)
For the following position functions [latex]y=s(t)[/latex] (18-19), an object is moving along a straight line, where [latex]t[/latex] is in seconds and [latex]s[/latex] is in meters. Find
- the simplified expression for the average velocity from [latex]t=2[/latex] to [latex]t=2+h[/latex];
- the average velocity between [latex]t=2[/latex] and [latex]t=2+h[/latex], where (i) [latex]h=0.1[/latex], (ii) [latex]h=0.01[/latex], (iii) [latex]h=0.001[/latex], and (iv) [latex]h=0.0001[/latex]; and
- use the answer from a. to estimate the instantaneous velocity at [latex]t=2[/latex] seconds.
- [latex]s(t)=\frac{1}{3}t+5[/latex]
- [latex]s(t)=2t^3+3[/latex]
For the following exercises (20-21), use the limit definition of derivative to show that the derivative does not exist at [latex]x=a[/latex] for each of the given functions.
- [latex]f(x)=x^{\frac{1}{3}}, \, x=0[/latex]
- [latex]f(x)=\begin{cases} 1 & \text{ if } \, x<1 \\ x & \text{ if } \, x \ge 1 \end{cases}, \, x=1[/latex]
For the following exercises (22-26), complete all parts of each question. You may utilize calculators or any technological aids to facilitate your calculations.
- The position in feet of a race car along a straight track after [latex]t[/latex] seconds is modeled by the function [latex]s(t)=8t^2-\frac{1}{16}t^3[/latex].
- Find the average velocity of the vehicle over the following time intervals to four decimal places:
- [latex][4, 4.1][/latex]
- [latex][4, 4.01][/latex]
- [latex][4, 4.001][/latex]
- [latex][4, 4.0001][/latex]
- Use a. to draw a conclusion about the instantaneous velocity of the vehicle at [latex]t=4[/latex] seconds.
- Find the average velocity of the vehicle over the following time intervals to four decimal places:
- Two vehicles start out traveling side by side along a straight road. Their position functions, shown in the following graph, are given by [latex]s=f(t)[/latex] and [latex]s=g(t)[/latex], where [latex]s[/latex] is measured in feet and [latex]t[/latex] is measured in seconds.

- Which vehicle has traveled farther at [latex]t=2[/latex] seconds?
- What is the approximate velocity of each vehicle at [latex]t=3[/latex] seconds?
- Which vehicle is traveling faster at [latex]t=4[/latex] seconds?
- What is true about the positions of the vehicles at [latex]t=4[/latex] seconds?
- For the function [latex]f(x)=x^3-2x^2-11x+12[/latex], do the following.
- Use a graphing calculator to graph [latex]f[/latex] in an appropriate viewing window.
- Use the ZOOM feature on the calculator to approximate the two values of [latex]x=a[/latex] for which [latex]m_{\tan}=f^{\prime}(a)=0[/latex].
- Suppose that [latex]N(x)[/latex] computes the number of gallons of gas used by a vehicle traveling [latex]x[/latex] miles. Suppose the vehicle gets 30 mpg.
- Find a mathematical expression for [latex]N(x)[/latex].
- What is [latex]N(100)[/latex]? Explain the physical meaning.
- What is [latex]N^{\prime}(100)[/latex]? Explain the physical meaning.
- For the function [latex]f(x)=\dfrac{x^2}{x^2+1}[/latex], do the following.
- Use a graphing calculator to graph [latex]f[/latex] in an appropriate viewing window.
- Use the [latex]\text{nDeriv}[/latex] function on a graphing calculator to find [latex]f^{\prime}(-4), \, f^{\prime}(-2), \, f^{\prime}(2)[/latex], and [latex]f^{\prime}(4)[/latex].
The Derivative as a Function
For the following exercises (1-5), use the definition of a derivative to find [latex]f^{\prime}(x)[/latex].
- [latex]f(x)=2-3x[/latex]
- [latex]f(x)=4x^2[/latex]
- [latex]f(x)=\sqrt{2x}[/latex]
- [latex]f(x)=\dfrac{9}{x}[/latex]
- [latex]f(x)=\dfrac{1}{\sqrt{x}}[/latex]
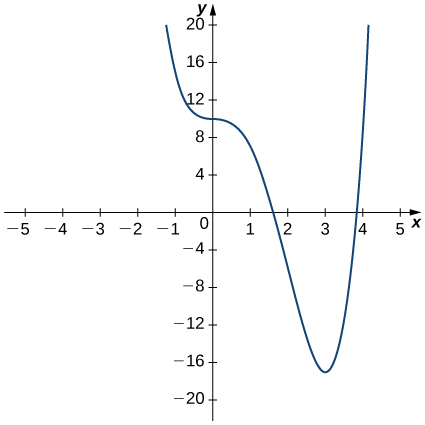
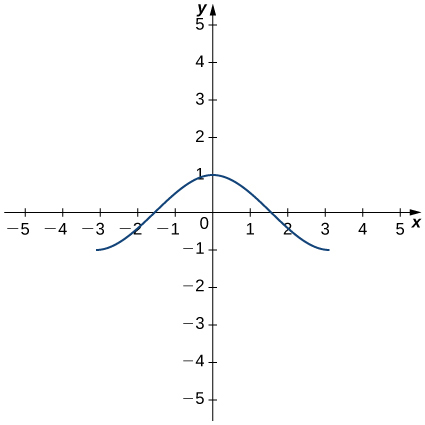
For the following exercises (6-7), use the graph of [latex]y=f(x)[/latex] to sketch the graph of its derivative [latex]f^{\prime}(x)[/latex].
For the following exercises (8-10), the given limit represents the derivative of a function [latex]y=f(x)[/latex] at [latex]x=a[/latex]. Find [latex]f(x)[/latex] and [latex]a[/latex].
- [latex]\underset{h\to 0}{\lim}\dfrac{[3(2+h)^2+2]-14}{h}[/latex]
- [latex]\underset{h\to 0}{\lim}\dfrac{(2+h)^4-16}{h}[/latex]
- [latex]\underset{h\to 0}{\lim}\dfrac{e^h-1}{h}[/latex]
For the following functions (11-12),
- sketch the graph and
- use the definition of a derivative to show that the function is not differentiable at [latex]x=1[/latex].
- [latex]f(x)=\begin{cases} 3 & \text{ if } \, x<1 \\ 3x & \text{ if } \, x \ge 1 \end{cases}[/latex]
- [latex]f(x)=\begin{cases} 2x & \text{ if } x \le 1 \\ \dfrac{2}{x} & \text{ if } \, x>1 \end{cases}[/latex]
For the following functions (13-14), use [latex]f''(x)=\underset{h\to 0}{\lim}\dfrac{f^{\prime}(x+h)-f^{\prime}(x)}{h}[/latex] to find [latex]f''(x)[/latex].
- [latex]f(x)=2-3x[/latex]
- [latex]f(x)=x+\dfrac{1}{x}[/latex]
For the following exercises (15-17), use a calculator to graph [latex]f(x)[/latex]. Determine the function [latex]f^{\prime}(x)[/latex], then use a calculator to graph [latex]f^{\prime}(x)[/latex].
- [latex]f(x)=3x^2+2x+4[/latex]
- [latex]f(x)=\dfrac{1}{\sqrt{2x}}[/latex]
- [latex]f(x)=x^3+1[/latex]
For the following exercises (18-20), describe what the two expressions represent in terms of each of the given situations. Be sure to include units.
- [latex]\dfrac{f(x+h)-f(x)}{h}[/latex]
- [latex]f^{\prime}(x)=\underset{h\to 0}{\lim}\dfrac{f(x+h)-f(x)}{h}[/latex]
- [latex]C(x)[/latex] denotes the total amount of money (in thousands of dollars) spent on concessions by [latex]x[/latex] customers at an amusement park.
- [latex]g(x)[/latex] denotes the grade (in percentage points) received on a test, given [latex]x[/latex] hours of studying.
- [latex]p(x)[/latex] denotes atmospheric pressure at an altitude of [latex]x[/latex] feet.
For the following exercises (21-22), complete all parts of each question. You may utilize calculators or any technological aids to facilitate your calculations.
- Suppose temperature [latex]T[/latex] in degrees Fahrenheit at a height [latex]x[/latex] in feet above the ground is given by [latex]y=T(x)[/latex].
- Give a physical interpretation, with units, of [latex]T^{\prime}(x)[/latex].
- If we know that [latex]{T}^{\prime }(1000)=-0.1,[/latex] explain the physical meaning.
- The graph in the following figure models the number of people [latex]N(t)[/latex] who have come down with the flu [latex]t[/latex] weeks after its initial outbreak in a town with a population of 50,000 citizens.
- Describe what [latex]N^{\prime}(t)[/latex] represents and how it behaves as [latex]t[/latex] increases.
- What does the derivative tell us about how this town is affected by the flu outbreak?

For the following exercises (23-28), use the following table, which shows the height [latex]h[/latex] of the Saturn V rocket for the Apollo 11 mission [latex]t[/latex] seconds after launch.
| Time (seconds) | Height (meters) |
|---|---|
| [latex]0[/latex] | [latex]0[/latex] |
| [latex]1[/latex] | [latex]2[/latex] |
| [latex]2[/latex] | [latex]4[/latex] |
| [latex]3[/latex] | [latex]13[/latex] |
| [latex]4[/latex] | [latex]25[/latex] |
| [latex]5[/latex] | [latex]32[/latex] |
- What is the physical meaning of [latex]h^{\prime}(t)[/latex]? What are the units?
- Construct a table of values for [latex]h^{\prime}(t)[/latex] and graph both [latex]h(t)[/latex] and [latex]h^{\prime}(t)[/latex] on the same graph. (Hint: for interior points, estimate both the left limit and right limit and average them. An interior point of an interval [latex]I[/latex] is an element of [latex]I[/latex] which is not an endpoint of [latex]I[/latex].)
- The best linear fit to the data is given by [latex]H(t)=7.229t-4.905[/latex], where [latex]H[/latex] is the height of the rocket (in meters) and [latex]t[/latex] is the time elapsed since takeoff. From this equation, determine [latex]H^{\prime}(t)[/latex]. Graph [latex]H(t)[/latex] with the given data and, on a separate coordinate plane, graph [latex]H^{\prime}(t)[/latex].
- The best quadratic fit to the data is given by [latex]G(t)=1.429t^2+0.0857t-0.1429[/latex], where [latex]G[/latex] is the height of the rocket (in meters) and [latex]t[/latex] is the time elapsed since takeoff. From this equation, determine [latex]G^{\prime}(t)[/latex]. Graph [latex]G(t)[/latex] with the given data and, on a separate coordinate plane, graph [latex]G^{\prime}(t)[/latex].
- The best cubic fit to the data is given by [latex]F(t)=0.2037t^3+2.956t^2-2.705t+0.4683[/latex], where [latex]F[/latex] is the height of the rocket (in m) and [latex]t[/latex] is the time elapsed since take off. From this equation, determine [latex]F^{\prime}(t)[/latex]. Graph [latex]F(t)[/latex] with the given data and, on a separate coordinate plane, graph [latex]F^{\prime}(t)[/latex]. Does the linear, quadratic, or cubic function fit the data best?
- Using the best linear, quadratic, and cubic fits to the data, determine what [latex]H''(t), \, G''(t)[/latex], and [latex]F''(t)[/latex] are. What are the physical meanings of [latex]H''(t), \, G''(t)[/latex], and [latex]F''(t)[/latex], and what are their units?
Differentiation Rules
For the following exercises (1-6), find [latex]f^{\prime}(x)[/latex] for each function.
- [latex]f(x)=5x^3-x+1[/latex]
- [latex]f(x)=8x^4+9x^2-1[/latex]
- [latex]f(x)=3x\left(18x^4+\dfrac{13}{x+1}\right)[/latex]
- [latex]f(x)=x^2\left(\dfrac{2}{x^2}+\dfrac{5}{x^3}\right)[/latex]
- [latex]f(x)=\dfrac{4x^3-2x+1}{x^2}[/latex]
- [latex]f(x)=\dfrac{x+9}{x^2-7x+1}[/latex]
For the following exercises (7-8), find the equation of the tangent line [latex]T(x)[/latex] to the graph of the given function at the indicated point. Use a graphing calculator to graph the function and the tangent line.
- [latex]y=2\sqrt{x}+1[/latex] at [latex](4,5)[/latex]
- [latex]y=\dfrac{2}{x}-\dfrac{3}{x^2}[/latex] at [latex](1,-1)[/latex]
For the following exercises (9-10), assume that [latex]f(x)[/latex] and [latex]g(x)[/latex] are both differentiable functions for all [latex]x[/latex]. Find the derivative of each of the functions [latex]h(x)[/latex].
- [latex]h(x)=x^3f(x)[/latex]
- [latex]h(x)=\dfrac{3f(x)}{g(x)+2}[/latex]
For the following exercises (11-12), assume that [latex]f(x)[/latex] and [latex]g(x)[/latex] are both differentiable functions with values as given in the following table. Use the following table to calculate the following derivatives.
| [latex]x[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] |
| [latex]f(x)[/latex] | [latex]3[/latex] | [latex]5[/latex] | [latex]-2[/latex] | [latex]0[/latex] |
| [latex]g(x)[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]-4[/latex] | [latex]6[/latex] |
| [latex]f^{\prime}(x)[/latex] | [latex]-1[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]-3[/latex] |
| [latex]g^{\prime}(x)[/latex] | [latex]4[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]9[/latex] |
- Find [latex]h^{\prime}(2)[/latex] if [latex]h(x)=\dfrac{f(x)}{g(x)}[/latex].
- Find [latex]h^{\prime}(4)[/latex] if [latex]h(x)=\dfrac{1}{x}+\dfrac{g(x)}{f(x)}[/latex].
For the following exercises (13-14),
- Evaluate [latex]f^{\prime}(a)[/latex], and
- Graph the function [latex]f(x)[/latex] and the tangent line at [latex]x=a[/latex].
- [latex]f(x)=2x^3+3x-x^2, \,\,\, a=2[/latex]
- [latex]f(x)=x^2-x^{12}+3x+2, \,\,\, a=0[/latex]
For the following exercises (15-21), solve each problem.
- Find the equation of the tangent line to the graph of [latex]f(x)=2x^3+4x^2-5x-3[/latex] at [latex]x=-1[/latex].
- Find the equation of the tangent line to the graph of [latex]f(x)=(3x-x^2)(3-x-x^2)[/latex] at [latex]x=1[/latex].
- Find the equation of the line passing through the point [latex]P(3,3)[/latex] and tangent to the graph of [latex]f(x)=\dfrac{6}{x-1}[/latex].
- Find a quadratic polynomial such that [latex]f(1)=5, \, f^{\prime}(1)=3[/latex], and [latex]f''(1)=-6[/latex].
- A herring swimming along a straight line has traveled [latex]s(t)=\dfrac{t^2}{t^2+2}[/latex] feet in [latex]t[/latex] seconds.
Determine the velocity of the herring when it has traveled [latex]3[/latex] seconds.
- The concentration of antibiotic in the bloodstream [latex]t[/latex] hours after being injected is given by the function [latex]C(t)=\dfrac{2t^2+t}{t^3+50}[/latex], where [latex]C[/latex] is measured in milligrams per liter of blood.
- Find the rate of change of [latex]C(t)[/latex].
- Determine the rate of change for [latex]t=8, \, 12, \, 24[/latex], and [latex]36[/latex].
- Briefly describe what seems to be occurring as the number of hours increases.
- According to Newton’s law of universal gravitation, the force [latex]F[/latex] between two bodies of constant mass [latex]m_1[/latex] and [latex]m_2[/latex] is given by the formula [latex]F=\dfrac{G m_1 m_2}{d^2}[/latex], where [latex]G[/latex] is the gravitational constant and [latex]d[/latex] is the distance between the bodies.
- Suppose that [latex]G, \, m_1[/latex], and [latex]m_2[/latex] are constants. Find the rate of change of force [latex]F[/latex] with respect to distance [latex]d[/latex].
- Find the rate of change of force [latex]F[/latex] with gravitational constant [latex]G=6.67 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2[/latex], on two bodies [latex]10[/latex] meters apart, each with a mass of [latex]1000[/latex] kilograms.
Derivatives as Rates of Change
- The function below represents the position of a particle traveling along a horizontal line.
- Find the velocity and acceleration functions.
- Determine the time intervals when the object is slowing down or speeding up.
[latex]s(t)=2t^3-15t^2+36t-10[/latex]
- A rocket is fired vertically upward from the ground. The distance [latex]s[/latex] in feet that the rocket travels from the ground after [latex]t[/latex] seconds is given by [latex]s(t)=-16t^2+560t[/latex].
- Find the velocity of the rocket [latex]3[/latex] seconds after being fired.
- Find the acceleration of the rocket [latex]3[/latex] seconds after being fired.
- The position function [latex]s(t)=t^2-3t-4[/latex] represents the position of the back of a car backing out of a driveway and then driving in a straight line, where [latex]s[/latex] is in feet and [latex]t[/latex] is in seconds. In this case, [latex]s(t)=0[/latex] represents the time at which the back of the car is at the garage door, so [latex]s(0)=-4[/latex] is the starting position of the car, [latex]4[/latex] feet inside the garage.
- Determine the velocity of the car when [latex]s(t)=0[/latex].
- Determine the velocity of the car when [latex]s(t)=14[/latex].
- A potato is launched vertically upward with an initial velocity of [latex]100 ft/s[/latex] from a potato gun at the top of an [latex]85[/latex]-foot-tall building. The distance in feet that the potato travels from the ground after [latex]t[/latex] seconds is given by [latex]s(t)=-16t^2+100t+85[/latex].
- Find the velocity of the potato after [latex]0.5[/latex] sec and [latex]5.75[latex] sec.
- Find the speed of the potato at [latex]0.5[/latex] sec and [latex]5.75[latex] sec.
- Determine when the potato reaches its maximum height.
- Find the acceleration of the potato at [latex]0.5[/latex] s and [latex]1.5[/latex] s.
- Determine how long the potato is in the air.
- Determine the velocity of the potato upon hitting the ground.
- The following graph shows the position [latex]y=s(t)[/latex] of an object moving along a straight line.

- Use the graph of the position function to determine the time intervals when the velocity is positive, negative, or zero.
- Sketch the graph of the velocity function.
- Use the graph of the velocity function to determine the time intervals when the acceleration is positive, negative, or zero.
- Determine the time intervals when the object is speeding up or slowing down.
- The price [latex]p[/latex] (in dollars) and the demand [latex]x[/latex] for a certain digital clock radio is given by the price-demand function [latex]p=10-0.001x[/latex].
- Find the revenue function [latex]R(x)[/latex].
- Find the marginal revenue function.
- Find the marginal revenue at [latex]x=2000[/latex] and [latex]x=5000[/latex].
- In general, the profit function is the difference between the revenue and cost functions: [latex]P(x)=R(x)-C(x)[/latex].
Suppose the price-demand and cost functions for the production of cordless drills is given respectively by [latex]p=143-0.03x[/latex] and [latex]C(x)=75,000+65x[/latex], where [latex]x[/latex] is the number of cordless drills that are sold at a price of [latex]p[/latex] dollars per drill and [latex]C(x)[/latex] is the cost of producing [latex]x[/latex] cordless drills.
- Find the marginal cost function.
- Find the revenue and marginal revenue functions.
- Find [latex]R^{\prime}(1000)[/latex] and [latex]R^{\prime}(4000)[/latex]. Interpret the results.
- Find the profit and marginal profit functions.
- Find [latex]P^{\prime}(1000)[/latex] and [latex]P^{\prime}(4000)[/latex]. Interpret the results.
- A culture of bacteria grows in number according to the function [latex]N(t)=3000\left(1+\dfrac{4t}{t^2+100}\right)[/latex], where [latex]t[/latex] is measured in hours.
- Find the rate of change of the number of bacteria.
- Find [latex]N^{\prime}(0), \, N^{\prime}(10), \, N^{\prime}(20)[/latex], and [latex]N^{\prime}(30)[/latex].
- Interpret the results in (b).
- Find [latex]N''(0), \, N''(10), \, N''(20)[/latex], and [latex]N''(30)[/latex]. Interpret what the answers imply about the bacteria population growth.