Integrals, Exponential Functions, and Logarithms: Learn It 2

Defining the Number [latex]e[/latex]

Now that we have the natural logarithm defined, we can use that function to define the number [latex]e.[/latex]

the number [latex]e[/latex]

The number [latex]e[/latex] is defined to be the real number such that

[latex]\text{ln}e=1[/latex]

To put it another way, the area under the curve [latex]y=\frac{1}{t}/latex] between [latex]t=1[/latex] and [latex]t=e[/latex] is [latex]1[/latex] (Figure 3).

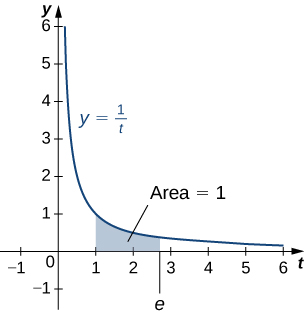
This figure is a graph. It is the curve y=1/t. It is decreasing and in the first quadrant. Under the curve is a shaded area. The area is bounded to the left at x=1 and to the right at x=e. The area is labeled “area=1”.
Figure 3. The area under the curve from 1 to [latex]e[/latex] is equal to one.

The proof that such a number exists and is unique is left to you. (Hint: Use the Intermediate Value Theorem to prove existence and the fact that [latex]\text{ln}x[/latex] is increasing to prove uniqueness.)

The number [latex]e[/latex] can be shown to be irrational, although we won’t do so here. Its approximate value is given by

[latex]e\approx 2.71828182846[/latex]

The Exponential Function

We now turn our attention to the function [latex]{e}^{x}.[/latex] Note that the natural logarithm is one-to-one and therefore has an inverse function. For now, we denote this inverse function by [latex]\text{exp }x.[/latex] Then,

[latex]\text{exp}(\text{ln }x)=x\text{ for }x>0\text{ and }\text{ln}(\text{exp }x)=x\text{ for all }x.[/latex]

The following figure shows the graphs of [latex]\text{exp }x[/latex] and [latex]\text{ln }x.[/latex]

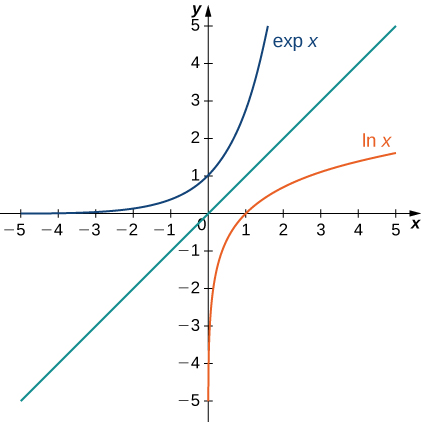
This figure is a graph. It has three curves. The first curve is labeled exp x. It is an increasing curve with the x-axis as a horizontal asymptote. It intersects the y-axis at y=1. The second curve is a diagonal line through the origin. The third curve is labeled lnx. It is an increasing curve with the y-axis as an vertical axis. It intersects the x-axis at x=1.
Figure 4. The graphs of [latex]\text{ln}x[/latex] and [latex]\text{exp}x.[/latex]

We hypothesize that [latex]\text{exp }x={e}^{x}.[/latex]

For rational values of [latex]x,[/latex] this is easy to show. If [latex]x[/latex] is rational, then we have [latex]\text{ln }({e}^{x})=x\text{ln }e=x.[/latex] Thus, when [latex]x[/latex] is rational, [latex]{e}^{x}=\text{exp }x.[/latex]

For irrational values of [latex]x,[/latex] we simply define [latex]{e}^{x}[/latex] as the inverse function of [latex]\text{ln }x.[/latex]

defining the exponential function

For any real number [latex]x,[/latex] define [latex]y={e}^{x}[/latex] to be the number for which

[latex]\text{ln}y=\text{ln}({e}^{x})=x[/latex]

Then we have [latex]{e}^{x}=\text{exp}(x)[/latex] for all [latex]x,[/latex] and thus

[latex]{e}^{\text{ln}x}=x\text{ for }x>0\text{ and }\text{ln}({e}^{x})=x[/latex]

for all [latex]x.[/latex]

Properties of the Exponential Function

Since the exponential function was defined in terms of an inverse function, and not in terms of a power of [latex]e,[/latex] we must verify that the usual laws of exponents hold for the function [latex]{e}^{x}.[/latex]

properties of the exponential function

If [latex]p[/latex] and [latex]q[/latex] are any real numbers and [latex]r[/latex] is a rational number, then

  1. [latex]{e}^{p}{e}^{q}={e}^{p+q}[/latex]
  2. [latex]\frac{{e}^{p}}{{e}^{q}}={e}^{p-q}[/latex]
  3. [latex]{({e}^{p})}^{r}={e}^{pr}[/latex]

Proof

Note that if [latex]p[/latex] and [latex]q[/latex] are rational, the properties hold. However, if [latex]p[/latex] or [latex]q[/latex] are irrational, we must apply the inverse function definition of [latex]{e}^{x}[/latex] and verify the properties. Only the first property is verified here; the other two are left to you. We have

[latex]\text{ln}({e}^{p}{e}^{q})=\text{ln}({e}^{p})+\text{ln}({e}^{q})=p+q=\text{ln}({e}^{p+q}).[/latex]

 

Since [latex]\text{ln}x[/latex] is one-to-one, then

[latex]{e}^{p}{e}^{q}={e}^{p+q}.[/latex]

[latex]_\blacksquare[/latex]

As with part iv. of the logarithm properties, we can extend property iii. to irrational values of [latex]r,[/latex] and we do so by the end of the section.

We also want to verify the differentiation formula for the function [latex]y={e}^{x}.[/latex]

To do this, we need to use implicit differentiation. Let [latex]y={e}^{x}.[/latex] Then,

[latex]\begin{array}{ccc}\hfill \text{ln}y& =\hfill & x\hfill \\ \hfill \frac{d}{dx}\text{ln}y& =\hfill & \frac{d}{dx}x\hfill \\ \hfill \frac{1}{y}\frac{dy}{dx}& =\hfill & 1\hfill \\ \hfill \frac{dy}{dx}& =\hfill & y.\hfill \end{array}[/latex]

Thus, we see

[latex]\frac{d}{dx}{e}^{x}={e}^{x}[/latex]

as desired, which leads immediately to the integration formula

[latex]\displaystyle\int {e}^{x}dx={e}^{x}+C[/latex]

We apply these formulas in the following examples.

Evaluate the following derivatives:

  1. [latex]\frac{d}{dt}{e}^{3t}{e}^{{t}^{2}}[/latex]
  2. [latex]\frac{d}{dx}{e}^{3{x}^{2}}[/latex]

Evaluate the following integral: [latex]\displaystyle\int \frac{4}{{e}^{3x}}dx.[/latex]