Integrals, Exponential Functions, and Logarithms: Learn It 1

  • Understand the natural logarithm and the mathematical constant e using integrals
  • Identify how to differentiate the natural logarithm function
  • Perform integrations where the natural logarithm is involved
  • Understand how to find derivatives and integrals of exponential functions
  • Convert logarithmic and exponential expressions to base e forms

We already examined exponential functions and logarithms in earlier chapters. However, we glossed over some key details in the previous discussions. For example, we did not study how to treat exponential functions with exponents that are irrational. The definition of the number [latex]e[/latex] is another area where the previous development was somewhat incomplete. We now have the tools to deal with these concepts in a more mathematically rigorous way, and we do so in this section.

For purposes of this section, assume we have not yet defined the natural logarithm, the number [latex]e[/latex], or any of the integration and differentiation formulas associated with these functions. 

The Natural Logarithm as an Integral

Recall the power rule for integrals:

[latex]\displaystyle\int {x}^{n}dx=\frac{{x}^{n+1}}{n+1}+C,n\ne \text{−}1.[/latex]

This rule doesn’t work for [latex]n=-1,[/latex] as it would force us to divide by zero. So, how do we integrate [latex]\displaystyle\int \frac{1}{x}dx?[/latex] According to the Fundamental Theorem of Calculus, we know that [latex]{\displaystyle\int }_{1}^{x}\dfrac{1}{t}dt[/latex] is an antiderivative of [latex]\frac{1}{x}.[/latex] 

Therefore, we define the natural logarithm function as follows:

defining the natural logarithm

For [latex]x>0,[/latex] define the natural logarithm function by

[latex]\text{ln}x={\displaystyle\int }_{1}^{x}\frac{1}{t}dt[/latex]

For [latex]x>1,[/latex] this represents the area under the curve [latex]y=\frac{1}{t}[/latex] from [latex]1[/latex] to [latex]x.[/latex] For [latex]x<1,[/latex] we have,

[latex]{\displaystyle\int }_{1}^{x}\frac{1}{t}dt=\text{−}{\displaystyle\int }_{x}^{1}\frac{1}{t}dt,[/latex],

so it is the negative of the area under the curve from [latex]x\text{ to }1[/latex].

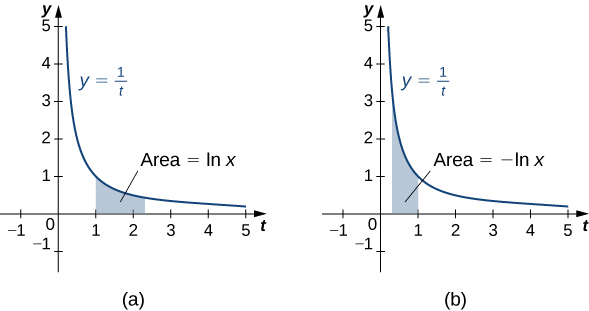
This figure has two graphs. The first is the curve y=1/t. It is decreasing and in the first quadrant. Under the curve is a shaded area. The area is bounded to the left at x=1. The area is labeled “area=lnx”. The second graph is the same curve y=1/t. It has shaded area under the curve bounded to the right by x=1. It is labeled “area=-lnx”.
Figure 1. (a) When [latex]x>1,[/latex] the natural logarithm is the area under the curve [latex]y=\frac{1}{t}[/latex] from [latex]1\text{ to }x.[/latex] (b) When [latex]x<1,[/latex] the natural logarithm is the negative of the area under the curve from [latex]x[/latex] to 1.

Notice that [latex]\text{ln}1=0.[/latex] Furthermore, since [latex]\frac{1}{t} > 0[/latex] for [latex]t > 0[/latex], [latex]\ln x[/latex] is increasing for [latex]x > 0[/latex].

Properties of the Natural Logarithm

Because of the way we defined the natural logarithm, the following differentiation formula falls out immediately as a result of to the Fundamental Theorem of Calculus.

derivative of the natural logarithm

For [latex]x>0,[/latex] the derivative of the natural logarithm is given by

[latex]\frac{d}{dx}\text{ln}x=\dfrac{1}{x}.[/latex]

The function [latex]\text{ln}x[/latex] is differentiable; therefore, it is continuous.

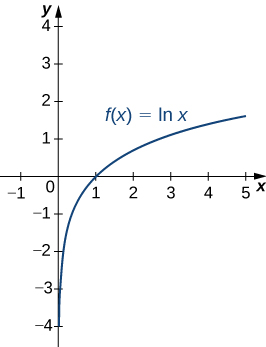
A graph of [latex]\text{ln}x[/latex] is shown below. Notice that it is continuous throughout its domain of [latex](0,\infty ).[/latex]

This figure is a graph. It is an increasing curve labeled f(x)=lnx. The curve is increasing with the y-axis as an asymptote. The curve intersects the x-axis at x=1.
Figure 2. The graph of [latex]f(x)=\text{ln}x[/latex] shows that it is a continuous function.

Calculate the following derivatives:

  1. [latex]\frac{d}{dx}\text{ln}(5{x}^{3}-2)[/latex]
  2. [latex]\frac{d}{dx}{(\text{ln}(3x))}^{2}[/latex]

Note that if we use the absolute value function and create a new function [latex]\text{ln}|x|,[/latex] we can extend the domain of the natural logarithm to include [latex]x<0.[/latex] Then [latex](\frac{d}{dx})\text{ln}|x|=\frac{1}{x}.[/latex] This gives rise to the familiar integration formula.

integral of (1/[latex]u[/latex]) du

The natural logarithm is the antiderivative of the function [latex]f(u)=1\text{/}u\text{:}[/latex]

[latex]\displaystyle\int \frac{1}{u}du=\text{ln}|u|+C[/latex]

Calculate the integral [latex]\displaystyle\int \frac{{x}^{2}}{{x}^{3}+6}dx.[/latex]


Although we have called our function a “logarithm,” we have not actually proved that any of the properties of logarithms hold for this function. We do so here.

properties of the natural logarithm

If [latex]a,b>0[/latex] and [latex]r[/latex] is a rational number, then

  1. [latex]\text{ln}1=0[/latex]
  2. [latex]\text{ln}(ab)=\text{ln}a+\text{ln}b[/latex]
  3. [latex]\text{ln}(\frac{a}{b})=\text{ln}a-\text{ln}b[/latex]
  4. [latex]\text{ln}({a}^{r})=r\text{ln}a[/latex]

Proof

  1. By definition, [latex]\text{ln}1={\displaystyle\int }_{1}^{1}\frac{1}{t}dt=0.[/latex]
  2. We have
    [latex]\text{ln}(ab)={\displaystyle\int }_{1}^{ab}\frac{1}{t}dt={\displaystyle\int }_{1}^{a}\frac{1}{t}dt+{\displaystyle\int }_{a}^{ab}\frac{1}{t}dt.[/latex]

    Use [latex]u\text{-substitution}[/latex] on the last integral in this expression. Let [latex]u=t\text{/}a.[/latex] Then [latex]du=(1\text{/}a)dt.[/latex] Furthermore, when [latex]t=a,u=1,[/latex] and when [latex]t=ab,u=b.[/latex] So we get

    [latex]\text{ln}(ab)={\displaystyle\int }_{1}^{a}\frac{1}{t}dt+{\displaystyle\int }_{a}^{ab}\frac{1}{t}dt={\displaystyle\int }_{1}^{a}\frac{1}{t}dt+{\displaystyle\int }_{1}^{ab}\frac{a}{t}·\frac{1}{a}dt={\displaystyle\int }_{1}^{a}\frac{1}{t}dt+{\displaystyle\int }_{1}^{b}\frac{1}{u}du=\text{ln}a+\text{ln}b.[/latex]

     

  3. Note that
    [latex]\frac{d}{dx}\text{ln}({x}^{r})=\frac{r{x}^{r-1}}{{x}^{r}}=\frac{r}{x}.[/latex]

    Furthermore,

    [latex]\frac{d}{dx}(r\text{ln}x)=\frac{r}{x}.[/latex]

    Since the derivatives of these two functions are the same, by the Fundamental Theorem of Calculus, they must differ by a constant. So we have

    [latex]\text{ln}({x}^{r})=r\text{ln}x+C[/latex]

    for some constant [latex]C.[/latex] Taking [latex]x=1,[/latex] we get

    [latex]\begin{array}{ccc}\hfill \text{ln}({1}^{r})& =\hfill & r\text{ln}(1)+C\hfill \\ \hfill 0& =\hfill & r(0)+C\hfill \\ \hfill C& =\hfill & 0.\hfill \end{array}[/latex]

    Thus [latex]\text{ln}({x}^{r})=r\text{ln}x[/latex] and the proof is complete. Note that we can extend this property to irrational values of [latex]r[/latex] later in this section.
    Part iii. follows from parts ii. and iv. and the proof is left to you.

[latex]_\blacksquare[/latex]

Use properties of logarithms to simplify the following expression into a single logarithm:

[latex]\text{ln}9-2\text{ln}3+\text{ln}(\frac{1}{3})[/latex]