- Use implicit differentiation to find derivatives and the equations for tangent lines
What is Implicit Differentiation?
We have previously explored how to find tangent lines to functions and determine the rate of change of a function at a specific point by explicitly defining the function and its derivatives. However, not all functions can be expressed directly in terms of one variable. Implicit differentiation comes into play when we need to derive functions that are defined implicitly rather than explicitly.
A function is typically described as explicit when the dependent variable [latex]y[/latex] is expressed solely in terms of the independent variable [latex]x[/latex]. For example, [latex]y=x^2+1[/latex] is an explicit function because [latex]y[/latex] is given directly in terms of [latex]x[/latex].
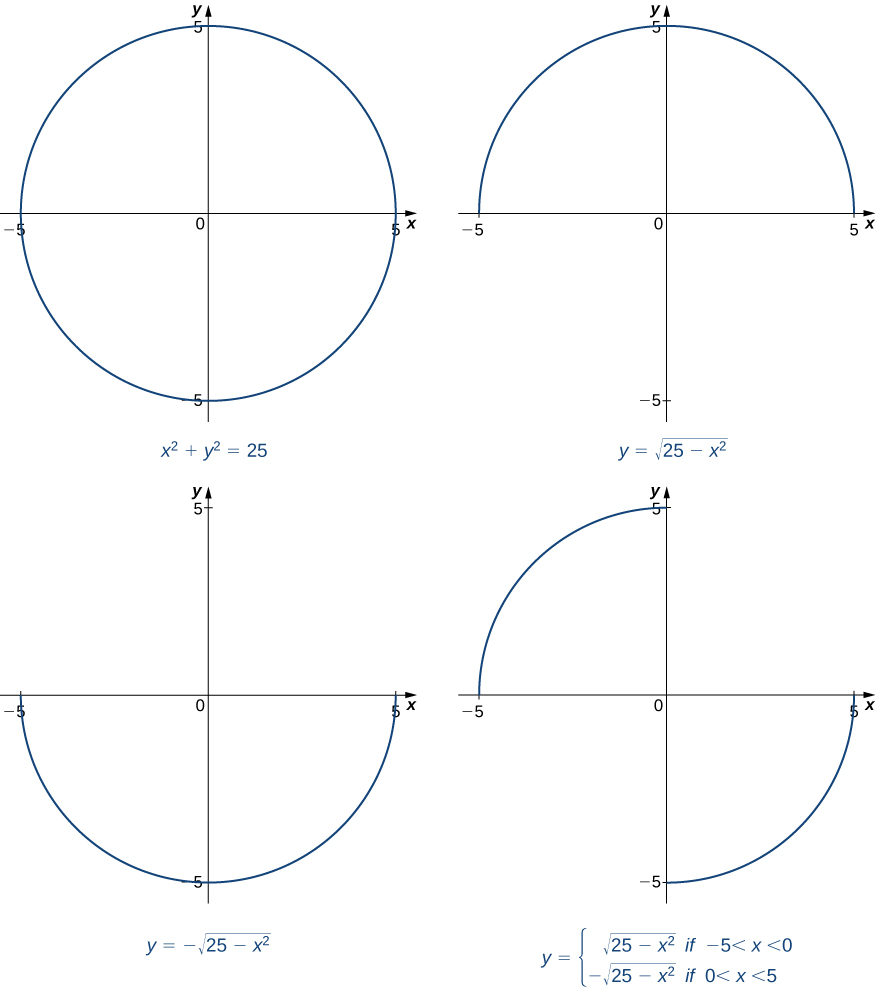
Conversely, if [latex]y[/latex] and [latex]x[/latex] are interrelated through an equation without a straightforward expression of [latex]y[/latex] in terms of [latex]x[/latex], the function is considered an implicit function. An example is the circle equation [latex]x^2 +y^2 =25[/latex], which doesn’t solve for [latex]y[/latex] explicitly in terms of [latex]x[/latex].
Implicit differentiation is essential for finding the slopes of tangent lines to curves that are not explicit functions. For example, the equation [latex]y-x^2=1[/latex] implicitly defines [latex]y[/latex] because it does not isolate [latex]y[/latex] on one side of the equation. This method allows us to derive relations where [latex]y[/latex] is defined implicitly by differentiating both sides of the equation with respect to [latex]x[/latex], treating [latex]y[/latex] as a function of [latex]x[/latex] where necessary.
An equation defines a function implicitly if it holds for [latex]y[/latex] and [latex]x[/latex] without isolating one variable on one side. For instance, the equations:
[latex]y=\sqrt{25-x^2}[/latex], [latex]y = -\sqrt{25-x^2}[/latex], and [latex]y=\begin{cases} \sqrt{25-x^2} & \text{ if } \, -5 \le x < 0 \\ -\sqrt{25-x^2} & \text{ if } \, 0 \le x \le 5 \end{cases}[/latex],
are all examples of functions defined implicitly by the circle equation [latex]x^2+y^2=25[/latex].
Figure 1 illustrates how the equation [latex]x^2+y^2=25[/latex] defines multiple functions implicitly, showcasing different ways [latex]y[/latex] can be expressed in relation to [latex]x[/latex]. These representations include the full circle and its segments, dependent on [latex]x[/latex] values, demonstrating the versatility of implicit functions.
To apply implicit differentiation practically, consider finding the slope of the tangent line to the circle at a specific point.
For example, to determine the slope at point [latex](3,4)[/latex], one might initially think to differentiate [latex]y=\sqrt{25-x^2}[/latex] directly at [latex]x=3[/latex]. Similarly, to find the slope at [latex](3,-4)[/latex], we could use the derivative of [latex]y=−\sqrt{25-x^2}[/latex]. However, these expressions don’t always provide the clearest path for differentiation, especially over different ranges of [latex]x[/latex].
Implicit differentiation streamlines this process by differentiating the entire equation directly:
[latex]2x+2y \frac{dy}{dx}=0[/latex]
This leads to:
[latex]\frac{dy}{dx}=\frac{-x}{y}[/latex]
which can then be evaluated at any point on the curve without having to solve explicitly for [latex]y[/latex] first. This method confirms the flexibility and power of implicit differentiation in handling equations where [latex]y[/latex] is not isolated.
The process of finding [latex]\frac{dy}{dx}[/latex] using implicit differentiation is described in the following problem-solving strategy.
Problem-Solving Strategy: Implicit Differentiation
To perform implicit differentiation on an equation that defines a function [latex]y[/latex] implicitly in terms of a variable [latex]x[/latex], use the following steps:
- Take the derivative of both sides of the equation. Keep in mind that [latex]y[/latex] is a function of [latex]x[/latex]. Consequently, whereas [latex]\frac{d}{dx}(\sin x)= \cos x, \, \frac{d}{dx}(\sin y)= \cos y\frac{dy}{dx}[/latex] because we must use the Chain Rule to differentiate [latex]\sin y[/latex] with respect to [latex]x[/latex].
- Rewrite the equation so that all terms containing [latex]\frac{dy}{dx}[/latex] are on the left and all terms that do not contain [latex]\frac{dy}{dx}[/latex] are on the right.
- Factor out [latex]\frac{dy}{dx}[/latex] on the left.
- Solve for [latex]\frac{dy}{dx}[/latex] by dividing both sides of the equation by an appropriate algebraic expression.
Assuming that [latex]y[/latex] is defined implicitly by the equation [latex]x^2+y^2=25[/latex], find [latex]\frac{dy}{dx}[/latex].
Assuming that [latex]y[/latex] is defined implicitly by the equation [latex]x^3 \sin y+y=4x+3[/latex], find [latex]\frac{dy}{dx}[/latex].
Find [latex]\frac{d^2 y}{dx^2}[/latex] if [latex]x^2+y^2=25[/latex].