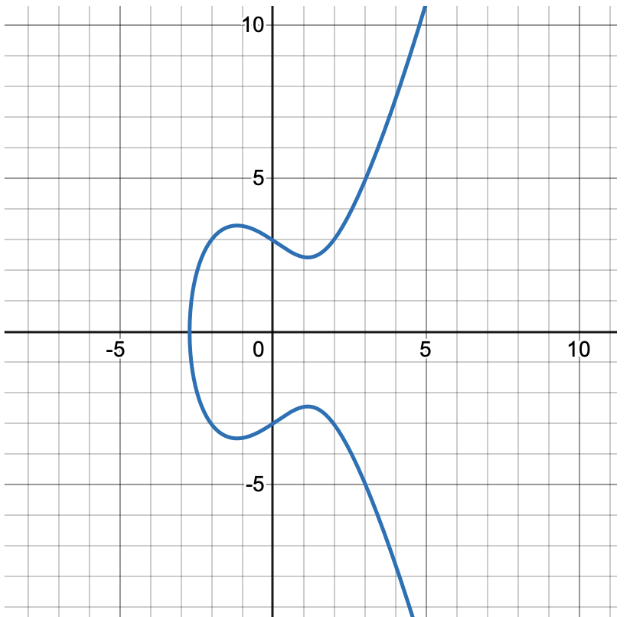
- Use implicit differentiation to find derivatives and the equations for tangent lines
Elliptic Curve Cryptography: Exploring the Mathematics Behind Secure Communication
Elliptic Curve Cryptography (ECC) has emerged as a powerful tool in the realm of secure communication, offering advantages in efficiency and security over traditional methods. This cryptographic approach, utilized in technologies like Bitcoin, relies on the complex mathematical properties of elliptic curves. Unlike simpler functions, elliptic curves are often more manageable when expressed implicitly rather than explicitly. This characteristic makes them particularly useful for creating secure encryption systems, as they provide robust security with relatively small key sizes.
In this apply-it task, we’ll delve into the mathematical foundations of ECC by examining a specific elliptic curve. We’ll explore how to find derivatives using implicit differentiation, calculate slopes of tangent lines at given points, and determine equations of these tangent lines.