The Washer Method
Some solids of revolution have cavities in the middle; they are not solid all the way to the axis of revolution. This can happen because of the shape of the region of revolution with respect to the axis. Cavities also arise when the region of revolution is defined between the graphs of two functions or [latex]x[/latex]-axis or [latex]y[/latex]-axis is selected for revolution.
When the solid of revolution has a cavity, the slices used to approximate the volume are not disks but washers (disks with holes in the center).
For example, consider the region bounded above by the graph of the function [latex]f(x)=\sqrt{x}[/latex] and below by the graph of the function [latex]g(x)=1[/latex] over the interval [latex]\left[1,4\right].[/latex] When this region is revolved around the [latex]x\text{-axis,}[/latex] the result is a solid with a cavity in the middle, and the slices are washers.

The cross-sectional area, then, is the area of the outer circle less the area of the inner circle. In this case,
Then the volume of the solid is:
Generalizing this process gives the washer method.
the washer method
Suppose [latex]f(x)[/latex] and [latex]g(x)[/latex] are continuous, nonnegative functions such that [latex]f(x)\ge g(x)[/latex] over [latex]\left[a,b\right].[/latex]
Let [latex]R[/latex] denote the region bounded above by the graph of [latex]f(x),[/latex] below by the graph of [latex]g(x),[/latex] on the left by the line [latex]x=a,[/latex] and on the right by the line [latex]x=b.[/latex]
Then, the volume of the solid of revolution formed by revolving [latex]R[/latex] around the [latex]x\text{-axis}[/latex] is given by:
Find the volume of a solid of revolution formed by revolving the region bounded above by the graph of [latex]f(x)=x[/latex] and below by the graph of [latex]g(x)=\frac{1}{x}[/latex] over the interval [latex]\left[1,4\right][/latex] around the [latex]x\text{-axis}\text{.}[/latex]
As with the disk method, we can also apply the washer method to solids of revolution that result from revolving a region around the [latex]y[/latex]-axis. In this case, the following rule applies.
the washer method for solids of revolution around the [latex]y[/latex]-axis
Suppose [latex]u(y)[/latex] and [latex]v(y)[/latex] are continuous, nonnegative functions such that [latex]v(y)\le u(y)[/latex] for [latex]y\in \left[c,d\right].[/latex]
Let [latex]Q[/latex] denote the region bounded on the right by the graph of [latex]u(y),[/latex] on the left by the graph of [latex]v(y),[/latex] below by the line [latex]y=c,[/latex] and above by the line [latex]y=d.[/latex]
Then, the volume of the solid of revolution formed by revolving [latex]Q[/latex] around the [latex]y\text{-axis}[/latex] is given by:
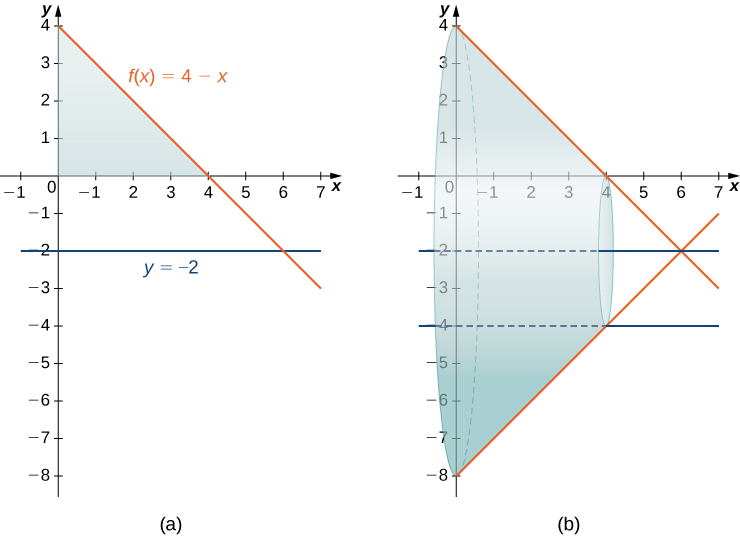
Rather than looking at an example of the washer method with the [latex]y\text{-axis}[/latex] as the axis of revolution, we now consider an example in which the axis of revolution is a line other than one of the two coordinate axes. The same general method applies, but you may have to visualize just how to describe the cross-sectional area of the volume.
An important thing to remember is that for both the disk and washer method, the rectangles (the radii of the cross-sectional circles) are always perpendicular to the axis of revolution.
Find the volume of a solid of revolution formed by revolving the region bounded above by [latex]f(x)=4-x[/latex] and below by the [latex]x\text{-axis}[/latex] over the interval [latex]\left[0,4\right][/latex] around the line [latex]y=-2.[/latex]