Derivatives of Exponential and Logarithmic Functions: Learn It 2

Derivative of the Logarithmic Function

Now that we have the derivative of the natural exponential function, we can use implicit differentiation to find the derivative of its inverse, the natural logarithmic function.

derivative of the natural logarithmic function

If [latex]x>0[/latex] and [latex]y=\ln x[/latex], then

[latex]\frac{dy}{dx}=\dfrac{1}{x}[/latex]

 

More generally, let [latex]g(x)[/latex] be a differentiable function. For all values of [latex]x[/latex] for which [latex]g^{\prime}(x)>0[/latex], the derivative of [latex]h(x)=\ln(g(x))[/latex] is given by

[latex]h^{\prime}(x)=\dfrac{1}{g(x)} g^{\prime}(x)[/latex]

Proof

If [latex]x>0[/latex] and [latex]y=\ln x[/latex], then [latex]e^y=x[/latex]. Differentiating both sides of this equation results in the equation

[latex]e^y\frac{dy}{dx}=1[/latex]

 

Solving for [latex]\frac{dy}{dx}[/latex] yields

[latex]\frac{dy}{dx}=\dfrac{1}{e^y}[/latex]

 

Finally, we substitute [latex]x=e^y[/latex] to obtain

[latex]\frac{dy}{dx}=\dfrac{1}{x}[/latex]

 

We may also derive this result by applying the inverse function theorem, as follows. Since [latex]y=g(x)=\ln x[/latex] is the inverse of [latex]f(x)=e^x[/latex], by applying the inverse function theorem we have

[latex]\frac{dy}{dx}=\dfrac{1}{f^{\prime}(g(x))}=\dfrac{1}{e^{\ln x}}=\dfrac{1}{x}[/latex]

 

Using this result and applying the chain rule to [latex]h(x)=\ln(g(x))[/latex] yields

[latex]h^{\prime}(x)=\dfrac{1}{g(x)} g^{\prime}(x)[/latex]

[latex]_\blacksquare[/latex]

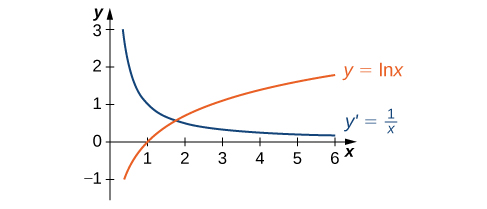
The graph of [latex]y=\ln x[/latex] and its derivative [latex]\frac{dy}{dx}=\frac{1}{x}[/latex] are shown in Figure 3.

Graph of the function ln x along with its derivative 1/x. The function ln x is increasing on (0, + ∞). Its derivative is decreasing but greater than 0 on (0, + ∞).
Figure 3. The function [latex]y=\ln x[/latex] is increasing on [latex](0,+\infty)[/latex]. Its derivative [latex]y^{\prime} =\frac{1}{x}[/latex] is greater than zero on [latex](0,+\infty)[/latex].

Find the derivative of [latex]f(x)=\ln(x^3+3x-4)[/latex]

Find the derivative of [latex]f(x)=\ln\left(\dfrac{x^2 \sin x}{2x+1}\right)[/latex]

Now that we can differentiate the natural logarithmic function, we can use this result to find the derivatives of [latex]y=\log_b x[/latex] and [latex]y=b^x[/latex] for [latex]b>0, \, b\ne 1[/latex].

derivatives of general exponential and logarithmic functions

Let [latex]b>0, \, b\ne 1[/latex], and let [latex]g(x)[/latex] be a differentiable function.

  1. If [latex]y=\log_b x[/latex], then
    [latex]\frac{dy}{dx}=\dfrac{1}{x \ln b}[/latex]

    More generally, if [latex]h(x)=\log_b (g(x))[/latex], then for all values of [latex]x[/latex] for which [latex]g(x)>0[/latex],

    [latex]h^{\prime}(x)=\dfrac{g^{\prime}(x)}{g(x) \ln b}[/latex]

  2. If [latex]y=b^x[/latex], then
    [latex]\frac{dy}{dx}=b^x \ln b[/latex]

    More generally, if [latex]h(x)=b^{g(x)}[/latex], then

    [latex]h^{\prime}(x)=b^{g(x)} g^{\prime}(x) \ln b[/latex]

Proof

If [latex]y=\log_b x[/latex], then [latex]b^y=x[/latex]. It follows that [latex]\ln(b^y)=\ln x[/latex]. Thus [latex]y \ln b = \ln x[/latex]. Solving for [latex]y[/latex], we have [latex]y=\frac{\ln x}{\ln b}[/latex]. Differentiating and keeping in mind that [latex]\ln b[/latex] is a constant, we see that

[latex]\frac{dy}{dx}=\dfrac{1}{x \ln b}[/latex]

 

The derivative from above now follows from the chain rule.

If [latex]y=b^x[/latex], then [latex]\ln y=x \ln b[/latex]. Using implicit differentiation, again keeping in mind that [latex]\ln b[/latex] is constant, it follows that [latex]\frac{1}{y}\frac{dy}{dx}=\text{ln}b.[/latex] Solving for [latex]\frac{dy}{dx}[/latex] and substituting [latex]y=b^x[/latex], we see that

[latex]\frac{dy}{dx}=y \ln b=b^x \ln b[/latex]

 

The more general derivative follows from the chain rule.

[latex]_\blacksquare[/latex]

Find the derivative of [latex]h(x)= \dfrac{3^x}{3^x+2}[/latex]

Find the slope of the line tangent to the graph of [latex]y=\log_2 (3x+1)[/latex] at [latex]x=1[/latex].