One of the most commonly described phenomena using exponential and logarithmic functions is growth.  Both exponential and logarithmic functions increase without bound, but the rate at which that happens for each function is different.

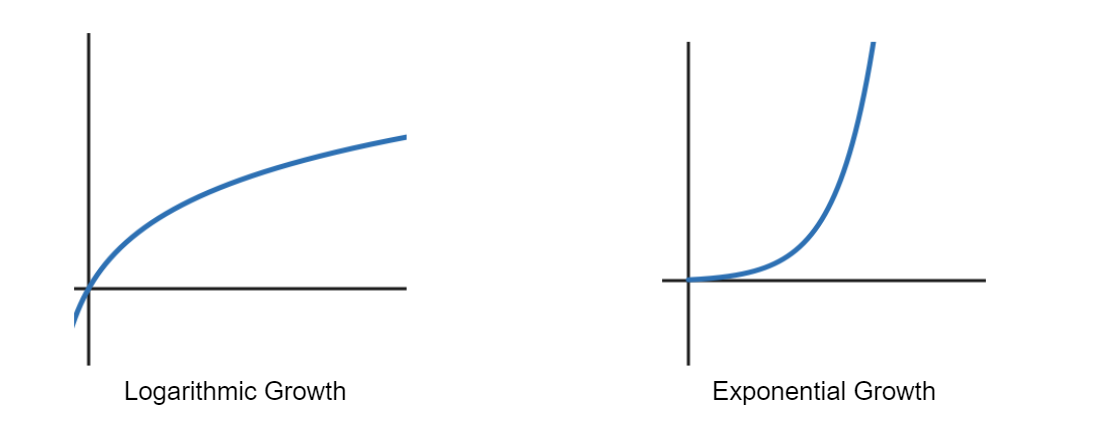
Exponential growth starts off slow and gets faster and faster.  For instance, the amount of traffic a website gets is slow at first, but as more people visit, word spreads and search engines start recommending the site, the number of visits become greater and greater. 

​​On the other hand, logarithmic growth increases very quickly at the beginning but slows down as time goes on. For instance, when you begin a strength training journey you often see large gains right away, but as the journey goes on the gains become smaller or farther apart, so the rate slows down.