Types of Discontinuities
As we have seen in the earlier examples, discontinuities take on several different appearances. We classify the types of discontinuities we have seen thus far as removable discontinuities, infinite discontinuities, or jump discontinuities.
- A removable discontinuity is a discontinuity for which there is a hole in the graph
- A jump discontinuity is a noninfinite discontinuity for which the sections of the function do not meet up
- An infinite discontinuity is a discontinuity located at a vertical asymptote.
The figure below illustrates the differences in these types of discontinuities.
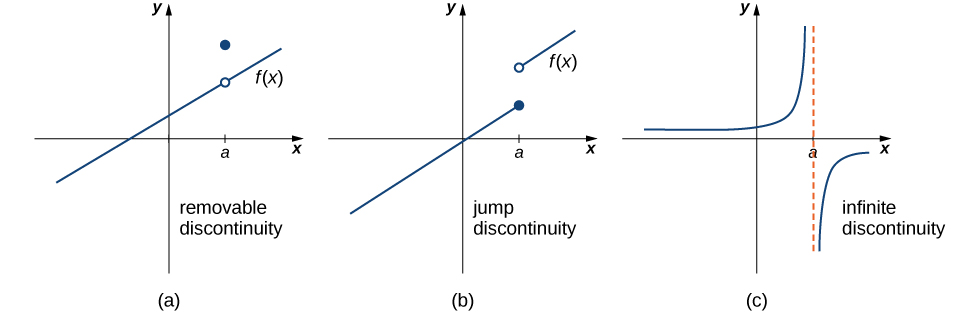
These three discontinuities are formally defined as follows:
types of discontinuities
If [latex]f(x)[/latex] is discontinuous at [latex]a[/latex], then
- [latex]f[/latex] has a removable discontinuity at [latex]a[/latex] if [latex]\underset{x\to a}{\lim}f(x)[/latex] exists.
(Note: When we state that [latex]\underset{x\to a}{\lim}f(x)[/latex] exists, we mean that [latex]\underset{x\to a}{\lim}f(x)=L[/latex], where [latex]L[/latex] is a real number.) - [latex]f[/latex] has a jump discontinuity at [latex]a[/latex] if [latex]\underset{x\to a^-}{\lim}f(x)[/latex] and [latex]\underset{x\to a^+}{\lim}f(x)[/latex] both exist, but [latex]\underset{x\to a^-}{\lim}f(x)\ne \underset{x\to a^+}{\lim}f(x)[/latex].
(Note: When we state that [latex]\underset{x\to a^-}{\lim}f(x)[/latex] and [latex]\underset{x\to a^+}{\lim}f(x)[/latex] both exist, we mean that both are real-valued and that neither take on the values [latex]\pm \infty[/latex].) - [latex]f[/latex] has an infinite discontinuity at [latex]a[/latex] if [latex]\underset{x\to a^-}{\lim}f(x)=\pm \infty[/latex] or [latex]\underset{x\to a^+}{\lim}f(x)=\pm \infty[/latex].
Although these terms provide a handy way of describing three common types of discontinuities, keep in mind that not all discontinuities fit neatly into these categories.
In an earlier example, we showed that [latex]f(x)=\dfrac{x^2-4}{x-2}[/latex] is discontinuous at [latex]x=2[/latex]. Classify this discontinuity as removable, jump, or infinite.
In an earlier example, we showed that [latex]f(x)=\begin{cases} -x^2+4 & \text{ if } \, x \le 3 \\ 4x-8 & \text{ if } \, x > 3 \end{cases}[/latex] is discontinuous at [latex]x=3[/latex]. Classify this discontinuity as removable, jump, or infinite.
Determine whether [latex]f(x)=\dfrac{x+2}{x+1}[/latex] is continuous at [latex]−1[/latex]. If the function is discontinuous at [latex]−1[/latex], classify the discontinuity as removable, jump, or infinite.