Continuity: Learn It 1

  • Outline the three criteria a function must meet to be continuous at a specific point
  • Explain the different types of breaks a function can have that make it not continuous
  • Explain what it means for a function to be continuous over a range of values
  • Explain the rule for calculating limits of functions that are combined
  • Show how a continuous function reaches every value between its start and end points using the Intermediate Value Theorem

Continuity

Many functions can be traced without lifting your pencil, indicating they are continuous. Functions that cannot be traced this way have points of discontinuity. To understand continuity at a point, consider the following conditions:

  1. The function [latex]f(a)[/latex] is defined:

    • The function must have a value at [latex]a[/latex].

  2. The limit [latex]\underset{x\to a}{\lim}f(x)[/latex] exists:

    • The value that [latex]f(x)[/latex] approaches as [latex]x[/latex] gets closer to [latex]a[/latex] must exist.

  3. The limit equals the function value [latex]\underset{x\to a}{\lim}f(x)=f(a)[/latex]:

    • The value that [latex]f(x)[/latex] approaches must be the same as the value of the function at [latex]a[/latex].

Let’s illustrate these conditions:

  • Undefined Function:

    • If [latex]f(a)[/latex] is not defined, the function is not continuous at [latex]a[/latex].
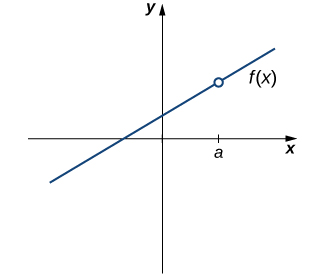
      A graph of an increasing linear function f(x) which crosses the x axis from quadrant three to quadrant two and which crosses the y axis from quadrant two to quadrant one. A point a greater than zero is marked on the x axis. The point on the function f(x) above a is an open circle; the function is not defined at a.
      Figure 1. The function [latex]f(x)[/latex] is not continuous at a because [latex]f(a)[/latex] is undefined.

  • Non-existent Limit:

    • Even if [latex]f(a)[/latex] is defined, if [latex]\underset{x\to a}{\lim}f(x)[/latex] does not exist, the function is not continuous at [latex]a[/latex].
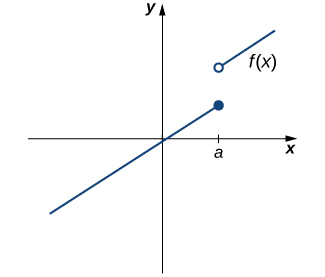
      The graph of a piecewise function f(x) with two parts. The first part is an increasing linear function that crosses from quadrant three to quadrant one at the origin. A point a greater than zero is marked on the x axis. At fa. on this segment, there is a solid circle. The other segment is also an increasing linear function. It exists in quadrant one for values of x greater than a. At x=a, this segment has an open circle.
      Figure 2. The function [latex]f(x)[/latex] is not continuous at a because [latex]\underset{x\to a}{\lim}f(x)[/latex] does not exist.

  • Limit Not Equal to Function Value:

    • If [latex]f(a)[/latex] is defined and [latex]\underset{x\to a}{\lim}f(x)[/latex] exists, but they are not equal, the function is not continuous at [latex]a[/latex].
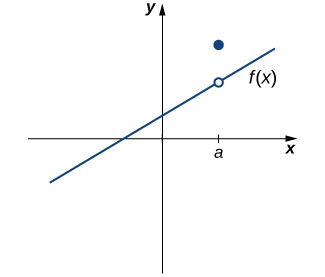
      The graph of a piecewise function with two parts. The first part is an increasing linear function that crosses the x axis from quadrant three to quadrant two and which crosses the y axis from quadrant two to quadrant one. A point a greater than zero is marked on the x axis. At this point, there is an open circle on the linear function. The second part is a point at x=a above the line.
      Figure 3. The function [latex]f(x)[/latex] is not continuous at a because [latex]\underset{x\to a}{\lim}f(x)\ne f(a)[/latex].

continuity

A function [latex]f(x)[/latex] is continuous at a point [latex]a[/latex] if and only if the following three conditions are satisfied:

  1. [latex]f(a)[/latex] is defined
  2. [latex]\underset{x\to a}{\lim}f(x)[/latex] exists
  3. [latex]\underset{x\to a}{\lim}f(x)=f(a)[/latex]

A function is discontinuous at a point [latex]a[/latex] if it fails to be continuous at [latex]a[/latex].

The following procedure can be used to analyze the continuity of a function at a point using this definition.

How to: Determine Continuity at a Point

  1. Check to see if [latex]f(a)[/latex] is defined.
    • If [latex]f(a)[/latex] is undefined, we need go no further. The function is not continuous at [latex]a[/latex].
    • If [latex]f(a)[/latex] is defined, continue to step 2.
  2. Compute [latex]\underset{x\to a}{\lim}f(x)[/latex]. In some cases, we may need to do this by first computing [latex]\underset{x\to a^-}{\lim}f(x)[/latex] and [latex]\underset{x\to a^+}{\lim}f(x)[/latex].
    • If [latex]\underset{x\to a}{\lim}f(x)[/latex] does not exist (that is, it is not a real number), then the function is not continuous at [latex]a[/latex].
    • If [latex]\underset{x\to a}{\lim}f(x)[/latex] exists, then continue to step 3.
  3. Compare [latex]f(a)[/latex] and [latex]\underset{x\to a}{\lim}f(x)[/latex].
    • If [latex]\underset{x\to a}{\lim}f(x)\ne f(a)[/latex], then the function is not continuous at [latex]a[/latex].
    • If [latex]\underset{x\to a}{\lim}f(x)=f(a)[/latex], then the function is continuous at [latex]a[/latex].

The next three examples demonstrate how to apply this definition to determine whether a function is continuous at a given point. These examples illustrate situations in which each of the conditions for continuity in the definition succeed or fail.

Using the definition, determine whether the function [latex]f(x)=\dfrac{(x^2-4)}{(x-2)}[/latex] is continuous at [latex]x=2[/latex]. Justify the conclusion.

Using the definition, determine whether the function [latex]f(x)=\begin{cases} -x^2+4 & \text{ if } \, x \le 3 \\ 4x-8 & \text{ if } \, x > 3 \end{cases}[/latex] is continuous at [latex]x=3[/latex]. Justify the conclusion.

Using the definition, determine whether the function [latex]f(x)=\begin{cases} \frac{\sin x}{x} & \text{ if } \, x \ne 0 \\ 1 & \text{ if } \, x = 0 \end{cases}[/latex] is continuous at [latex]x=0[/latex].

Watch the following video to see the worked solutions to the three previous examples.


By applying the definition of continuity and previously established theorems concerning the evaluation of limits, we can state the following theorem.

continuity of polynomials and rational functions

Polynomials and rational functions are continuous at every point in their domains.

Proof

Previously, we showed that if [latex]p(x)[/latex] and [latex]q(x)[/latex] are polynomials, [latex]\underset{x\to a}{\lim}p(x)=p(a)[/latex] for every polynomial [latex]p(x)[/latex] and [latex]\underset{x\to a}{\lim}\dfrac{p(x)}{q(x)}=\dfrac{p(a)}{q(a)}[/latex] as long as [latex]q(a)\ne 0[/latex]. Therefore, polynomials and rational functions are continuous on their domains.

[latex]_\blacksquare[/latex]

The domain of every polynomial function is all real numbers. 

The domain of a rational functional can be found by:

  1. Set the denominator equal to zero.
  2. Solve to find the values of the variable that cause the denominator to equal zero.
  3. The domain contains all real numbers except those found in Step 2.

We now apply continuity of polynomials and rational functions to determine the points at which a given rational function is continuous.

For what values of [latex]x[/latex] is [latex]f(x)=\dfrac{x+1}{x-5}[/latex] continuous?