Contextual Applications of Derivatives: Get Stronger

Limits at Infinity and Asymptotes

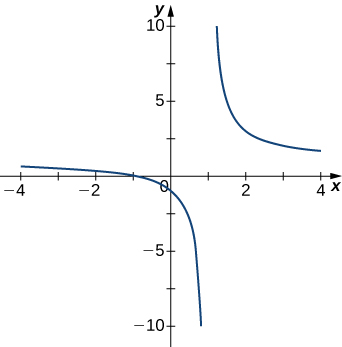
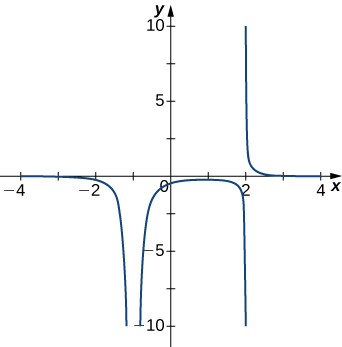
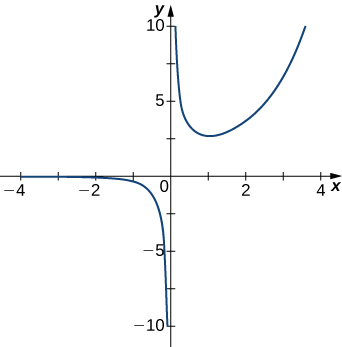
For the following exercises (1-3), examine the graphs. Identify where the vertical asymptotes are located.

  1. The function graphed decreases very rapidly as it approaches x = 1 from the left, and on the other side of x = 1, it seems to start near infinity and then decrease rapidly.
  2. The function graphed decreases very rapidly as it approaches x = −1 from the left, and on the other side of x = −1, it seems to start near negative infinity and then increase rapidly to form a sort of U shape that is pointing down, with the other side of the U being at x = 2. On the other side of x = 2, the graph seems to start near infinity and then decrease rapidly.
  3.  The function graphed decreases very rapidly as it approaches x = 0 from the left, and on the other side of x = 0, it seems to start near infinity and then decrease rapidly to form a sort of U shape that is pointing up, with the other side being a normal function that appears as if it will take the entirety of the values of the x-axis.

For the following functions [latex]f(x)[/latex] (4-5), determine whether there is an asymptote at [latex]x=a[/latex]. Justify your answer without graphing on a calculator.

  1. [latex]f(x)=\dfrac{x}{x-2}, \, a=2[/latex]
  2. [latex]f(x)=(x-1)^{-1/3}, \, a=1[/latex]

For the following exercises (6-10), evaluate the limit.

  1. [latex]\underset{x\to \infty }{\lim}\dfrac{1}{3x+6}[/latex]
  2. [latex]\underset{x\to \infty }{\lim}\dfrac{x^2-2x+5}{x+2}[/latex]
  3. [latex]\underset{x\to −\infty }{\lim}\dfrac{x^4-4x^3+1}{2-2x^2-7x^4}[/latex]
  4. [latex]\underset{x\to −\infty }{\lim}\dfrac{\sqrt{4x^2-1}}{x+2}[/latex]
  5. [latex]\underset{x\to −\infty }{\lim}\dfrac{4x}{\sqrt{x^2-1}}[/latex]

For the following exercises (11-17), find the horizontal and vertical asymptotes.

  1. [latex]f(x)=x-\dfrac{9}{x}[/latex]
  2. [latex]f(x)=\dfrac{x^3}{4-x^2}[/latex]
  3. [latex]f(x)= \sin (x) \sin (2x)[/latex]
  4. [latex]f(x)=\dfrac{x \sin (x)}{x^2-1}[/latex]
  5. [latex]f(x)=\dfrac{1}{x^3+x^2}[/latex]
  6. [latex]f(x)=\dfrac{x^3+1}{x^3-1}[/latex]
  7. [latex]f(x)=x- \sin x[/latex]

For the following exercises (18-19), construct a function [latex]f(x)[/latex] that has the given asymptotes.

  1. [latex]x=1[/latex] and [latex]y=2[/latex]
  2. [latex]y=4[/latex] and [latex]x=-1[/latex]

For the following exercises (20-22), graph the function on a graphing calculator on the window [latex]x=[-5,5][/latex] and estimate the horizontal asymptote or limit. Then, calculate the actual horizontal asymptote or limit.

  1. [latex]f(x)=\dfrac{1}{x+10}[/latex]
  2. [latex]\underset{x\to −\infty }{\lim} x^2+10x+25[/latex]
  3. [latex]\underset{x\to \infty }{\lim}\dfrac{3x+2}{x+5}[/latex]

For the following exercises (23-28), draw a graph of the functions without using a calculator. Be sure to notice all important features of the graph: local maxima and minima, inflection points, and asymptotic behavior.

  1. [latex]y=x^3-3x^2+4[/latex]
  2. [latex]y=\dfrac{x^3+4x^2+3x}{3x+9}[/latex]
  3. [latex]y=\sqrt{x^2-5x+4}[/latex]
  4. [latex]y=\dfrac{ \cos x}{x}[/latex], on [latex]x=[-2\pi ,2\pi][/latex]
  5. [latex]y=x \tan x, \, x=[−\pi ,\pi][/latex]
  6. [latex]y=x^2 \sin (x), \, x=[-2\pi ,2\pi][/latex]

Applied Optimization Problems

For the following exercises (1-4), answer by proof, counterexample, or explanation.

  1. When you find the maximum for an optimization problem, why do you need to check the sign of the derivative around the critical points?
  2. Why do you need to check the endpoints for optimization problems?
  3. True or False. For every continuous nonlinear function, you can find the value [latex]x[/latex] that maximizes the function.
  4. True or False. For every continuous nonconstant function on a closed, finite domain, there exists at least one [latex]x[/latex] that minimizes or maximizes the function.

For the following exercises (5-6), set up and evaluate each optimization problem.

  1. To carry a suitcase on an airplane, the length + width + height of the box must be less than or equal to [latex]62[/latex] in. Assuming the height is fixed, show that the maximum volume is [latex]V=h(31-(\frac{1}{2})h)^2[/latex]. What height allows you to have the largest volume?
  2. Find the positive integer that minimizes the sum of the number and its reciprocal.

For the following exercises (7-9), consider the construction of a pen to enclose an area.

  1. You have [latex]400[/latex] ft of fencing to construct a rectangular pen for cattle. What are the dimensions of the pen that maximize the area?
  2. You need to construct a fence around an area of [latex]1600[/latex] ft. What are the dimensions of the rectangular pen to minimize the amount of material needed?
  3. You are moving into a new apartment and notice there is a corner where the hallway narrows from [latex]8[/latex] ft to [latex]6[/latex] ft. What is the length of the longest item that can be carried horizontally around the corner? An upside L-shaped figure is drawn with the _ part being 6 wide and the | part being 8 wide. There is a line drawn from the _ part to the | part that touches the near corner of the shape to form a hypotenuse for a right triangle the other sides being the the rest of the _ and | parts. This line is marked L.

For the following problems (10-11), consider a lifeguard at a circular pool with diameter [latex]40[/latex] m. He must reach someone who is drowning on the exact opposite side of the pool, at position [latex]C[/latex]. The lifeguard swims with a speed [latex]v[/latex] and runs around the pool at speed [latex]w=3v[/latex].

A circle is drawn with points A and C on a diameter. There is a point B drawn on the circle such that angle BAC form an acute angle θ.

  1. Find a function that measures the total amount of time it takes to reach the drowning person as a function of the swim angle, [latex]\theta[/latex].
  2. Find at what angle [latex]\theta[/latex] the lifeguard should swim to reach the drowning person in the least amount of time.

For the following exercises (12-13), consider a limousine that gets [latex]m(v)=\frac{(120-2v)}{5}[/latex] mi/gal at speed [latex]v[/latex], the chauffeur costs [latex]$15[/latex]/h, and gas is [latex]$3.50[/latex]/gal.

  1. Find the cost per mile at speed [latex]v[/latex].
  2. Find the cheapest driving speed.

For the following exercises (14-15), consider a pizzeria that sell pizzas for a revenue of [latex]R(x)=ax[/latex] and costs [latex]C(x)=b+cx+dx^2[/latex], where [latex]x[/latex] represents the number of pizzas.

  1. Find the profit function for the number of pizzas. How many pizzas gives the largest profit per pizza?
  2. Assume that [latex]R(x)=10x[/latex] and [latex]C(x)=2x+x^2[/latex]. How many pizzas sold maximizes the profit?

For the following exercises (16-17), consider a wire 4 ft long cut into two pieces. One piece forms a circle with radius [latex]r[/latex] and the other forms a square of side [latex]x[/latex].

  1. Choose [latex]x[/latex] to maximize the sum of their areas.
  2. Choose [latex]x[/latex] to minimize the sum of their areas.

For the following exercises (18-19), consider two nonnegative numbers [latex]x[/latex] and [latex]y[/latex] such that [latex]x+y=10[/latex]. Maximize and minimize the quantities.

  1. [latex]xy[/latex]
  2. [latex]y-\frac{1}{x}[/latex]

For the following exercises (20-22), draw the given optimization problem and solve.

  1. Find the volume of the largest right circular cylinder that fits in a sphere of radius [latex]1[/latex].
  2. Find the area of the largest rectangle that fits into the triangle with sides [latex]x=0, \, y=0[/latex] and [latex]\frac{x}{4}+\frac{y}{6}=1[/latex].
  3. Find the dimensions of the closed cylinder volume [latex]V=16\pi[/latex] that has the least amount of surface area.

For the following exercises (23-24), consider the points on the given graphs. Use a calculator to graph the functions.

  1. Where is the line [latex]y=5-2x[/latex] closest to the origin?
  2. Where is the parabola [latex]y=x^2[/latex] closest to point [latex](2,0)[/latex]?

For the following exercises (25-27), set up, but do not evaluate, each optimization problem.

  1. A window is composed of a semicircle placed on top of a rectangle. If you have [latex]20[/latex] ft of window-framing materials for the outer frame, what is the maximum size of the window you can create? Use [latex]r[/latex] to represent the radius of the semicircle.

    A semicircular window is drawn with radius r.

  2. You are constructing a box for your cat to sleep in. The plush material for the square bottom of the box costs [latex]$5 / \text{ft}^2[/latex] and the material for the sides costs [latex]$2 / \text{ft}^2[/latex]. You need a box with volume [latex]4 \, \text{ft}^2[/latex]. Find the dimensions of the box that minimize cost. Use [latex]x[/latex] to represent the length of the side of the box.
  3. You are the manager of an apartment complex with [latex]50[/latex] units. When you set rent at [latex]$800[/latex]/month, all apartments are rented. As you increase rent by [latex]$25[/latex]/month, one fewer apartment is rented. Maintenance costs run [latex]$50[/latex]/month for each occupied unit. What is the rent that maximizes the total amount of profit?

L’Hôpital’s Rule

For the following exercises (1-3), evaluate the limit.

  1. Evaluate the limit [latex]\underset{x\to \infty }{\lim}\frac{e^x}{x^k}[/latex].
  2. Evaluate the limit [latex]\underset{x\to a}{\lim}\frac{x-a}{x^2-a^2}, \,\ a\ne 0[/latex].
  3. Evaluate the limit [latex]\underset{x\to a}{\lim}\frac{x-a}{x^n-a^n}, \,\ a\ne 0[/latex].

For the following exercises (4-5), determine whether you can apply L’Hôpital’s rule directly. Explain why or why not. Then, indicate if there is some way you can alter the limit so you can apply L’Hôpital’s rule.

  1. [latex]\underset{x\to \infty }{\lim} x^{1/x}[/latex]
  2. [latex]\underset{x\to 0}{\lim}\frac{x^2}{1/x}[/latex]

For the following exercises (6-20), evaluate the limits with either L’Hôpital’s rule or previously learned methods.

  1. [latex]\underset{x\to 3}{\lim}\frac{x^2-9}{x-3}[/latex]
  2. [latex]\underset{x\to 0}{\lim}\frac{(1+x)^{-2}-1}{x}[/latex]
  3. [latex]\underset{x\to \pi }{\lim}\frac{x-\pi }{\sin x}[/latex]
  4. [latex]\underset{x\to 0}{\lim}\frac{(1+x)^n-1}{x}[/latex]
  5. [latex]\underset{x\to 0}{\lim}\frac{\sin x- \tan x}{x^3}[/latex]
  6. [latex]\underset{x\to 0}{\lim}\frac{e^x-x-1}{x^2}[/latex]
  7. [latex]\underset{x\to 1}{\lim}\frac{x-1}{\ln x}[/latex]
  8. [latex]\underset{x\to 1}{\lim}\frac{\sqrt{x}-\sqrt[3]{x}}{x-1}[/latex]
  9. [latex]\underset{x\to \infty }{\lim} x \sin (\frac{1}{x})[/latex]
  10. [latex]\underset{x\to 0^+}{\lim} x \ln (x^4)[/latex]
  11. [latex]\underset{x\to \infty }{\lim} x^2 e^{−x}[/latex]
  12. [latex]\underset{x\to 0}{\lim}\frac{1+1/x}{1-1/x}[/latex]
  13. [latex]\underset{x\to \infty }{\lim} xe^{1/x}[/latex]
  14. [latex]\underset{x\to 0^{+}}{\lim} x^{1/x}[/latex]
  15. [latex]\underset{x\to \infty }{\lim} (1-\frac{1}{x})^x[/latex]

For the following exercises (21-25), use a calculator to graph the function and estimate the value of the limit, then use L’Hôpital’s rule to find the limit directly.

  1. [latex]\underset{x\to 0}{\lim}x \sin (\frac{1}{x})[/latex]
  2. [latex]\underset{x\to 1}{\lim}\frac{e^{x-1}-1}{x-1}[/latex]
  3. [latex]\underset{x\to \pi }{\lim}\frac{1+ \cos x}{ \sin x}[/latex]
  4. [latex]\underset{x\to 0^+}{\lim} \tan (x^x)[/latex]
  5. [latex]\underset{x\to 0}{\lim}\frac{e^x-e^{−x}}{x}[/latex]

Newton’s Method

For the following exercises (1-2), write Newton’s formula as [latex]x_{n+1}=F(x_n)[/latex] for solving [latex]f(x)=0[/latex].

  1. [latex]f(x)=x^3+2x+1[/latex]
  2. [latex]f(x)=e^x[/latex]

For the following exercises (3-4), solve [latex]f(x)=0[/latex] using the iteration [latex]x_{n+1}=x_n-cf(x_n)[/latex], which differs slightly from Newton’s method. Find a [latex]c[/latex] that works and a [latex]c[/latex] that fails to converge, with the exception of [latex]c=0[/latex].

  1. [latex]f(x)=x^2-4[/latex], with [latex]x_0=0[/latex]
  2. What is the value of “[latex]c[/latex]” for Newton’s method?

For the following exercises (5-8), start at [latex]x_0=0.6[/latex] and [latex]x_0=2[/latex]. Compute [latex]x_1[/latex] and [latex]x_2[/latex] using the specified iterative method.

  1. [latex]x_{n+1}=2x_n(1-x_n)[/latex]
  2. [latex]x_{n+1}=\frac{1}{\sqrt{x_n}}[/latex]
  3. [latex]x_{n+1}=(x_n)^2+x_n-2[/latex]
  4. [latex]x_{n+1}=|x_n|[/latex]

For the following exercises (9-13), solve to four decimal places using Newton’s method and a computer or calculator. Choose any initial guess [latex]x_0[/latex] that is not the exact root.

  1. [latex]x^4-100=0[/latex]
  2. [latex]x^3-x=0[/latex]
  3. [latex]x+ \tan (x)=0[/latex], choose [latex]x_0 \in (-\frac{\pi}{2},\frac{\pi }{2})[/latex]
  4. [latex]1+x+x^2+x^3+x^4=2[/latex]
  5. [latex]x= \sin^2 (x)[/latex]

For the following exercises (14-16), use Newton’s method to find the fixed points of the function where [latex]f(x)=x[/latex]; round to three decimals.

  1. [latex]\tan (x)[/latex] on [latex]x \in (\frac{\pi }{2},\frac{3\pi }{2})[/latex]
  2. [latex]\ln (x)+2[/latex]

Newton’s method can be used to find maxima and minima of functions in addition to the roots. In this case apply Newton’s method to the derivative function [latex]f^{\prime}(x)[/latex] to find its roots, instead of the original function. For the following exercises (16-17), consider the formulation of the method.

  1. To find candidates for maxima and minima, we need to find the critical points [latex]f^{\prime}(x)=0[/latex]. Show that to solve for the critical points of a function [latex]f(x)[/latex], Newton’s method is given by [latex]x_{n+1}=x_n-\frac{f^{\prime}(x_n)}{f^{\prime \prime}(x_n)}[/latex].

  2. What additional restrictions are necessary on the function [latex]f[/latex]?

For the following exercises (18-21), use Newton’s method to find the location of the local minima and/or maxima of the following functions; round to three decimals.

  1. Minimum of [latex]f(x)=3x^3+2x^2-16[/latex]
  2. Maximum of [latex]f(x)=x+\frac{1}{x}[/latex]
  3. Maximum of [latex]f(x)=\frac{\sqrt{x}-\sqrt[3]{x}}{x}[/latex]
  4. Minimum of [latex]f(x)=x^4+x^3+3x^2+12x+6[/latex]

For the following exercises (22-23), use the specified method to solve the equation. If it does not work, explain why it does not work.

  1. Newton’s method, [latex]0=e^x[/latex]
  2. Solving [latex]x_{n+1}=−(x_n)^3[/latex] starting at [latex]x_0=-1[/latex]

For the following exercises (24-25), use the secant method, an alternative iterative method to Newton’s method. The formula is given by

[latex]x_n=x_{n-1}-f(x_{n-1})\frac{x_{n-1}-x_{n-2}}{f(x_{n-1})-f(x_{n-2})}[/latex].
  1. Find a root to [latex]0= \sin x+3x[/latex] accurate to four decimal places.
  2. Find a root to [latex]\ln (x+2)=\frac{1}{2}[/latex] accurate to four decimal places.

For the following exercises (26-28), use both Newton’s method and the secant method to calculate a root for the following equations. Use a calculator or computer to calculate how many iterations of each are needed to reach within three decimal places of the exact answer. For the secant method, use the first guess from Newton’s method.

  1. [latex]f(x)=x^2+2x+1, \, x_0=1[/latex]
  2. [latex]f(x)= \sin x, \, x_0=1[/latex]
  3. [latex]f(x)=x^3+2x+4, \, x_0=0[/latex]

In the following exercise, consider Kepler’s equation regarding planetary orbits, [latex]M=E-\varepsilon \sin (E)[/latex], where [latex]M[/latex] is the mean anomaly, [latex]E[/latex] is eccentric anomaly, and [latex]\varepsilon[/latex] measures eccentricity.

  1. Use Newton’s method to solve for the eccentric anomaly [latex]E[/latex] when the mean anomaly [latex]M=\frac{3\pi }{2}[/latex] and the eccentricity of the orbit [latex]\varepsilon =0.8[/latex]; round to three decimals.

The following exercise involves a bank investment. The initial investment is [latex]$10,000[/latex]. After 25 years, the investment has tripled to [latex]$30,000[/latex].

  1. Use Newton’s method to determine the interest rate if the interest was compounded continuously.

Antiderivatives

For the following exercises (1-3), show that [latex]F(x)[/latex] is an antiderivative of [latex]f(x)[/latex].

  1. [latex]F(x)=5x^3+2x^2+3x+1, \, f(x)=15x^2+4x+3[/latex]
  2. [latex]F(x)=x^2e^x, \, f(x)=e^x(x^2+2x)[/latex]
  3. [latex]F(x)=e^x, \, f(x)=e^x[/latex]

For the following exercises (4-5), find the antiderivative of the function.

  1. [latex]f(x)=e^x-3x^2+ \sin x[/latex]
  2. [latex]f(x)=x-1+4 \sin (2x)[/latex]

For the following exercises (6-13), find the antiderivative [latex]F(x)[/latex] of each function [latex]f(x)[/latex].

  1. [latex]f(x)=x+12x^2[/latex]
  2. [latex]f(x)=(\sqrt{x})^3[/latex]
  3. [latex]f(x)=\dfrac{x^{1/3}}{x^{2/3}}[/latex]
  4. [latex]f(x)=\sec^2 (x)+1[/latex]
  5. [latex]f(x)= \sin^2 (x) \cos (x)[/latex]
  6. [latex]f(x)=\frac{1}{2} \csc^2 (x)+\frac{1}{x^2}[/latex]
  7. [latex]f(x)=4 \csc x \cot x- \sec x \tan x[/latex]
  8. [latex]f(x)=\frac{1}{2}e^{-4x}+ \sin x[/latex]

For the following exercises (14-17), evaluate the integral.

  1. [latex]\displaystyle\int \sin x dx[/latex]
  2. [latex]\displaystyle\int \frac{3x^2+2}{x^2} dx[/latex]
  3. [latex]\displaystyle\int (4\sqrt{x}+\sqrt[4]{x}) dx[/latex]
  4. [latex]\displaystyle\int \frac{14x^3+2x+1}{x^3} dx[/latex]

For the following exercises (18-20), solve the initial value problem.

  1. [latex]f^{\prime}(x)=x^{-3}, \, f(1)=1[/latex]
  2. [latex]f^{\prime}(x)= \cos x+ \sec^2 (x), \, f(\frac{\pi}{4})=2+\frac{\sqrt{2}}{2}[/latex]
  3. [latex]f^{\prime}(x)=\frac{2}{x^2}-\frac{x^2}{2}, \, f(1)=0[/latex]

For the following exercises (21-22), find two possible functions [latex]f[/latex] given the second- or third-order derivatives.

  1. [latex]f^{\prime \prime}(x)=e^{−x}[/latex]
  2. [latex]f^{\prime \prime \prime}(x)= \cos x[/latex]

For the following exercises (23-27), solve each problem.

  1. A car is being driven at a rate of [latex]40[/latex] mph when the brakes are applied. The car decelerates at a constant rate of [latex]10[/latex] ft/sec2. How long before the car stops?
  2. In the preceding problem, calculate how far the car travels in the time it takes to stop.
  3. You are merging onto the freeway, accelerating at a constant rate of [latex]12[/latex] ft/sec2. How long does it take you to reach merging speed at [latex]60[/latex] mph?
  4. Based on the previous problem, how far does the car travel to reach merging speed?
  5. A car company wants to ensure its newest model can stop in [latex]8[/latex] sec when traveling at [latex]75[/latex] mph. If we assume constant deceleration, find the value of deceleration that accomplishes this.

For the following exercises(28-30), find the antiderivative of the function, assuming [latex]F(0)=0[/latex].

  1. [latex]f(x)=x^2+2[/latex]
  2. [latex]f(x)= \sin x+2x[/latex]
  3. [latex]f(x)=\dfrac{1}{(x+1)^2}[/latex]

For the following exercises (31-32), determine whether the statement is true or false. Either prove it is true or find a counterexample if it is false.

  1. If [latex]f(x)[/latex] is the antiderivative of [latex]v(x)[/latex], then [latex]2f(x)[/latex] is the antiderivative of [latex]2v(x)[/latex].
  2. If [latex]f(x)[/latex] is the antiderivative of [latex]v(x)[/latex], then [latex]f(x)+1[/latex] is the antiderivative of [latex]v(x)+1[/latex].