Contextual Applications of Derivatives: Background You’ll Need 1

Lumen Learning

Contextual Applications of Derivatives: Background You’ll Need 1

Change logarithmic equations into exponential equations

Convert from Logarithmic to Exponential Form

Understanding the relationship between logarithmic and exponential forms is fundamental. This conversion can be succinctly represented as follows:

${\mathrm{log}}_{b}\left(x\right)=y\Leftrightarrow {b}^{y}=x,\text{}b>0,b\ne 1$

Here, $b$ is always a positive number and cannot be equal to $1$ .

Think b to the y equals x.

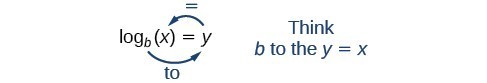
The logarithm function $\log_{b}(x)$ is conventionally written with parentheses to clearly denote the function’s input, similar to $f(x)$ . However, when dealing with a single variable or a simple expression, parentheses might be omitted, leading to the notation $\log_{b}x$ . It’s important to note that many calculators might still require parentheses around the input $x$ .

The notation $\log_{b}(c)=a$ can be interpreted as $b^a=c$ . This implies that the base $b$ raised to the power $a$ equals $c$ .

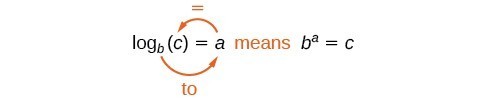
logb (c) = a means b to the A power equals C.

It’s common to see $ln$ representing the natural logarithm, which uses $e$ (approximately $2.718$ ) as its base. The notation $ln$ corresponds to $\log_e$ , emphasizing the natural logarithm’s specific base.

logarithmic functions

A logarithm base $b$ of a positive number $x$ satisfies the following definition: For $x>0,b>0,b\ne 1$ , $y={\mathrm{log}}_{b}\left(x\right)\text{ is equal to }{b}^{y}=x$ , where

we read ${\mathrm{log}}_{b}\left(x\right)$ as, “the logarithm with base $b$ of $x$ ” or the “log base $b$ of $x$ .”
the logarithm y is the exponent to which $b$ must be raised to get $x$ .
if no base $b$ is indicated, the base of the logarithm is assumed to be $10$ .

Also, since the logarithmic and exponential functions switch the $x$ and $y$ values, the domain and range of the exponential function are interchanged for the logarithmic function. Therefore,

the domain of the logarithm function with base $b \text{ is} \left(0,\infty \right)$ .
the range of the logarithm function with base $b \text{ is} \left(-\infty ,\infty \right)$ .

Can we take the logarithm of a negative number?

No. Because the base of an exponential function is always positive, no power of that base can ever be negative. We can never take the logarithm of a negative number. Also, we cannot take the logarithm of zero. Calculators may output a log of a negative number when in complex mode, but the log of a negative number is not a real number.

How To: Convert a Logarithmic Equation to Exponential Form

Given a logarithmic equation in the format $\log_{b}(x)=y$ :

Identify the Components: Recognize $b$ as the base, $y$ as the logarithmic result, and $x$ as the argument of the logarithm.
Convert to Exponential Form: Rewrite the equation from logarithmic to exponential form by setting the base $b$ raised to the power $y$ equal to $x$ . This translates to $b^y=x$ .

Write the following logarithmic equations in exponential form.

${\mathrm{log}}_{6}\left(\sqrt{6}\right)=\frac{1}{2}$
${\mathrm{log}}_{3}\left(9\right)=2$
${\mathrm{log}}_{10}\left(1,000,000\right)=6$
${\mathrm{log}}_{5}\left(25\right)=2$

First, identify the values of

b

$b$ ,

y

$y$ , and

x

$x$ . Then, write the equation in the form

b^{y} = x

${b}^{y}=x$ .

${\mathrm{log}}_{6}\left(\sqrt{6}\right)=\frac{1}{2}$ Here, $b=6,y=\frac{1}{2},\text{and } x=\sqrt{6}$ . Therefore, the equation ${\mathrm{log}}_{6}\left(\sqrt{6}\right)=\frac{1}{2}$ is equal to ${6}^{\frac{1}{2}}=\sqrt{6}$ .
${\mathrm{log}}_{3}\left(9\right)=2$ Here, $b = 3$ , $y = 2$ , and $x = 9$ . Therefore, the equation ${\mathrm{log}}_{3}\left(9\right)=2$ is equal to ${3}^{2}=9$ .
${\mathrm{log}}_{10}\left(1,000,000\right)=6$ is equal to ${10}^{6}=1,000,000$
${\mathrm{log}}_{5}\left(25\right)=2$ is equal to ${5}^{2}=25$

Convert from Exponential to Logarithmic Form

To convert from exponential to logarithmic form, we follow the same steps in reverse. We identify the base $b$ , exponent $x$ , and output $y$ . Then we write $x={\mathrm{log}}_{b}\left(y\right)$ .

Write the following exponential equations in logarithmic form.

${2}^{3}=8$
${5}^{2}=25$
${10}^{-4}=\frac{1}{10,000}$

First, identify the values of

b

$b$ ,

y

$y$ , and

x

$x$ . Then, write the equation in the form

x = {l o g}_{b} (y)

$x={\mathrm{log}}_{b}\left(y\right)$ .

${2}^{3}=8$ Here, $b = 2$ , $x = 3$ , and $y = 8$ . Therefore, the equation ${2}^{3}=8$ is equal to ${\mathrm{log}}_{2}\left(8\right)=3$ .
${5}^{2}=25$ Here, $b = 5$ , $x = 2$ , and $y = 25$ . Therefore, the equation ${5}^{2}=25$ is equal to ${\mathrm{log}}_{5}\left(25\right)=2$ .
${10}^{-4}=\frac{1}{10,000}$ Here, $b = 10$ , $x = –4,$ and $y=\frac{1}{10,000}$ . Therefore, the equation ${10}^{-4}=\frac{1}{10,000}$ is equal to ${\text{log}}_{10}\left(\frac{1}{10,000}\right)=-4$ .