Calculus of the Hyperbolic Functions: Learn It 1

Lumen Learning

Calculus of the Hyperbolic Functions: Learn It 1

Differentiate and integrate hyperbolic functions and their inverse forms
Understand the practical situations where the catenary curve appears

Derivatives and Integrals of the Hyperbolic Functions

The hyperbolic sine ( $sinh$ ) and hyperbolic cosine ( $cosh$ ) functions are defined as:

sinh x = \frac{e^{x} - e^{- x}}{2} and cosh x = \frac{e^{x} + e^{- x}}{2}

$\text{sinh}x=\dfrac{{e}^{x}-{e}^{\text{−}x}}{2}\text{ and }\text{cosh}x=\dfrac{{e}^{x}+{e}^{\text{−}x}}{2}$

The other hyperbolic functions are then defined in terms of $\text{sinh}x$ and $\text{cosh}x.$ The graphs of these functions provide insights into their behaviors.

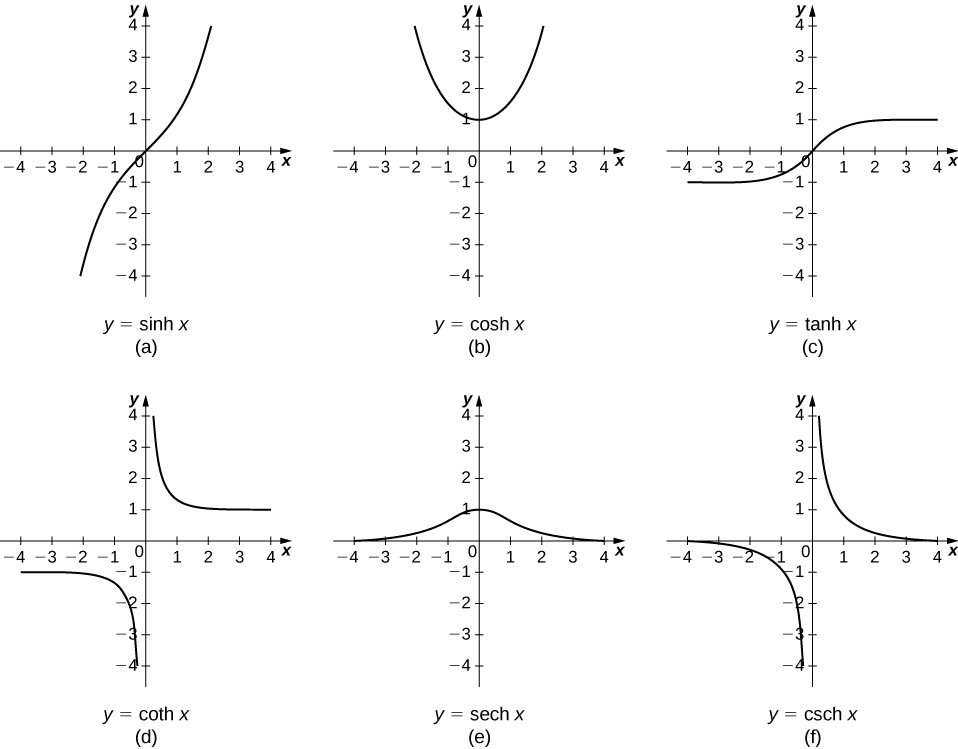
This figure has six graphs. The first graph labeled “a” is of the function y=sinh(x). It is an increasing function from the 3rd quadrant, through the origin to the first quadrant. The second graph is labeled “b” and is of the function y=cosh(x). It decreases in the second quadrant to the intercept y=1, then becomes an increasing function. The third graph labeled “c” is of the function y=tanh(x). It is an increasing function from the third quadrant, through the origin, to the first quadrant. The fourth graph is labeled “d” and is of the function y=coth(x). It has two pieces, one in the third quadrant and one in the first quadrant with a vertical asymptote at the y-axis. The fifth graph is labeled “e” and is of the function y=sech(x). It is a curve above the x-axis, increasing in the second quadrant, to the y-axis at y=1 and then decreases. The sixth graph is labeled “f” and is of the function y=csch(x). It has two pieces, one in the third quadrant and one in the first quadrant with a vertical asymptote at the y-axis. — Figure 1. Graphs of the hyperbolic functions.

It is straightforward to develop differentiation formulas for hyperbolic functions. For instance:

\begin{matrix} \frac{d}{d x} (sinh x) & = \frac{d}{d x} (\frac{e^{x} - e^{- x}}{2}) = \frac{1}{2} [\frac{d}{d x} (e^{x}) - \frac{d}{d x} (e^{- x})] = \frac{1}{2} [e^{x} + e^{- x}] = cosh x . \end{matrix}

$\begin{array}{cc}\hfill \frac{d}{dx}(\text{sinh}x)& =\frac{d}{dx}(\frac{{e}^{x}-{e}^{\text{−}x}}{2})\hfill \\ & =\frac{1}{2}\left[\frac{d}{dx}({e}^{x})-\frac{d}{dx}({e}^{\text{−}x})\right]\hfill \\ & =\frac{1}{2}\left[{e}^{x}+{e}^{\text{−}x}\right]=\text{cosh}x.\hfill \end{array}$

Similarly, $(\frac{d}{dx})\text{cosh}x=\text{sinh}x.$

derivatives of the hyperbolic functions

Derivatives of the Hyperbolic Functions
$f(x)$	$\frac{d}{dx}f(x)$
$\text{sinh}x$	$\text{cosh}x$
$\text{cosh}x$	$\text{sinh}x$
$\text{tanh}x$	${\text{sech}}^{2}x$
$\text{coth}x$	$\text{−}{\text{csch}}^{2}x$
$\text{sech}x$	$\text{−}\text{sech}x\text{tanh}x$
$\text{csch}x$	$\text{−}\text{csch}x\text{coth}x$

The derivatives of hyperbolic functions share similarities with those of trigonometric functions. For example:

$(\frac{d}{dx}) \sin x= \cos x$ and $(\frac{d}{dx})\text{sinh}x=\text{cosh}x.$

However, the derivatives of the cosine functions differ in sign:

$(\frac{d}{dx}) \cos x=\text{−} \sin x,$ but $(\frac{d}{dx})\text{cosh}x=\text{sinh}x.$

Using the differentiation formulas, we can derive the integral formulas for hyperbolic functions.

integral formulas for hyperbolic functions

$\begin{array}{cccccccc}\hfill \displaystyle\int \text{sinh}udu& =\hfill & \text{cosh}u+C\hfill & & & \hfill \displaystyle\int {\text{csch}}^{2}udu& =\hfill & \text{−}\text{coth}u+C\hfill \\ \hfill \displaystyle\int \text{cosh}udu& =\hfill & \text{sinh}u+C\hfill & & & \hfill \displaystyle\int \text{sech}u\text{tanh}udu& =\hfill & \text{−}\text{sech}u+C\hfill \\ \hfill \displaystyle\int {\text{sech}}^{2}udu& =\hfill & \text{tanh}u+C\hfill & & & \hfill \displaystyle\int \text{csch}u\text{coth}udu& =\hfill & \text{−}\text{csch}u+C\hfill \end{array}$

Evaluate the following derivatives:

$\frac{d}{dx}(\text{sinh}({x}^{2}))$
$\frac{d}{dx}{(\text{cosh}x)}^{2}$

Using the formulas in the table on derivatives of the hyperbolic functions and the chain rule, we get

$\frac{d}{dx}(\text{sinh}({x}^{2}))=\text{cosh}({x}^{2})·2x$
$\frac{d}{dx}{(\text{cosh}x)}^{2}=2\text{cosh}x\text{sinh}x$

Evaluate the following integrals:

$\displaystyle\int x\text{cosh}({x}^{2})dx$
$\displaystyle\int \text{tanh}xdx$

We can use $u$ -substitution in both cases.

Let $u={x}^{2}.$ Then, $du=2xdx$ and
$\displaystyle\int x\text{cosh}({x}^{2})dx=\displaystyle\int \frac{1}{2}\text{cosh}udu=\frac{1}{2}\text{sinh}u+C=\frac{1}{2}\text{sinh}({x}^{2})+C.$
Let $u=\text{cosh}x.$ Then, $du=\text{sinh}xdx$ and
$\displaystyle\int \text{tanh}xdx=\displaystyle\int \frac{\text{sinh}x}{\text{cosh}x}dx=\displaystyle\int \frac{1}{u}du=\text{ln}|u|+C=\text{ln}|\text{cosh}x|+C.$

Note that $\text{cosh}x>0$ for all $x,$ so we can eliminate the absolute value signs and obtain

$\displaystyle\int \text{tanh}xdx=\text{ln}(\text{cosh}x)+C.$