Graphs of Polynomial Functions Basics
Knowing the degree of a polynomial function is useful in helping us predict what its graph will look like. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as [latex]x[/latex] gets very large or very small, so its behavior will dominate the graph.
For any polynomial, the graph of the polynomial will match the end behavior of the term of highest degree.
There are two other important features of polynomials that influence the shape of its graph. The first is whether the degree is even or odd, and the second is whether the leading term is negative.
Even Degree Polynomials
In the figure below, we show the graphs of [latex]f\left(x\right)={x}^{2},g\left(x\right)={x}^{4}[/latex], and [latex]h\left(x\right)={x}^{6}[/latex] which all have even degrees. Notice that these graphs have similar shapes, very much like that of a quadratic function. However, as the power increases, the graphs flatten somewhat near the origin and become steeper away from the origin.

Odd Degree Polynomials
The next figure shows the graphs of [latex]f\left(x\right)={x}^{3},g\left(x\right)={x}^{5}[/latex], and [latex]h\left(x\right)={x}^{7}[/latex] which all have odd degrees.

Notice that one arm of the graph points down and the other points up. This is because when your input is negative, you will get a negative output if the degree is odd. The following table of values shows this.
| [latex]x[/latex] | [latex]f(x)=x^4[/latex] | [latex]h(x)=x^5[/latex] |
| [latex]-1[/latex] | [latex]1[/latex] | [latex]-1[/latex] |
| [latex]-2[/latex] | [latex]16[/latex] | [latex]-32[/latex] |
| [latex]-3[/latex] | [latex]81[/latex] | [latex]-243[/latex] |
Now you try it.
Identify whether each graph represents a polynomial function that has a degree that is even or odd.
-

Graph of a polynomial function -
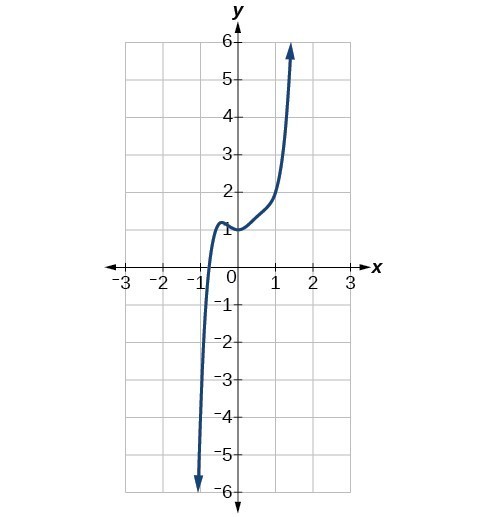
Graph of a polynomial function
The Sign of the Leading Term
What would happen if we change the sign of the leading term of an even degree polynomial? For example, let us say that the leading term of a polynomial is [latex]-3x^4[/latex]. We will use a table of values to compare the outputs for a polynomial with leading term [latex]-3x^4[/latex] and [latex]3x^4[/latex].
| [latex]x[/latex] | [latex]-3x^4[/latex] | [latex]3x^4[/latex] |
| [latex]-2[/latex] | [latex]-48[/latex] | [latex]48[/latex] |
| [latex]-1[/latex] | [latex]-3[/latex] | [latex]3[/latex] |
| [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] |
| [latex]1[/latex] | [latex]-3[/latex] | [latex]3[/latex] |
| [latex]2[/latex] | [latex]-48[/latex] | [latex]48[/latex] |
The grid below shows a plot with these points. The red points indicate a negative leading coefficient, and the blue points indicate a positive leading coefficient:
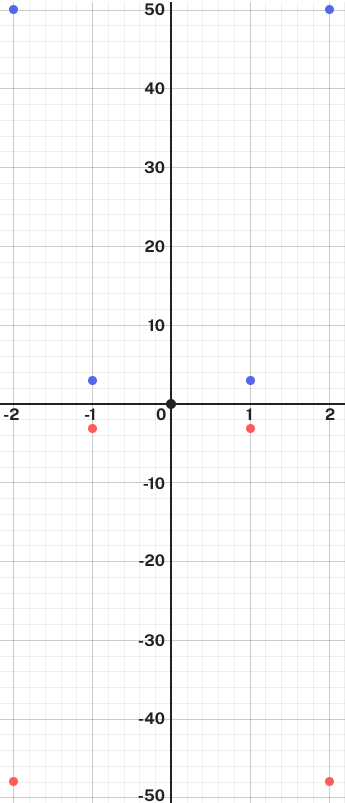
The negative sign creates a reflection of [latex]3x^4[/latex] across the [latex]x[/latex]-axis. The arms of a polynomial with a leading term of [latex]-3x^4[/latex] will point down, whereas the arms of a polynomial with leading term [latex]3x^4[/latex] will point up.
The table below summarizes all four cases mentioned.
Identify whether the leading term is positive or negative and whether the degree is even or odd for the following graphs of polynomial functions.
-

Graph of a polynomial function -
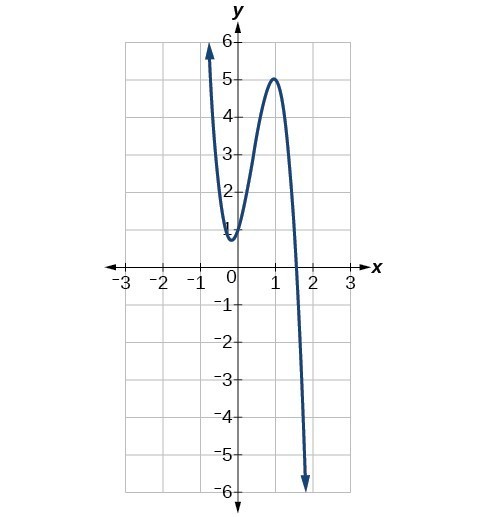
Graph of a polynomial function



