- Recognize the degree of a polynomial, find the roots of quadratic polynomials, and describe the graphs of basic odd and even polynomial functions
- Graph a piecewise-defined function
- Explain the difference between algebraic and transcendental functions
- Sketch the graph of a function that has been shifted, stretched, or reflected from its initial graph position
Polynomial Functions
The Main Idea
- A polynomial function is of the form [latex]f(x) = a₁xⁿ + a₂xⁿ⁻¹ + ... + aₙ₋₁x + aₙ,[/latex] where [latex]n[/latex] is a non-negative integer.
- Key Terms:
- Degree: The highest power of [latex]x[/latex] in the polynomial
- Leading Term: The term with the highest degree
- Leading Coefficient: The coefficient of the leading term
- Types of Polynomials:
- Linear: Degree [latex]1[/latex] (e.g., [latex]f(x) = mx + b[/latex])
- Quadratic: Degree [latex]2[/latex] (e.g., [latex]f(x) = ax² + bx + c[/latex])
- Cubic: Degree [latex]3[/latex]
- Higher degrees: Quartic ([latex]4[/latex]), Quintic ([latex]5[/latex]), etc.
- The zero function [latex]f(x) = 0[/latex] is considered a polynomial of degree [latex]0[/latex].
Identify the degree, leading term, and leading coefficient for each of the following functions:
- [latex]h(y) = 2y⁴ - 3y² + 5y - 7[/latex]
- [latex]k(s) = -0.5s³ + 2s - 1[/latex]
- [latex]m(w) = w⁵ + 3w⁴ - 2w² + w[/latex]
Zeros of Polynomial Functions
The Main Idea
- For quadratic functions [latex]f(x) = ax² + bx + c[/latex], zeros can be found using:
- Factoring (if possible)
- The quadratic formula: [latex]x = \dfrac{-b ± \sqrt{(b² - 4ac)}}{ (2a)}[/latex]
- The discriminant [latex](b² - 4ac)[/latex] determines the nature of quadratic solutions:
- Positive: Two distinct real roots
- Zero: One real root (double root)
- Negative: No real roots
- Higher-degree polynomials may have more complex methods for finding zeros.
Find the zeros of the quadratic function [latex]g(x) = 2x² + 5x - 3[/latex].
Graphs of Polynomial Functions Basics
The Main Idea
- The degree of a polynomial greatly influences its graph’s shape.
- Even-degree polynomials:
- Both ends of the graph point in the same direction (up or down)
- Similar to a parabola, but may be flatter near the origin
- Odd-degree polynomials:
- Ends of the graph point in opposite directions
- One end goes up, the other goes down
- The sign of the leading coefficient determines the direction of the graph’s ends:
- Positive leading coefficient: right end goes up
- Negative leading coefficient: right end goes down
- As the degree increases, graphs tend to flatten near the origin and become steeper away from it.
Describe the end behavior and basic shape of the graph for the polynomial function:
[latex]f(x) = -2x⁵ + 3x⁴ - x² + 7[/latex]
Piecewise-Defined Functions
The Main Idea
- A piecewise-defined function uses different formulas for different parts of its domain.
- Each piece of the function has its own subdomain, which together form the function’s complete domain.
- Piecewise functions may be continuous or discontinuous, depending on how the pieces connect.
- Each piece is graphed separately within its specified domain, paying special attention to the transition points.
Sketch a graph of the function
[latex]f(x)=\begin{cases} 2-x, & x \le 2 \\ x+2, & x>2 \end{cases}[/latex]
The cost of mailing a letter is a function of the weight of the letter. Suppose the cost of mailing a letter is [latex]49\text{¢}[/latex] for the first ounce and [latex]21\text{¢}[/latex] for each additional ounce. Write a piecewise-defined function describing the cost [latex]C[/latex] as a function of the weight [latex]x[/latex] for [latex]0 < x \le 3[/latex], where [latex]C[/latex] is measured in cents and [latex]x[/latex] is measured in ounces.
Algebraic Functions and Transcendental Functions
The Main Idea
- Algebraic Functions:
- Involve addition, subtraction, multiplication, division, rational powers, and roots
- Include polynomial, rational, and root functions
- Examples: [latex]f(x) = x³ + 2x - 1, g(x) = \frac{(x² + 1) }{ (x - 2)}, h(x) = \sqrt{(x + 3)}[/latex]
- Transcendental Functions:
- Cannot be expressed using a finite number of algebraic operations
- Main types: trigonometric, exponential, and logarithmic functions
- Examples: [latex]sin(x), e^x, log₂(x)[/latex]
Is [latex]f(x)=\dfrac{x}{2}[/latex] an algebraic or a transcendental function?
Classify the following functions as algebraic or transcendental, and identify their specific type if possible:
- [latex]f(x) = \frac{(x⁴ + 2x² - 5)}{ (x - 1)}[/latex]
- [latex]g(x) = sin(x²) + cos(x)[/latex]
- [latex]h(x) = \sqrt[3]{(x² + 1)} + log₃(x)[/latex]
- [latex]k(x) = \frac{(2^x + 3^x)}{x}[/latex]
Transformations of Functions
The Main Idea
- Vertical Shift: [latex]f(x) ± c[/latex]
- [latex]+c[/latex] shifts up, [latex]-c[/latex] shifts down
- Does not change shape of graph
- Horizontal Shift: [latex]f(x ± c)[/latex]
- [latex]-c[/latex] shifts right, [latex]+c[/latex] shifts left
- Does not change shape of graph
- Vertical Scaling: [latex]cf(x)[/latex]
- [latex]|c| > 1[/latex] stretches vertically, [latex]0 < |c| < 1[/latex] compresses vertically
- Changes height of graph
- Horizontal Scaling: [latex]f(cx)[/latex]
- [latex]0 < |c| < 1[/latex]stretches horizontally, [latex]|c| > 1[/latex] compresses horizontally
- Changes width of graph
- Reflections:
- [latex]-f(x)[/latex] reflects over [latex]x[/latex]-axis
- [latex]f(-x)[/latex] reflects over [latex]y[/latex]-axis
- Multiple Transformations: [latex]y = cf(a(x + b)) + d[/latex]
- Apply in order: horizontal shift, horizontal scaling, vertical scaling, vertical shift
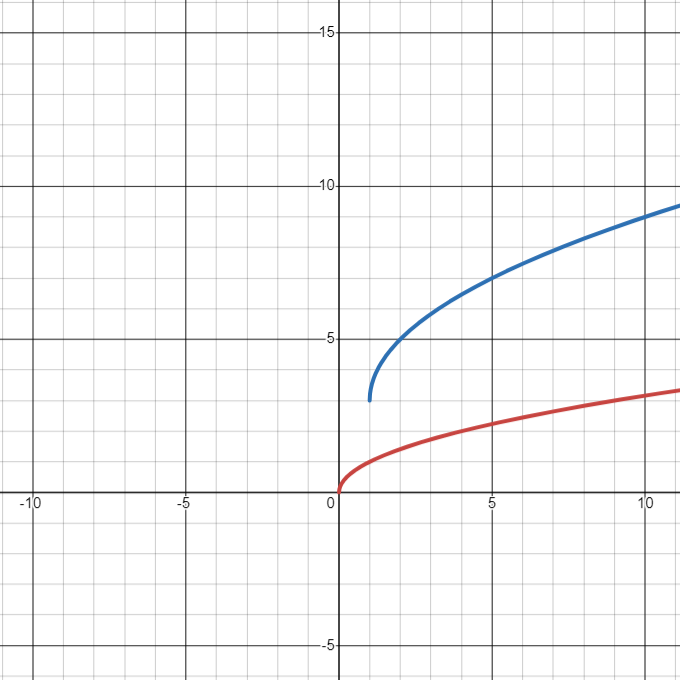
Transform the following function which has the base tool-kit function [latex]f(x) = \sqrt{x}[/latex]:
[latex]g(x) = 2\sqrt{(x - 1)} + 3[/latex]