Area of a Region between Two Curves

We have developed the concept of the definite integral to calculate the area below a curve on a given interval. Now, we will expand that idea to calculate the area of more complex regions.

Let [latex]f(x)[/latex] and [latex]g(x)[/latex] be continuous functions over an interval [latex]\left[a,b\right][/latex] such that [latex]f(x)\ge g(x)[/latex] on [latex]\left[a,b\right].[/latex] We want to find the area between the graphs of the functions.

As we did before, we are going to partition the interval on the [latex]x[/latex]-axis and approximate the area between the graphs of the functions with rectangles.

For [latex]i=0,1,2\text{,…},n,[/latex] let [latex]P=\left\{{x}_{i}\right\}[/latex] be a regular partition of [latex]\left[a,b\right].[/latex] Then, for [latex]i=1,2\text{,…},n,[/latex] choose a point [latex]{x}_{i}^{*}\in \left[{x}_{i-1},{x}_{i}\right],[/latex] and on each interval [latex]\left[{x}_{i-1},{x}_{i}\right][/latex] construct a rectangle that extends vertically from [latex]g({x}_{i}^{*})[/latex] to [latex]f({x}_{i}^{*}).[/latex].

The height of each individual rectangle is [latex]f({x}_{i}^{*})-g({x}_{i}^{*})[/latex] and the width of each rectangle is [latex]\text{Δ}x.[/latex] Adding the areas of all the rectangles, we see that the area between the curves is approximated by:

This is a Riemann sum, so we take the limit as [latex]n\to \infty[/latex] and we get:

These findings are summarized in the following theorem.

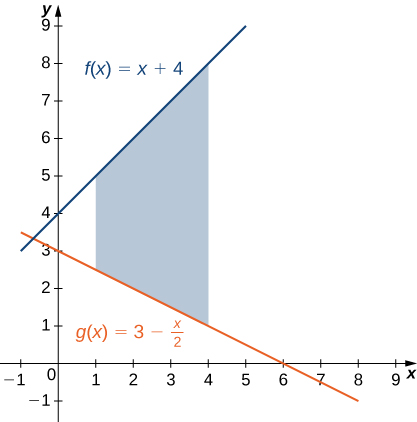
If [latex]R[/latex] is the region bounded above by the graph of the function [latex]f(x)=x+4[/latex] and below by the graph of the function [latex]g(x)=3-\frac{x}{2}[/latex] over the interval [latex]\left[1,4\right],[/latex] find the area of region [latex]R.[/latex]

Show Solution

The region is depicted in the following figure.

We have:

[latex]\begin{array}{cc}\hfill A& ={\displaystyle\int }_{a}^{b}\left[f(x)-g(x)\right]dx\hfill \\ & ={\displaystyle\int }_{1}^{4}\left[(x+4)-(3-\frac{x}{2})\right]dx={\displaystyle\int }_{1}^{4}\left[\frac{3x}{2}+1\right]dx\hfill \\ & ={\left[\frac{3{x}^{2}}{4}+x\right]|}_{1}^{4}=(16-\frac{7}{4})=\frac{57}{4}.\hfill \end{array}[/latex]

The area of the region is [latex]\frac{57}{4}{\text{units}}^{2}.[/latex]

In the last example, we defined the interval of interest as part of the problem statement. Quite often, though, we want to define our interval of interest based on where the graphs of the two functions intersect. This is illustrated in the following example.

If [latex]R[/latex] is the region bounded above by the graph of the function [latex]f(x)=9-{(\frac{x}{2})}^{2}[/latex] and below by the graph of the function [latex]g(x)=6-x,[/latex] find the area of region [latex]R.[/latex]

Show Solution

The region is depicted in the following figure.

We first need to compute where the graphs of the functions intersect. Setting [latex]f(x)=g(x),[/latex] we get:

[latex]\begin{array}{ccc}\hfill f(x)& =\hfill & g(x)\hfill \\ \\ \hfill 9-{(\frac{x}{2})}^{2}& =\hfill & 6-x\hfill \\ \hfill 9-\frac{{x}^{2}}{4}& =\hfill & 6-x\hfill \\ \hfill 36-{x}^{2}& =\hfill & 24-4x\hfill \\ \hfill {x}^{2}-4x-12& =\hfill & 0\hfill \\ \hfill (x-6)(x+2)& =\hfill & 0.\hfill \end{array}[/latex]

The graphs of the functions intersect when [latex]x=6[/latex] or [latex]x=-2,[/latex] so we want to integrate from [latex]-2[/latex] to [latex]6[/latex].

Since [latex]f(x)\ge g(x)[/latex] for [latex]-2\le x\le 6,[/latex] we obtain:

[latex]\begin{array}{cc}\hfill A& ={\displaystyle\int }_{a}^{b}\left[f(x)-g(x)\right]dx\hfill \\ & ={\displaystyle\int }_{-2}^{6}\left[9-{(\frac{x}{2})}^{2}-(6-x)\right]dx={\displaystyle\int }_{-2}^{6}\left[3-\frac{{x}^{2}}{4}+x\right]dx\hfill \\ & ={\left[3x-\frac{{x}^{3}}{12}+\frac{{x}^{2}}{2}\right]|}_{-2}^{6}=\frac{64}{3}.\hfill \end{array}[/latex]

The area of the region is [latex]\frac{64}{3}[/latex] units².