Approximating Areas: Learn It 1

  • Estimate the area under a curve by adding up the areas of rectangles
  • Estimate the area under a curve using Riemann sums

Approximating Area

Archimedes used a process known as the method of exhaustion to calculate the area of various shapes. This involved using smaller and smaller shapes to approximate the area more accurately. We can use a similar method to approximate the area under a curve, [latex]f(x)[/latex], between [latex]a[/latex] and b. By dividing the area into smaller rectangles, we get closer approximations.

Let [latex]f(x)[/latex] be a continuous, nonnegative function defined on the closed interval [latex][a,b][/latex]. Our goal is to approximate the area [latex]A[/latex] bounded by [latex]f(x)[/latex] above, the [latex]x[/latex]-axis below, the line [latex]x=a[/latex] on the left, and the line [latex]x=b[/latex] on the right (Figure 1).

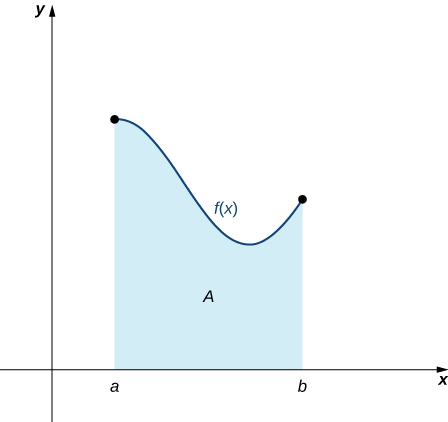
A graph in quadrant one of an area bounded by a generic curve f(x) at the top, the x-axis at the bottom, the line x = a to the left, and the line x = b to the right. About midway through, the concavity switches from concave down to concave up, and the function starts to increases shortly before the line x = b.
Figure 1. An area (shaded region) bounded by the curve [latex]f(x)[/latex] at top, the x-axis at bottom, the line [latex]x=a[/latex] to the left, and the line [latex]x=b[/latex] at right.

To approximate the area under this curve, we use a geometric approach. By dividing the region into many small shapes with known area formulas, we can sum these areas to estimate the true area reasonably well.

We begin by dividing the interval [latex][a,b][/latex] into [latex]n[/latex] subintervals of equal width, [latex]\frac{b-a}{n}[/latex]. We select equally spaced points [latex]x_0,x_1,x_2,\cdots,x_n[/latex] with [latex]x_0=a, \, x_n=b[/latex], and

[latex]x_i-x_{i-1}=\dfrac{b-a}{n}[/latex]

for [latex]i=1,2,3,\cdots,n[/latex].

The width of each subinterval is denoted as [latex]\Delta x[/latex], so [latex]\Delta x=\dfrac{b-a}{n}[/latex] and the points are defined by

[latex]x_i=x_0+i \Delta x[/latex]

for [latex]i=1,2,3,\cdots,n[/latex].

This method of dividing an interval [latex][a,b][/latex] into subintervals using equally spaced points is commonly used to approximate the area under a curve. Let’s define some relevant terminology to make this process clearer.

partition

A set of points [latex]P=\{x_i\}[/latex] for [latex]i=0,1,2,\cdots,n[/latex] with [latex]a=x_0 < x_1 < x_2 < \cdots < x_n=b[/latex], which divides the interval [latex][a,b][/latex] into subintervals of the form [latex][x_0,x_1], \, [x_1,x_2],\cdots,[x_{n-1},x_n][/latex] is called a partition of [latex][a,b][/latex]. If the subintervals all have the same width, the set of points forms a regular partition of the interval [latex][a,b][/latex].

We can use this regular partition as the basis of a method for estimating the area under the curve. We next examine two methods: the left-endpoint approximation and the right-endpoint approximation.

Left-Endpoint Approximation

On each subinterval [latex][x_{i-1},x_i][/latex] (for [latex]i=1,2,3,\cdots,n[/latex]), construct a rectangle with width [latex]\Delta x[/latex] and height equal to [latex]f(x_{i-1})[/latex], which is the function value at the left endpoint of the subinterval. Then the area of this rectangle is [latex]f(x_{i-1})\Delta x[/latex].

Adding the areas of all these rectangles, we get an approximate value for [latex]A[/latex]. We use the notation [latex]L_n[/latex] to denote that this is a left-endpoint approximation of [latex]A[/latex] using [latex]n[/latex] subintervals.

[latex]\begin{array}{ll} A \approx L_n & =f(x_0)\Delta x+f(x_1)\Delta x+\cdots+f(x_{n-1})\Delta x \\ & =\displaystyle\sum_{i=1}^{n} f(x_{i-1})\Delta x \end{array}[/latex]

left-endpoint approximation

In the left-endpoint approximation, we estimate the area under a curve by constructing rectangles whose heights are determined by the function values at the left endpoints of subintervals.
 
The approximation of the area [latex]A[/latex] using [latex]n[/latex] subintervals is given by the formula:
[latex]A \approx L_n = \displaystyle\sum_{i=1}^{n} f(x_{i-1})\Delta x[/latex]

where [latex]\Delta x =\frac{b-a}{n}[/latex] is the width of each subinterval, and [latex]x_{i-1}[/latex] are the left endpoints of the subintervals.

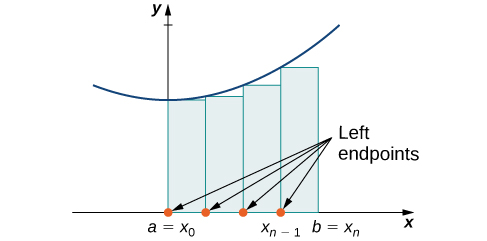
A diagram showing the left-endpoint approximation of area under a curve. Under a parabola with vertex on the y axis and above the x axis, rectangles are drawn between a=x0 on the origin and b = xn. The rectangles have endpoints at a=x0, x1, x2…x(n-1), and b = xn, spaced equally. The height of each rectangle is determined by the value of the given function at the left endpoint of the rectangle.
Figure 2. In the left-endpoint approximation of area under a curve, the height of each rectangle is determined by the function value at the left of each subinterval.

How to: Perform Left-Endpoint Approximation

  1. Identify the Interval and Function: Determine the interval [latex][a,b][/latex] and the function [latex]f(x)[/latex] you are working with.
  2. Divide the Interval: Divide [latex][a,b][/latex] into [latex]n[/latex] subintervals of equal width [latex]\Delta x =\frac{b-a}{n}[/latex].
  3. Determine Left Endpoints: Identify the left endpoints of each subinterval: [latex]x_0,x_1,x_2,\cdots,x_{n-1}[/latex]
  4. Evaluate the Function: Calculate the function values at each left endpoint: [latex]f(x_0), f(x_1), f(x_2), \cdots, f(x_{n-1})[/latex].
  5. Calculate Rectangle Areas: Multiply each function value by the width [latex]Δx[/latex] to get the area of each rectangle.
  6. Sum the Areas: Add up all the rectangle areas to get the approximate area under the curve
    [latex]A \approx \displaystyle\sum_{i=1}^{n} f(x_{i-1})\Delta x[/latex]