Applications of Integration: Get Stronger Answer Key

Areas Between Curves

  1. 323323
  2. 13121312
  3. 3636
  4. This figure is has two graphs. They are the functions f(x)=x^2 and g(x)=-x^2+18x. The region between the graphs is shaded, bounded above by g(x) and below by f(x). It is in the first quadrant.243243 square units
  5. This figure is has two graphs. They are the functions y=cos(x) and y=cos^2(x). The graphs are periodic and resemble waves. There are four regions created by intersections of the curves. The areas are shaded.44
  6. This figure is has two graphs. They are the functions f(x)=e^x and g(x)=e^-x. There are two shaded regions. In the second quadrant the region is bounded by x=-1, g(x) above and f(x) below. The second region is in the first quadrant and is bounded by f(x) above, g(x) below, and x=1.2(e−1)2e2(e−1)2e
  7. This figure is has two graphs. They are the functions f(x)=x^2 and g(x)=absolute value of x. There are two shaded regions. The first region is in the second quadrant and is between g(x) above and f(x) below. The second region is in the first quadrant and is bounded above by g(x) and below by f(x).1313
  8. This figure is has three graphs. They are the functions f(x)=squareroot of x, y=12-x, and y=1. The region between the graphs is shaded, bounded above and to the left by f(x), above and to the right by the line y=12-x, and below by the line y=1. It is in the first quadrant.343343
  9. This figure is has two graphs. They are the functions f(x)=x^3 and g(x)=x^2-2x. There are two shaded regions between the graphs. The first region is bounded to the left by the line x=-2, above by g(x) and below by f(x). The second region is bounded above by f(x), below by g(x) and to the right by the line x=2.5252
  10. This figure is has two graphs. They are the functions f(x)=x^3+3x and g(x)=4x. There are two shaded regions between the graphs. The first region is bounded above by f(x) and below by g(x). The second region is bounded above by g(x), below by f(x).1212
  11. This figure is has two graphs. They are the equations x=2y and x=y^3-y. The graphs intersect in the third quadrant and again in the first quadrant forming two closed regions in between them.9292
  12. This figure is has two graphs. They are the equations x=y+2 and y^2=x. The graphs intersect, forming a region in between them9292
  13. This figure is has two graphs. They are the equations x=cos(y) and x=sin(y). The graphs intersect, forming two regions bounded above by the line y=pi/2 and below by the line y=-pi/2.3√323√32
  14. This figure is has two graphs. They are the equations y=xe^x and y=e^x. The graphs intersect, forming a region in between them in the first quadrant.e−2e−2
  15. This figure is has two graphs. They are the equations x=-y^2+1 and x=y^3+2y^2. The graphs intersect, forming two regions in between them.274274
  16. This figure is has two graphs. They are the equations y=4-3x and y=1/x. The graphs intersect, having region between them shaded. The region is in the first quadrant.43−ln(3)43−ln(3)
  17. This figure is has two graphs. They are the equations y=x^2-3x+2 and y=x^3-2x^2-x+2. The graphs intersect, having region between them shaded.1212
  18. This figure is has two graphs. They are the equations 2y=x and y+y^3=x. The graphs intersect, forming two regions. The regions are shaded.1212
  19. This figure is has two graphs. They are the equations y=arccos(x) and y=arcsin (x). The graphs intersect, forming two regions. The first region is bounded to the left by x=-1. The second region is bounded to the right by x=1. Both regions are shaded.−2(√2−π)−2(√2−π)
  20. 1.0671.067
  21. 0.8520.852
  22. 7.5237.523
  23. 3π−412
  24. 1.429
  25. $33,333.33 total profit for 200 cell phones sold
  26. 3.263 mi represents how far ahead the hare is from the tortoise
  27. 34324
  28. 4√3
  29. π−3225

Determining Volumes by Slicing

  1.  
  2.  
  3.  
  4.  
  5.  
  6. 8 units3
  7. 323√2 units3
  8. 7π12hr2 units3
  9. This figure shows the x-axis and the y-axis with a line starting on the x-axis at (1,0) and ending on the y-axis at (0,1). Perpendicular to the xy-plane are 4 shaded semi-circles with their diameters beginning on the x-axis and ending on the line, decreasing in size away from the origin. π24 units3
  10. This figure shows the x-axis and the y-axis in 3-dimensional perspective. On the graph above the x-axis is a parabola, which has its vertex at y=1 and x-intercepts at (-1,0) and (1,0). There are 3 square shaded regions perpendicular to the x y plane, which touch the parabola on either side, decreasing in size away from the origin. 2 units3
  11. This figure is a graph with the x and y axes diagonal to show 3-dimensional perspective. On the first quadrant of the graph are the curves y=x, a line, and y=x^2, a parabola. They intersect at the origin and at (1,1). Several semicircular-shaped shaded regions are perpendicular to the x y plane, which go from the parabola to the line and perpendicular to the line. π240 units3
  12. This figure is a graph in the first quadrant. It is a shaded region bounded above by the curve y=2x^2, below by the x-axis, and to the right by the vertical line x=4. 4096π5 units3
  13. This figure is a graph in the first quadrant. It is a shaded region bounded above by the line y=1, below by the curve y=x^4, and to the left by the y-axis. 8π9 units3
  14. This figure is a shaded region bounded above by the curve y=cos(x), below to the left by the y-axis and below to the right by y=sin(x). The shaded region is in the first quadrant. π2 units3
  15. This figure is a graph in the first quadrant. It is a shaded region bounded above by the line x + y=9, below by the x-axis, to the left by the y-axis, and to the left by the curve x^2-y^2=9. 207π units3
  16. y=2x3,x=0,x=1, and y=0 This figure is a graph in the first quadrant. It is a shaded region bounded above by the curve y=2x^3, below by the x-axis, and to the right by the line x=1. 4π5 units3
  17. This figure is a graph in the first quadrant. It is a quarter of a circle with center at the origin and radius of 2. It is shaded on the inside. 16π3 units3
  18. This figure is a graph in the first quadrant. It is a shaded region bounded above by the line y=pi/4, to the right by the curve x=sec(y), below by the x-axis, and to the left by the y-axis. π units3
  19. This figure is a graph in the first quadrant. It is a shaded triangle bounded above by the line y=4-x, below by the line y=x, and to the left by the y-axis. 16π3 units3
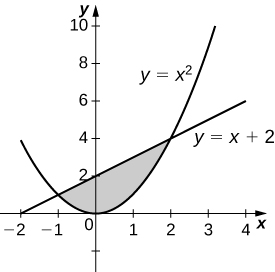  20. This figure is a graph above the x-axis. It is a shaded region bounded above by the line y=x+2, and below by the parabola y=x^2. 72π5 units3
  21. This figure is a shaded region bounded above by the curve y=4-x^2 and below by the line y=2-x. 108π5 units3
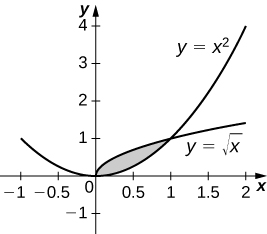  22. This figure is a graph in the first quadrant. It is a shaded region bounded above by the curve y=squareroot(x), below by the curve y=x^2. 3π10 units3
  23. This figure is a shaded region bounded above by the curve y=squareroot(4-x^2) and, below by the curve y=squareroot(1+x^2). 2√6π units3
  24. This figure is a graph in the first quadrant. It is a shaded region bounded above by the line y=x+2, below by the line y=2x-1, and to the left by the y-axis. 9π units3
  25. This figure is a graph in the first quadrant. It is a shaded region bounded above by the curve y=ln(2), below by the x-axis, to the left by the curve x=y^2, and to the right by the curve x=e^(2y). π20(75−4ln5(2)) units3
  26. m2π3(b3−a3) units3
  27. 4a2bπ3 units3
  28. 2π2 units3
  29. T2ab2π3 units3
  30. π12(r+h)2(6r−h) units3
  31. π3(h+R)(h−2R)2 units3

Volumes of Revolution: Cylindrical Shells

  1.  

This figure is a graph in the first quadrant. It is the line y=3x. Under the line and above the x-axis there is a shaded region. The region is bounded to the right at x=3.

    3

  1. This figure is a graph in the first quadrant. It is the line y=3x. Under the line and above the x-axis there is a shaded region. The region is bounded to the right at x=3. 81π units3
  2. This figure is a graph in the first quadrant. It is the increasing curve y=2x^3. Under the curve and above the x-axis there is a shaded region. The region is bounded to the right at x=2. 512π7 units3
  3. 2π units3
  4. 2π3 units3
  5. 2π units3
  6. 4π5 units3
  7. 64π3 units3
  8. 32π5 units3
  9. π(e−2) units3
  10. 28π3 units3
  11. −84π5 units3
  12. −eππ2 units3
  13. 64π5 units3
  14. 28π15 units3
  15. 3π10 units3
  16. 52π5 units3
  17. 0.9876 units3
  18. This figure is a graph. On the graph are two curves, y=cos(pi times x) and y=sin(pi times x). They are periodic curves resembling waves. The curves intersect in the first quadrant and also the fourth quadrant. The region between the two points of intersection is shaded. 3√2 units3
  19. This figure is a graph in the first quadrant. It is the parabola y=x^2-2x. . Under the curve and above the x-axis there is a shaded region. The region begins at x=2 and is bounded to the right at x=4. 496π15 units3
  20. This figure is a graph in the first quadrant. There are two curves on the graph. The first curve is y=3x^2-2 and the second curve is y=x. Between the curves there is a shaded region. The region begins at x=1 and is bounded to the right at x=2. 398π15 units3
  21. This figure is a graph. There are two curves on the graph. The first curve is x=y^2-2y+1 and is a parabola opening to the right. The second curve is x=y^2 and is a parabola opening to the right. Between the curves there is a shaded region. The shaded region is bounded to the right at x=2. 15.9074 units3
  22. 13πr2h units3
  23. πr2h units3

Arc Length of a Curve and Surface Area

  1. 2√26
  2. 2√17
  3. 13√13−827
  4. 43
  5. 2.0035
  6. 12332
  7. 10
  8. 203
  9. 1675(229√229−8)
  10. 18(4√5+ln(9+4√5))
  11. 1.201
  12. 15.2341
  13. 49π3
  14. 70π√2
  15. 8π
  16. 120π√26
  17. π6(17√17−1)
  18. 9√2π
  19. 10√10π27(73√73−1)
  20. 25.645
  21. 2π /li>
  22. 10.5017
  23. 23 ft
  24. 2
  25. Answers may vary
  26.