Applications of Integration: Get Stronger

Areas Between Curves

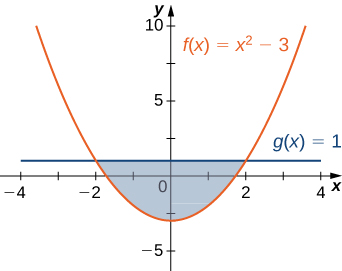
For the following exercise, determine the area of the region between the two curves in the given figure by integrating over the [latex]x\text{-axis}\text{.}[/latex]

  1. [latex]y={x}^{2}-3\text{ and }y=1[/latex]

    This figure is has two graphs. They are the functions f(x) = x^2-3and g(x)=1. In between these graphs is a shaded region, bounded above by g(x) and below by f(x). The shaded area is between x=-2 and x=2.

For the following exercise, split the region between the two curves into two smaller regions, then determine the area by integrating over the [latex]x\text{-axis}.[/latex] Note that you will have two integrals to solve.

  1. [latex]y={x}^{3}[/latex] and [latex]y={x}^{2}+x[/latex]

    This figure is has two graphs. They are the functions f(x) = x^3 and g(x)= x^2+x. These graphs intersect twice. The regions between the intersections are shaded. The first region is bounded above by f(x) and below by g(x). The second region is bounded above by g(x) and below by f(x).

For the following exercise, determine the area of the region between the two curves by integrating over the [latex]y\text{-axis}.[/latex]

  1. [latex]x={y}^{2}\text{ and }x=9[/latex]

    This figure is has two graphs. They are the equations x=y^2 and x=9. The region between the graphs is shaded. It is horizontal, between the y-axis and the line x=9.

For the following exercises (4-7), graph the equations and shade the area of the region between the curves. Determine its area by integrating over the [latex]x\text{-axis}.[/latex]

  1. [latex]y={x}^{2}\text{ and }y=\text{−}{x}^{2}+18x[/latex]
  2. [latex]y= \cos x[/latex] and [latex]y={ \cos }^{2}x[/latex] on [latex]x=\left[\text{−}\pi ,\pi \right][/latex]
  3. [latex]y={e}^{x},y={e}^{\text{−}x},x=-1\text{ and }x=1[/latex]
  4. [latex]y=|x|\text{ and }y={x}^{2}[/latex]

For the following exercises (8-10), graph the equations and shade the area of the region between the curves. If necessary, break the region into sub-regions to determine its entire area.

  1. [latex]y=12-x,y=\sqrt{x},\text{ and }y=1[/latex]
  2. [latex]y={x}^{3}\text{ and }y={x}^{2}-2x[/latex] over [latex]x=\left[-1,1\right][/latex]
  3. [latex]y={x}^{3}+3x[/latex] and [latex]y=4x[/latex]

For the following exercises (11-13), graph the equations and shade the area of the region between the curves. Determine its area by integrating over the [latex]y\text{-axis}.[/latex]

  1. [latex]x=2y\text{ and }x={y}^{3}-y[/latex]
  2. [latex]{y}^{2}=x\text{ and }x=y+2[/latex]
  3. [latex]x= \sin y,x= \cos (2y),y=\pi \text{/}2,\text{ and }y=\text{−}\pi \text{/}2[/latex]

For the following exercises (14-19), graph the equations and shade the area of the region between the curves. Determine its area by integrating over the [latex]x[/latex]-axis or [latex]y[/latex]-axis, whichever seems more convenient.

  1. [latex]y=x{e}^{x},y={e}^{x},x=0,\text{ and }x=1[/latex]
  2. [latex]x={y}^{3}+2{y}^{2}+1\text{ and }x=\text{−}{y}^{2}+1[/latex]
  3. [latex]y=4-3x\text{ and }y=\frac{1}{x}[/latex]
  4. [latex]y={x}^{2}-3x+2\text{ and }y={x}^{3}-2{x}^{2}-x+2[/latex]
  5. [latex]y+{y}^{3}=x\text{ and }2y=x[/latex]
  6. [latex]y={ \cos }^{-1}x,y={ \sin }^{-1}x,x=-1,\text{ and }x=1[/latex]

For the following exercises (20-24), find the exact area of the region bounded by the given equations if possible. If you are unable to determine the intersection points analytically, use a calculator to approximate the intersection points with three decimal places and determine the approximate area of the region.

  1. [latex]y={x}^{2}\text{ and }y=\sqrt{1-{x}^{2}}[/latex]
  2. [latex]x=\sqrt{4-{y}^{2}}\text{ and }{y}^{2}=1+{x}^{2}[/latex]
  3. [latex]y={ \sin }^{3}x+2,y= \tan x,x=-1.5,\text{ and }x=1.5[/latex]
  4. [latex]y=\sqrt{1-{x}^{2}}\text{ and }y={x}^{2}+2x+1[/latex]
  5. [latex]y= \cos x,y={e}^{x},x=\text{−}\pi ,\text{ and }x=0[/latex]

For the following exercises (25-28), solve each problem.

  1. A factory selling cell phones has a marginal cost function [latex]C(x)=0.01{x}^{2}-3x+229,[/latex] where [latex]x[/latex] represents the number of cell phones, and a marginal revenue function given by [latex]R(x)=429-2x.[/latex] Find the area between the graphs of these curves and [latex]x=0.[/latex] What does this area represent?
  2. The tortoise versus the hare: The speed of the hare is given by the sinusoidal function [latex]H(t)=1- \cos ((\pi t)\text{/}2)[/latex] whereas the speed of the tortoise is [latex]T(t)=(1\text{/}2){ \tan }^{-1}(t\text{/}4),[/latex] where [latex]t[/latex] is time measured in hours and the speed is measured in miles per hour. Find the area between the curves from time [latex]t=0[/latex] to the first time after one hour when the tortoise and hare are traveling at the same speed. What does it represent? Use a calculator to determine the intersection points, if necessary, accurate to three decimal places.
  3. [latex]y={x}^{2}+2x+1\text{ and }y=\text{−}{x}^{2}-3x+4[/latex]
  4. [latex]x={y}^{2}-2\text{ and }x=2y[/latex]

For the following exercise, solve using calculus, then check your answer with geometry.

  1. Find the area between the perimeter of the unit circle and the triangle created from [latex]y=2x+1,y=1-2x[/latex] and [latex]y=-\frac{3}{5},[/latex] as seen in the following figure. Is there a way to solve this without using calculus?

    This figure is the graph of a circle centered at the origin with radius of 1. There are three lines intersecting the circle. The lines intersect the circle at three points to form a triangle within the circle.

Determining Volumes by Slicing

  1. Derive the formula for the volume of a sphere using the slicing method.
  2. Use the slicing method to derive the formula for the volume of a cone.
  3. Use the slicing method to derive the formula for the volume of a tetrahedron with side length [latex]a.[/latex]
  4. Use the disk method to derive the formula for the volume of a trapezoidal cylinder.
  5. Explain when you would use the disk method versus the washer method. When are they interchangeable?

For the following exercises (6-8), draw a typical slice and find the volume using the slicing method for the given volume.

  1. A pyramid with height [latex]6[/latex] units and square base of side [latex]2[/latex] units, as pictured here.

    This figure is a pyramid with base width of 2 and height of 6 units.

  2. A tetrahedron with a base side of 4 units, as seen here. This figure is an equilateral triangle with side length of 4 units.
  3. A cone of radius [latex]r[/latex] and height [latex]h[/latex] has a smaller cone of radius [latex]r\text{/}2[/latex] and height [latex]h\text{/}2[/latex] removed from the top, as seen here. The resulting solid is called a frustum.

    This figure is a 3-dimensional graph of an upside down cone. The cone is inside of a rectangular prism that represents the xyz coordinate system. the radius of the bottom of the cone is “r” and the radius of the top of the cone is labeled “r/2”.

For the following exercises (9-11), draw an outline of the solid and find the volume using the slicing method.

  1. The base is a triangle with vertices [latex](0,0),(1,0),[/latex] and [latex](0,1).[/latex] Slices perpendicular to the xy-plane are semicircles.
  2. The base is the region under the parabola [latex]y=1-{x}^{2}[/latex] and above the [latex]x\text{-axis}\text{.}[/latex] Slices perpendicular to the [latex]y\text{-axis}[/latex] are squares.
  3. The base is the area between [latex]y=x[/latex] and [latex]y={x}^{2}.[/latex] Slices perpendicular to the [latex]x[/latex]-axis are semicircles.

For the following exercises (12-15), draw the region bounded by the curves. Then, use the disk method to find the volume when the region is rotated around the [latex]x[/latex]-axis.

  1. [latex]y=2{x}^{2},x=0,x=4,\text{ and }y=0[/latex]
  2. [latex]y={x}^{4},x=0,\text{ and }y=1[/latex]
  3. [latex]y= \sin x,y= \cos x,\text{ and }x=0[/latex]
  4. [latex]{x}^{2}-{y}^{2}=9\text{ and }x+y=9,y=0\text{ and }x=0[/latex]

For the following exercises (16-19), draw the region bounded by the curves. Then, find the volume when the region is rotated around the [latex]y[/latex]-axis.

  1. [latex]y=2{x}^{3},x=0,x=1,\text{ and }y=0[/latex]
  2. [latex]y=\sqrt{4-{x}^{2}},y=0,\text{ and }x=0[/latex]
  3. [latex]x= \sec (y)\text{ and }y=\frac{\pi }{4},y=0\text{ and }x=0[/latex]
  4. [latex]y=4-x,y=x,\text{ and }x=0[/latex]

For the following exercises 20-23), draw the region bounded by the curves. Then, find the volume when the region is rotated around the [latex]x[/latex]-axis.

  1. [latex]y={x}^{2}\text{ and }y=x+2[/latex]
  2. [latex]y=4-{x}^{2}\text{ and }y=2-x[/latex]
  3. [latex]y=\sqrt{x}\text{ and }y={x}^{2}[/latex]
  4. [latex]y=\sqrt{1+{x}^{2}}\text{ and }y=\sqrt{4-{x}^{2}}[/latex]

For the following exercises (24-25), draw the region bounded by the curves. Then, use the washer method to find the volume when the region is revolved around the [latex]y[/latex]-axis.

  1. [latex]y=x+2,y=2x-1,\text{ and }x=0[/latex]
  2. [latex]x={e}^{2y},x={y}^{2},y=0,\text{ and }y=\text{ln}(2)[/latex]

For the following exercises (26-28), solve each problem.

  1. Yogurt containers can be shaped like frustums. Rotate the line [latex]y=\frac{1}{m}x[/latex] around the [latex]y[/latex]-axis to find the volume between [latex]y=a\text{ and }y=b.[/latex].

    This figure has two parts. The first part is a solid cone. The base of the cone is wider than the top. It is shown in a 3-dimensional box. Underneath the cone is an image of a yogurt container with the same shape as the figure.

  2. Rotate the ellipse [latex]({x}^{2}\text{/}{a}^{2})+({y}^{2}\text{/}{b}^{2})=1[/latex] around the [latex]y[/latex]-axis to approximate the volume of a football.
  3. What is the volume of the Bundt cake that comes from rotating [latex]y= \sin x[/latex] around the [latex]y[/latex]-axis from [latex]x=0[/latex] to [latex]x=\pi ?[/latex]

    This figure is a graph of a 3-dimensional solid. It is round, bigger towards the bottom. It has a hole in the center that progressively gets smaller towards the bottom. Next to the graph is an image of a bundt cake, resembling the solid.

For the following exercises (29-31), find the volume of the solid described.

  1. The base is the region enclosed by the generic ellipse [latex]({x}^{2}\text{/}{a}^{2})+({y}^{2}\text{/}{b}^{2})=1.[/latex] Slices perpendicular to the [latex]x[/latex]-axis are semicircles.
  2. Find the volume common to two spheres of radius [latex]r[/latex] with centers that are [latex]2h[/latex] apart, as shown here. This figure has two circles that intersect. Both circles have radius “r”. There is a line segment from one center to the other. In the middle of the intersection of the circles is point “h”. It is on the line segment.
  3. Find the volume of a sphere of radius [latex]R[/latex] with a cap of height [latex]h[/latex] removed from the top, as seen here. This figure is a sphere with a top portion removed. The radius of the sphere is “R”. The distance from the center to where the top portion is removed is “R-h”.

Volumes of Revolution: Cylindrical Shells

For the following exercise (1-3), find the volume generated when the region between the two curves is rotated around the given axis. Use both the shell method and the washer method. Use technology to graph the functions and draw a typical slice by hand.

  1. Under the curve of [latex]y=3x,x=0,\text{ and }x=3[/latex] rotated around the [latex]y\text{-axis}.[/latex]
  2. Under the curve of [latex]y=3x,x=0,\text{ and }x=3[/latex] rotated around the [latex]x\text{-axis}.[/latex]
  3. Under the curve of [latex]y=2{x}^{3},x=0,\text{ and }x=2[/latex] rotated around the [latex]x\text{-axis}.[/latex]

For the following exercises (4-8), use shells to find the volumes of the given solids. Note that the rotated regions lie between the curve and the [latex]x[/latex]-axis and are rotated around the [latex]y[/latex]-axis.

  1. [latex]y=5{x}^{3},x=0,\text{ and }x=1[/latex]
  2. [latex]y=\sqrt{1-{x}^{2}},x=0,\text{ and }x=1[/latex]
  3. [latex]y= \sin {x}^{2},x=0,\text{ and }x=\sqrt{\pi }[/latex]
  4. [latex]y=\sqrt{x},x=0,\text{ and }x=1[/latex]
  5. [latex]y=5{x}^{3}-2{x}^{4},x=0,\text{ and }x=2[/latex]

For the following exercises (9-13), use shells to find the volume generated by rotating the regions between the given curve and [latex]y=0[/latex] around the [latex]x\text{-axis}.[/latex]

  1. [latex]y={x}^{2},x=0,\text{ and }x=2[/latex]
  2. [latex]y=\text{ln}(x),x=1,\text{ and }x=e[/latex]
  3. [latex]x=\frac{1+{y}^{2}}{y},y=0,\text{ and }y=2[/latex]
  4. [latex]x={y}^{3}-4{y}^{2},x=-1,\text{ and }x=2[/latex]
  5. [latex]x= \cos y{e}^{y},x=0,\text{ and }x=\pi[/latex]

For the following exercises (14-18), find the volume generated when the region between the curves is rotated around the given axis.

  1. [latex]y={x}^{3},y=0,\text{ and }y=8[/latex] rotated around the [latex]y\text{-axis}.[/latex]
  2. [latex]y=\sqrt{x},x=0,\text{ and }x=1[/latex] rotated around the line [latex]x=2.[/latex]
  3. [latex]y=\sqrt{x}\text{ and }y={x}^{2}[/latex] rotated around the [latex]y\text{-axis}.[/latex]
  4. [latex]x={y}^{3},y=\frac{1}{x},x=1,\text{ and }y=2[/latex] rotated around the [latex]x\text{-axis}.[/latex]
  5. Left of [latex]x= \sin (\pi y),[/latex] right of [latex]y=x,[/latex] around the [latex]y\text{-axis}.[/latex]

For the following exercises (19-22), use technology to graph the region. Determine which method you think would be easiest to use to calculate the volume generated when the function is rotated around the specified axis. Then, use your chosen method to find the volume.

  1. [latex]y= \cos (\pi x),y= \sin (\pi x),x=\frac{1}{4},\text{ and }x=\frac{5}{4}[/latex] rotated around the [latex]y\text{-axis}.[/latex]
  2. [latex]y={x}^{2}-2x,x=2,\text{ and }x=4[/latex] rotated around the [latex]x\text{-axis}.[/latex]
  3. [latex]y=3{x}^{3}-2,y=x,\text{ and }x=2[/latex] rotated around the [latex]y\text{-axis}.[/latex]
  4. [latex]x={y}^{2},x={y}^{2}-2y+1,\text{ and }x=2[/latex] rotated around the [latex]y\text{-axis}.[/latex]

For the following exercises (23-24), use the method of shells to approximate the volumes of some common objects, which are pictured in accompanying figures.

  1. Use the method of shells to find the volume of a cone with radius [latex]r[/latex] and height [latex]h.[/latex] This figure has two images. The first is an upside-down cone with radius r and height h. The second is an ice cream cone.
  2. Use the method of shells to find the volume of a cylinder with radius [latex]r[/latex] and height [latex]h.[/latex] This figure has two images. The first is a cylinder with radius r and height h. The second is a cylindrical candle.

Arc Length of a Curve and Surface Area

For the following exercises (1-2), find the length of the functions over the given interval.

  1. [latex]y=5x\text{ from }x=0\text{ to }x=2[/latex]
  2. [latex]x=4y\text{ from }y=-1\text{ to }y=1[/latex]

For the following exercises (3-7), find the lengths of the functions of [latex]x[/latex] over the given interval. If you cannot evaluate the integral exactly, use technology to approximate it.

  1. [latex]y={x}^{3\text{/}2}[/latex] from [latex](0,0)\text{ to }(1,1)[/latex]
  2. [latex]y=\frac{1}{3}{({x}^{2}+2)}^{3\text{/}2}[/latex] from [latex]x=0\text{ to }x=1[/latex]
  3. [latex]y={e}^{x}[/latex] on [latex]x=0[/latex] to [latex]x=1[/latex]
  4. [latex]y=\frac{{x}^{4}}{4}+\frac{1}{8{x}^{2}}[/latex] from [latex]x=1\text{ to }x=2[/latex]
  5. [latex]y=\frac{1}{27}{(9{x}^{2}+6)}^{3\text{/}2}[/latex] from [latex]x=0\text{ to }x=2[/latex]

For the following exercises (8-12), find the lengths of the functions of [latex]y[/latex] over the given interval. If you cannot evaluate the integral exactly, use technology to approximate it.

  1. [latex]y=\frac{5-3x}{4}[/latex] from [latex]y=0[/latex] to [latex]y=4[/latex]
  2. [latex]x=5{y}^{3\text{/}2}[/latex] from [latex]y=0[/latex] to [latex]y=1[/latex]
  3. [latex]x=\sqrt{y}[/latex] from [latex]y=0\text{ to }y=1[/latex]
  4. [latex]x= \tan y[/latex] from [latex]y=0[/latex] to [latex]y=\frac{3}{4}[/latex]
  5. [latex]x={4}^{y}[/latex] from [latex]y=0\text{ to }y=2[/latex]

For the following exercises (13-16), find the surface area of the volume generated when the following curves revolve around the [latex]x\text{-axis}.[/latex] If you cannot evaluate the integral exactly, use your calculator to approximate it.

  1. [latex]y=\sqrt{x}[/latex] from [latex]x=2[/latex] to [latex]x=6[/latex]
  2. [latex]y=7x[/latex] from [latex]x=-1\text{ to }x=1[/latex]
  3. [latex]y=\sqrt{4-{x}^{2}}[/latex] from [latex]x=0\text{ to }x=2[/latex]
  4. [latex]y=5x[/latex] from [latex]x=1\text{ to }x=5[/latex]

For the following exercises (17-20), find the surface area of the volume generated when the following curves revolve around the [latex]y\text{-axis}\text{.}[/latex] If you cannot evaluate the integral exactly, use your calculator to approximate it.

  1. [latex]y={x}^{2}[/latex] from [latex]x=0\text{ to }x=2[/latex]
  2. [latex]y=x+1[/latex] from [latex]x=0\text{ to }x=3[/latex]
  3. [latex]y=\sqrt[3]{x}[/latex] from [latex]x=1\text{ to }x=27[/latex]
  4. [latex]y=\frac{1}{\sqrt{x}}[/latex] from [latex]x=1[/latex] to [latex]x=3[/latex]

For the following exercises (21-23), solve each problem.

  1. The base of a lamp is constructed by revolving a quarter circle [latex]y=\sqrt{2x-{x}^{2}}[/latex] around the [latex]y\text{-axis}[/latex] from [latex]x=1[/latex] to [latex]x=2,[/latex] as seen here. Create an integral for the surface area of this curve and compute it. This figure is a surface. It is half of a torus created by rotating the curve y=squareroot(2x-x^2) about the x-axis.
  2. A lampshade is constructed by rotating [latex]y=1\text{/}x[/latex] around the [latex]x\text{-axis}[/latex] from [latex]y=1[/latex] to [latex]y=2,[/latex] as seen here. Determine how much material you would need to construct this lampshade—that is, the surface area—accurate to four decimal places. This figure has two images. The first is similar to a frustum of a cone with edges bending inwards. The second is a lamp shade.
  3. You are building a bridge that will span 10 ft. You intend to add decorative rope in the shape of [latex]y=5| \sin ((x\pi )\text{/}5)|,[/latex] where [latex]x[/latex] is the distance in feet from one end of the bridge. Find out how much rope you need to buy, rounded to the nearest foot.

For the following exercises (24-26), find the exact arc length for the following problems over the given interval.

  1. Draw graphs of [latex]y={x}^{2},[/latex] [latex]y={x}^{6},[/latex] and [latex]y={x}^{10}.[/latex] For [latex]y={x}^{n},[/latex] as [latex]n[/latex] increases, formulate a prediction on the arc length from [latex](0,0)[/latex] to [latex](1,1).[/latex] Now, compute the lengths of these three functions and determine whether your prediction is correct.
  2. Solve for the length of [latex]x={y}^{2}[/latex] from [latex](0,0)\text{ to }(1,1).[/latex] Show that [latex]x=(1\text{/}2){y}^{2}[/latex] from [latex](0,0)[/latex] to [latex](2,2)[/latex] is twice as long. Graph both functions and explain why this is so.
  3. Explain why the surface area is infinite when [latex]y=1\text{/}x[/latex] is rotated around the [latex]x\text{-axis}[/latex] for [latex]1\le x<\infty ,[/latex] but the volume is finite.