- Identify the shapes you get from cutting through 3D objects and what 3D shapes are made by spinning flat shapes
Grasping the concepts of cross sections and rotational solids is fundamental in visualizing and understanding the structure of three-dimensional objects. This topic bridges two-dimensional geometry and three-dimensional forms, providing insights into how shapes transform through different perspectives and manipulations.
Identifying Cross Sections of 3D Figures
A cross section is the intersection of a three-dimensional figure with a plane. Analyzing cross sections involves slicing through a 3D object and observing the 2D shape that results from this intersection. The shape of the cross section depends on the orientation of the cutting plane relative to the 3D figure.
Here’s how you can identify cross sections in different 3D figures:
-
Cubes and Rectangular Prisms: When you slice a cube or rectangular prism with a plane parallel to one of its faces, the cross section is a rectangle or a square. A diagonal cut through the cube can yield a triangular or hexagonal cross section, depending on the angle and the dimensions of the cube.

Examples of plane cross-sections of a cube -
Cylinders: Slicing a cylinder with a plane parallel to its base produces a circular cross section. If the plane is perpendicular to the base, the cross section is a rectangle. An angled cut through the cylinder can result in an elliptical cross section.
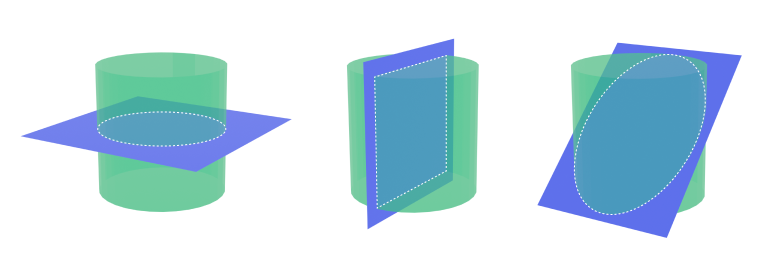
Examples of plane cross-sections of a cylinder -
Cones: A horizontal slice of a cone results in a circle. If the slice is parallel but not aligned with the base, it forms an ellipse. A vertical cut through the cone’s vertex produces a triangular cross section.

Examples of plane cross-sections of a cone -
Spheres: Any plane that cuts through a sphere will always result in a circular cross section.
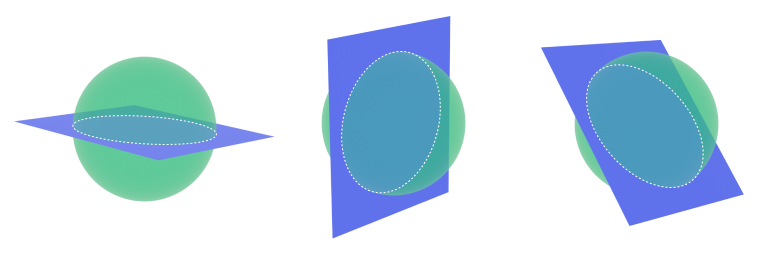
Examples of plane cross-sections of a sphere
cross sections of 3D figures
A cross section is the intersection of a plane with a 3D object. The shape of the cross section depends critically on the geometry of the 3D object and the orientation of the cutting plane.
-
Common Examples:
- Cubes and Rectangular Prisms: Parallel cuts produce rectangles or squares, while diagonal cuts can yield triangles or hexagons.
- Cylinders: Cuts parallel to the base result in circles; perpendicular cuts create rectangles, and angled cuts produce ellipses.
- Cones: Horizontal slices produce circles, slices parallel but off-center yield ellipses, and vertical cuts through the vertex create triangles.
- Spheres: Any cut through a sphere results in a circle, regardless of the angle or position of the plane.
How-To: Determining the Cross Section of a Solid
- Select the Solid and the Plane: Choose the 3D solid you want to examine, and decide the orientation of the slicing plane. This could be parallel, perpendicular, or at an angle to the base or another prominent feature of the solid.
- Visualize the Intersection: Imagine or sketch how the plane cuts through the solid. Consider the symmetry and shape of the solid to predict the shape of the intersection.
- Identify the Shape: Based on the orientation of the plane and the nature of the solid, determine the shape of the cross section. Use geometric properties and previous knowledge of common solids like cylinders, cones, and prisms.
Identify the cross section that is created in the following scenarios:
- A cylinder with a radius of [latex]3[/latex] units and a height of [latex]10[/latex] units is cut along a plane parallel to its base, [latex]4[/latex] units from the top.
- A cone with a base radius of [latex]5[/latex] units and a height of [latex]12[/latex] units is cut horizontally [latex]3[/latex] units down from the apex.
- A sphere with a diameter of [latex]10[/latex] units is cut through the center.
Understanding these cross sections helps in visualizing the internal and external geometries of complex objects, which is crucial in fields such as engineering, architecture, and biology.
Recognizing Solids Formed by Rotating 2D Shapes
Rotational solids are formed when a two-dimensional shape is revolved around an axis. This method is commonly used in both theoretical mathematics and practical applications like engineering and design. Common examples include:
- Rotating a Rectangle: If you rotate a rectangle around one of its sides, you create a cylinder. Rotating it around an axis that bisects the rectangle lengthwise results in a different type of cylindrical shape where the diameters vary.
- Rotating a Triangle: Rotating a right triangle about one of its legs forms a cone. If the rotation is around the hypotenuse, the resulting shape is more complex, typically a sort of truncated cone.
- Rotating a Circle: Rotating a circle around its diameter yields a sphere, which is a fundamental shape in both natural and manufactured objects.
- Rotating a Semicircle: When a semicircle rotates around its diameter, the resulting solid is a sphere; if rotated around its base, the solid is a hemisphere.
rotational solids
Rotational solids are a three-dimensional figure obtained by rotating a two-dimensional shape around an axis that lies in the same plane as the shape.
A revolving door is a practical example of a solid of revolution. These doors, often used in buildings for temperature control and to minimize air leakage, feature multiple panels that rotate around a central shaft. As each panel moves, it traces a cylindrical path, showing how rotating a rectangular panel around a vertical axis creates a cylindrical volume.

How-To: Determining the Shape Formed by Rotation
- Identify the 2D Shape: Begin by recognizing the shape that will be rotated. Common shapes include rectangles, triangles, circles, and semicircles.
- Determine the Axis of Rotation: Note whether the shape rotates around a horizontal or vertical axis, or along one of its edges or through its center.
- Visualize the Rotation: Imagine the 2D shape spinning along the chosen axis. The path traced by the shape’s outer edges forms the surface of the new solid.
- Predict the Solid’s Shape: Based on the rotation, predict the resulting solid’s shape:
- Rectangle rotating around its length forms a cylinder.
- Triangle rotating around a leg forms a cone.
- Circle rotating around its diameter forms a sphere.
Determine the rotational solid formed in the following scenarios:
- A rectangle of dimensions [latex]4[/latex] units by [latex]3[/latex] units is rotated around its longer side
- A right triangle with legs of [latex]3[/latex] units and [latex]4[/latex] units is rotated around its shorter leg.
- A semicircle with a radius of [latex]5[/latex] units is rotated around its diameter.