Related Rates
For the following exercises (1-11), find the quantities for the given equation.
- Find [latex]\frac{dy}{dt}[/latex] at [latex]x=1[/latex] and [latex]y=x^2+3[/latex] if [latex]\frac{dx}{dt}=4[/latex].
- Find [latex]\frac{dz}{dt}[/latex] at [latex](x,y)=(1,3)[/latex] and [latex]z^2=x^2+y^2[/latex] if [latex]\frac{dx}{dt}=4[/latex] and [latex]\frac{dy}{dt}=3[/latex].
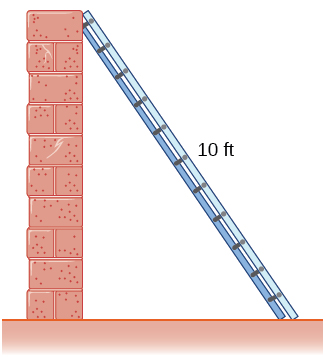
- A [latex]10[/latex] ft ladder is leaning against a wall. If the top of the ladder slides down the wall at a rate of [latex]2[/latex] ft/sec, how fast is the bottom moving along the ground when the bottom of the ladder is [latex]5[/latex] ft from the wall?
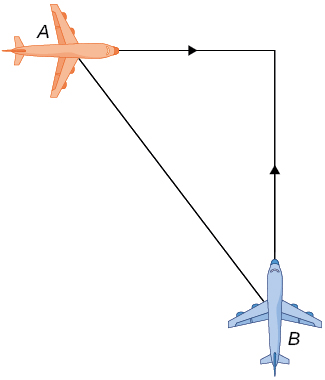
- Two airplanes are flying in the air at the same height: airplane [latex]A[/latex] is flying east at [latex]250[/latex] mi/h and airplane [latex]B[/latex] is flying north at [latex]300[/latex] mi/h. If they are both heading to the same airport, located [latex]30[/latex] miles east of airplane [latex]A[/latex] and [latex]40[/latex] miles north of airplane [latex]B[/latex], at what rate is the distance between the airplanes changing?
- Two buses are driving along parallel freeways that are [latex]5[/latex] mi apart, one heading east and the other heading west. Assuming that each bus drives a constant [latex]55[/latex] mph, find the rate at which the distance between the buses is changing when they are [latex]13[/latex] mi apart, heading toward each other.
- A [latex]6[/latex]-ft-tall person walks away from a [latex]10[/latex] ft lamppost at a constant rate of [latex]3[/latex] ft/sec. What is the rate that the tip of the shadow moves away from the pole when the person is [latex]10[/latex] ft away from the pole?
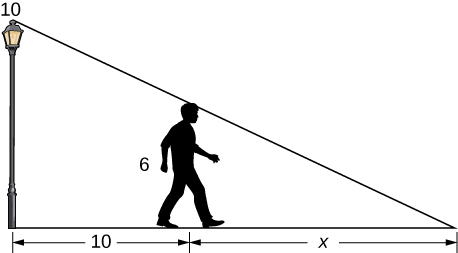
- Using the previous problem, what is the rate at which the tip of the shadow moves away from the person when the person is [latex]10[/latex] ft from the pole?
- A [latex]5[/latex]-ft-tall person walks toward a wall at a rate of [latex]2[/latex] ft/sec. A spotlight is located on the ground [latex]40[/latex] ft from the wall. How fast does the height of the person’s shadow on the wall change when the person is [latex]10[/latex] ft from the wall?
- Using the previous problem, what is the rate at which the shadow changes when the person is [latex]10[/latex] ft from the wall, if the person is walking away from the wall at a rate of [latex]2[/latex] ft/sec?
- A helicopter starting on the ground is rising directly into the air at a rate of [latex]25[/latex] ft/sec. You are running on the ground starting directly under the helicopter at a rate of [latex]10[/latex] ft/sec. Find the rate of change of the distance between the helicopter and yourself after [latex]5[/latex] sec.
- Using the previous problem, what is the rate at which the distance between you and the helicopter is changing when the helicopter has risen to a height of [latex]60[/latex] ft in the air, assuming that, initially, it was [latex]30[/latex] ft above you?
For the following exercises (12-15), draw and label diagrams to help solve the related-rates problems.
- The volume of a cube decreases at a rate of [latex]10[/latex] m3/s. Find the rate at which the side of the cube changes when the side of the cube is [latex]2[/latex] m.
- The radius of a sphere decreases at a rate of [latex]3[/latex] m/sec. Find the rate at which the surface area decreases when the radius is [latex]10[/latex] m.
- The radius of a sphere is increasing at a rate of [latex]9[/latex] cm/sec. Find the radius of the sphere when the volume and the radius of the sphere are increasing at the same numerical rate.
- A triangle has two constant sides of length [latex]3[/latex] ft and [latex]5[/latex] ft. The angle between these two sides is increasing at a rate of [latex]0.1[/latex] rad/sec. Find the rate at which the area of the triangle is changing when the angle between the two sides is [latex]\pi /6[/latex].
For the following exercises (16-19), consider a right cone that is leaking water. The dimensions of the conical tank are a height of 16 ft and a radius of 5 ft.
- How fast does the depth of the water change when the water is [latex]10[/latex] ft high if the cone leaks water at a rate of [latex]10[/latex] [latex]\text{ft}^3[/latex]/min?
- If the water level is decreasing at a rate of [latex]3[/latex] in/min when the depth of the water is [latex]8[/latex] ft, determine the rate at which water is leaking out of the cone.
- A cylinder is leaking water but you are unable to determine at what rate. The cylinder has a height of [latex]2[/latex] m and a radius of [latex]2[/latex] m. Find the rate at which the water is leaking out of the cylinder if the rate at which the height is decreasing is [latex]10[/latex] cm/min when the height is [latex]1[/latex] m.
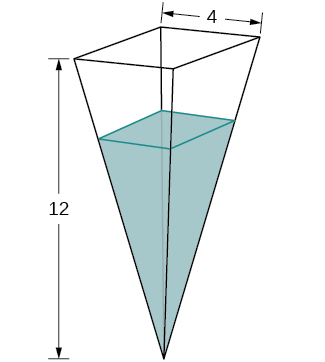
- A tank is shaped like an upside-down square pyramid, with base of [latex]4[/latex] m by [latex]4[/latex] m and a height of [latex]12[/latex] m (see the following figure). How fast does the height increase when the water is [latex]2[/latex] m deep if water is being pumped in at a rate of [latex]\frac{2}{3} \, \text{m}^3[/latex]/sec?
For the following exercises (20-22), draw the situations and solve the related-rate problems.
- You are stationary on the ground and are watching a bird fly horizontally at a rate of [latex]10[/latex] m/sec. The bird is located [latex]40[/latex] m above your head. How fast does the angle of elevation change when the horizontal distance between you and the bird is [latex]9[/latex] m?
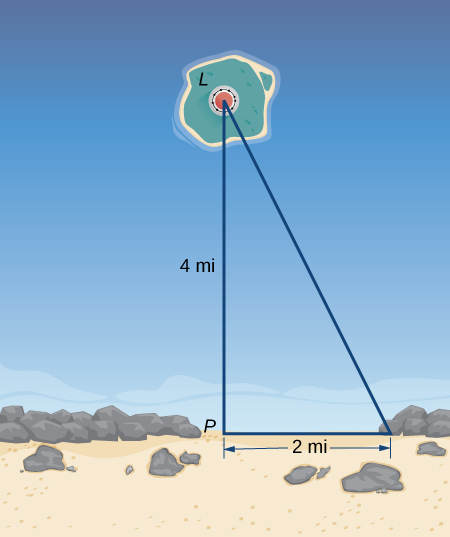
- A lighthouse, [latex]L[/latex], is on an island [latex]4[/latex] mi away from the closest point, [latex]P[/latex], on the beach (see the following image). If the lighthouse light rotates clockwise at a constant rate of [latex]10[/latex] revolutions/min, how fast does the beam of light move across the beach [latex]2[/latex] mi away from the closest point on the beach?
- You are walking to a bus stop at a right-angle corner. You move north at a rate of [latex]2[/latex] m/sec and are [latex]20[/latex] m south of the intersection. The bus travels west at a rate of [latex]10[/latex] m/sec away from the intersection – you have missed the bus! What is the rate at which the angle between you and the bus is changing when you are [latex]20[/latex] m south of the intersection and the bus is [latex]10[/latex] m west of the intersection?
For the following exercises (23-24), refer to the figure of baseball diamond, which has sides of [latex]90[/latex] ft.
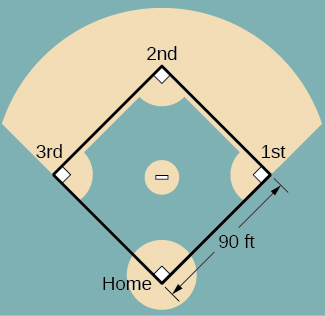
- A batter hits a ball toward second base at [latex]80[/latex] ft/sec and runs toward first base at a rate of [latex]30[/latex] ft/sec. At what rate does the distance between the ball and the batter change when the runner has covered one-third of the distance to first base? (Hint: Recall the law of cosines.)
- Runners start at first and second base. When the baseball is hit, the runner at first base runs at a speed of [latex]18[/latex] ft/sec toward second base and the runner at second base runs at a speed of [latex]20[/latex] ft/sec toward third base. How fast is the distance between runners changing [latex]1[/latex] sec after the ball is hit?
Linear Approximations and Differentials
- What is the linear approximation for any generic linear function [latex]y=mx+b[/latex]?
- Determine the necessary conditions such that the linear approximation function is constant. Use a graph to prove your result.
- Explain why the linear approximation becomes less accurate as you increase the distance between [latex]x[/latex] and [latex]a[/latex]. Use a graph to prove your argument.
- When is the linear approximation exact?
For the following exercises (5-7), find the linear approximation [latex]L(x)[/latex] to [latex]y=f(x)[/latex] near [latex]x=a[/latex] for the function.
- [latex]f(x)=\frac{1}{x}, \, a=2[/latex]
- [latex]f(x)= \sin x, \, a=\frac{\pi }{2}[/latex]
- [latex]f(x)= \sin^2 x, \, a=0[/latex]
For the following exercises (8-10), compute the values given within 0.01 by deciding on the appropriate [latex]f(x)[/latex] and [latex]a[/latex], and evaluating [latex]L(x)=f(a)+f^{\prime}(a)(x-a)[/latex]. Check your answer using a calculator.
- [latex]\sin (0.02)[/latex]
- [latex](15.99)^{1/4}[/latex]
- [latex]\sin (3.14)[/latex]
For the following exercises (11-13), determine the appropriate [latex]f(x)[/latex] and [latex]a[/latex], and evaluate [latex]L(x)=f(a)+f^{\prime}(a)(x-a).[/latex] Calculate the numerical error in the linear approximations that follow.
- [latex]\cos (0.01)[/latex]
- [latex](1.01)^{-3}[/latex]
- [latex]\sqrt{8.99}[/latex]
For the following exercises (14-18), find the differential of the function.
- [latex]y=x \cos x[/latex]
- [latex]y=\frac{x^2+2}{x-1}[/latex]
- [latex]y=\frac{1}{x+1}[/latex], [latex]x=1[/latex], [latex]dx=0.25[/latex]
- [latex]y=\frac{3x^2+2}{\sqrt{x+1}}[/latex], [latex]x=0[/latex], [latex]dx=0.1[/latex]
- [latex]y=x^3+2x+\frac{1}{x}[/latex], [latex]x=1[/latex], [latex]dx=0.05[/latex]
For the following exercises (19-21), find the change in volume [latex]dV[/latex] or in surface area [latex]dA[/latex].
- [latex]dA[/latex] if the sides of a cube change from [latex]x[/latex] to [latex]x+dx[/latex].
- [latex]dV[/latex] if the radius of a sphere changes from [latex]r[/latex] by [latex]dr[/latex].
- [latex]dV[/latex] if a circular cylinder of height [latex]3[/latex] changes from [latex]r=2[/latex] to [latex]r=1.9[/latex] cm.
For the following exercise, use differentials to estimate the maximum and relative error when computing the surface area or volume.
- A pool has a rectangular base of [latex]10[/latex] ft by [latex]20[/latex] ft and a depth of [latex]6[/latex] ft. What is the change in volume if you only fill it up to [latex]5.5[/latex] ft?
For the following exercises (23-25), confirm the approximations by using the linear approximation at [latex]x=0[/latex].
- [latex]\sqrt{1-x}\approx 1-\frac{1}{2}x[/latex]
- [latex]\frac{1}{\sqrt{1-x^2}}\approx 1[/latex]
- [latex]\sqrt{c^2+x^2}\approx c[/latex]
Maxima and Minima
- If you are finding an absolute minimum over an interval [latex][a,b][/latex], why do you need to check the endpoints? Draw a graph that supports your hypothesis.
- When you are checking for critical points, explain why you also need to determine points where [latex]f^{\prime}(x)[/latex] is undefined. Draw a graph to support your explanation.
- Can you have a finite absolute maximum for [latex]y=ax^3+bx^2+cx+d[/latex] over [latex](−\infty ,\infty )[/latex] assuming [latex]a[/latex] is non-zero? Explain why or why not using graphical arguments.
- Is it possible to have more than one absolute maximum? Use a graphical argument to prove your hypothesis.
- Graph the function [latex]y=e^{ax}[/latex]. For which values of [latex]a[/latex], on any infinite domain, will you have an absolute minimum and absolute maximum?
For the following exercises (6-7), determine where the local and absolute maxima and minima occur on the graph given. Assume the graph represents the entirety of each function.
For the following problems (8-9), draw graphs of [latex]f(x)[/latex], which is continuous, over the interval [latex][-4,4][/latex] with the following properties:
- Absolute minimum at [latex]x=1[/latex] and absolute maximum at [latex]x=2[/latex]
- Absolute maxima at [latex]x=2[/latex] and [latex]x=-3[/latex], local minimum at [latex]x=1[/latex], and absolute minimum at [latex]x=4[/latex]
For the following exercises (10-14), find the critical points in the domains of the following functions.
- [latex]y=4\sqrt{x}-x^2[/latex]
- [latex]y=\ln (x-2)[/latex]
- [latex]y=\sqrt{4-x^2}[/latex]
- [latex]y=\frac{x^2-1}{x^2+2x-3}[/latex]
- [latex]y=x+\frac{1}{x}[/latex]
For the following exercises (15-19), find the local and/or absolute maxima for the functions over the specified domain.
- [latex]y=x^2+\frac{2}{x}[/latex] over [latex][1,4][/latex]
- [latex]y=\frac{1}{(x-x^2)}[/latex] over [latex](0,1)[/latex]
- [latex]y=x+ \sin (x)[/latex] over [latex][0,2\pi][/latex]
- [latex]y=|x+1|+|x-1|[/latex] over [latex][-3,2][/latex]
- [latex]y= \sin x+ \cos x[/latex] over [latex][0,2\pi][/latex]
For the following exercises (20-22), find the local and absolute minima and maxima for the functions over [latex](−\infty ,\infty )[/latex].
- [latex]y=x^2+4x+5[/latex]
- [latex]y=3x^4+8x^3-18x^2[/latex]
- [latex]y=\dfrac{x^2+x+6}{x-1}[/latex]
For the following functions (23-25), use a calculator to graph the function and to estimate the absolute and local maxima and minima. Then, solve for them explicitly.
- [latex]y=3x\sqrt{1-x^2}[/latex]
- [latex]y=12x^5+45x^4+20x^3-90x^2-120x+3[/latex]
- [latex]y=\dfrac{\sqrt{4-x^2}}{\sqrt{4+x^2}}[/latex]
Find the critical points, maxima, and minima for the following piecewise function.
- [latex]y=\begin{cases} x^2+1, & x\le 1\\ x^2-4x+5, & x>1 \end{cases}[/latex]
For the following exercise, find the critical points of the following generic functions. Are they maxima, minima, or neither? State the necessary conditions.
- [latex]y=(x-1)^a[/latex], given that [latex]a>1[/latex]
The Mean Value Theorem
- Why do you need continuity to apply the Mean Value Theorem? Construct a counterexample.
- Why do you need differentiability to apply the Mean Value Theorem? Find a counterexample.
- When are Rolle’s theorem and the Mean Value Theorem equivalent?
- If you have a function with a discontinuity, is it still possible to have [latex]f^{\prime}(c)(b-a)=f(b)-f(a)[/latex]? Draw such an example or prove why not.
For the following exercises (5-6), determine over what intervals (if any) the Mean Value Theorem applies. Justify your answer.
- [latex]y=\frac{1}{x^3}[/latex]
- [latex]y=\sqrt{x^2-4}[/latex]
For the following exercises (7-8), graph the functions on a calculator and draw the secant line that connects the endpoints. Estimate the number of points [latex]c[/latex] such that [latex]f^{\prime}(c)(b-a)=f(b)-f(a)[/latex].
- [latex]y=3x^3+2x+1[/latex] over [latex][-1,1][/latex]
- [latex]y=x^2 \cos (\pi x)[/latex] over [latex][-2,2][/latex]
For the following exercises (9-11), use the Mean Value Theorem and find all points [latex]0 < c < 2[/latex] such that [latex]f(2)-f(0)=f^{\prime}(c)(2-0)[/latex].
- [latex]f(x)=x^3[/latex]
- [latex]f(x)= \cos (2\pi x)[/latex]
- [latex]f(x)=(x-1)^{10}[/latex]
For the following exercises (12-13), show there is no [latex]c[/latex] such that [latex]f(1)-f(-1)=f^{\prime}(c)(2)[/latex]. Explain why the Mean Value Theorem does not apply over the interval [latex][-1,1][/latex]
- [latex]f(x)=|x-\frac{1}{2}|[/latex]
- [latex]f(x)=\sqrt{|x|}[/latex]
For the following exercises (14-19), determine whether the Mean Value Theorem applies for the functions over the given interval [latex][a,b][/latex]. Justify your answer.
- [latex]y=e^x[/latex] over [latex][0,1][/latex]
- [latex]f(x)= \tan (2\pi x)[/latex] over [latex][0,2][/latex]
- [latex]y=\dfrac{1}{|x+1|}[/latex] over [latex][0,3][/latex]
- [latex]y=\dfrac{x^2+3x+2}{x}[/latex] over [latex][-1,1][/latex]
- [latex]y=\ln (x+1)[/latex] over [latex][0,e-1][/latex]
- [latex]y=5+|x|[/latex] over [latex][-1,1][/latex]
For the following exercises (20-24), use a calculator to graph the function over the interval [latex][a,b][/latex] and graph the secant line from [latex]a[/latex] to [latex]b[/latex]. Use the calculator to estimate all values of [latex]c[/latex] as guaranteed by the Mean Value Theorem. Then, find the exact value of [latex]c[/latex], if possible, or write the final equation and use a calculator to estimate to four digits.
- [latex]y= \tan (\pi x)[/latex] over [latex][-\frac{1}{4},\frac{1}{4}][/latex]
- [latex]y=|x^2+2x-4|[/latex] over [latex][-4,0][/latex]
- [latex]y=\sqrt{x+1}+\frac{1}{x^2}[/latex] over [latex][3,8][/latex]
- Two cars drive from one spotlight to the next, leaving at the same time and arriving at the same time. Is there ever a time when they are going the same speed? Prove or disprove.
- Show that [latex]y= \csc^2 x[/latex] and [latex]y= \cot^2 x[/latex] have the same derivative. What can you say about [latex]y= \csc^2 x - \cot^2 x[/latex]?
Derivatives and the Shape of a Graph
- If [latex]c[/latex] is a critical point of [latex]f(x)[/latex], when is there no local maximum or minimum at [latex]c[/latex]? Explain.
- For the function [latex]y=x^3[/latex], is [latex]x=0[/latex] both an inflection point and a local maximum/minimum?
- For the function [latex]y=x^3[/latex], is [latex]x=0[/latex] an inflection point?
- Is it possible for a point [latex]c[/latex] to be both an inflection point and a local extrema of a twice differentiable function?
- Why do you need continuity for the first derivative test? Come up with an example.
- Explain whether a concave-down function has to cross [latex]y=0[/latex] for some value of [latex]x[/latex].
- Explain whether a polynomial of degree [latex]2[/latex] can have an inflection point.
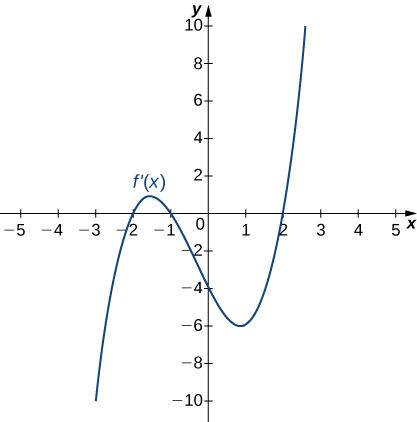
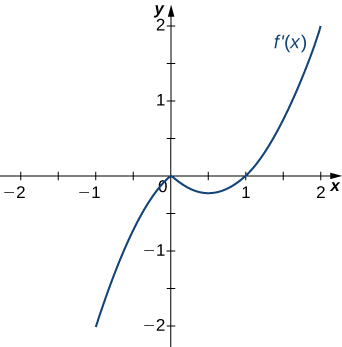
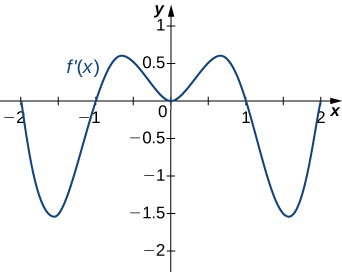
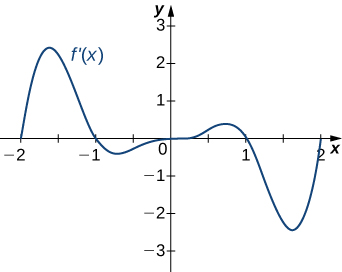
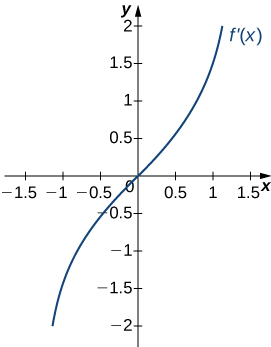
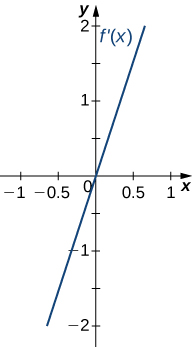
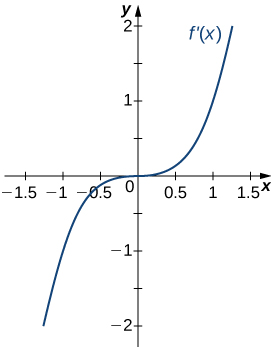
For the following exercises (8-10), analyze the graphs of [latex]f^{\prime}[/latex], then list all intervals where [latex]f[/latex] is increasing or decreasing.
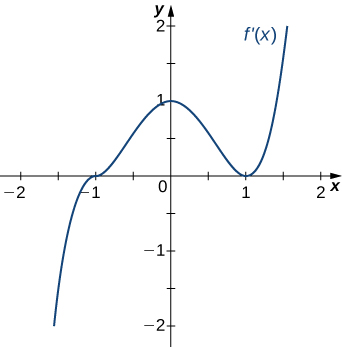
For the following exercises (11-12), analyze the graphs of [latex]f^{\prime}[/latex], then list
- all intervals where [latex]f[/latex] is increasing and decreasing and
- where the minima and maxima are located.
For the following exercises (13-15), analyze the graphs of [latex]f^{\prime}[/latex], then list all inflection points and intervals [latex]f[/latex] that are concave up and concave down.
For the following exercises (16-17), draw a graph that satisfies the given specifications for the domain [latex]x=[-3,3][/latex]. The function does not have to be continuous or differentiable.
- [latex]f^{\prime}(x)>0[/latex] over [latex]x>2, \, -3
- There is a local maximum at [latex]x=2[/latex], local minimum at [latex]x=1[/latex], and the graph is neither concave up nor concave down.
For the following exercise, determine,
- intervals where [latex]f[/latex] is concave up or concave down
- the inflection points of [latex]f[/latex].
- [latex]f(x)=x^3-4x^2+x+2[/latex]
For the following exercises (19-21), determine
- intervals where [latex]f[/latex] is increasing or decreasing,
- local minima and maxima of [latex]f[/latex],
- intervals where [latex]f[/latex] is concave up and concave down, and
- the inflection points of [latex]f[/latex].
- [latex]f(x)=x^3-6x^2[/latex]
- [latex]f(x)=x^{11}-6x^{10}[/latex]
- [latex]f(x)=x^2+x+1[/latex]
For the following exercises (22-26), determine,
- intervals where [latex]f[/latex] is increasing or decreasing,
- local minima and maxima of [latex]f[/latex],
- intervals where [latex]f[/latex] is concave up and concave down, and
- the inflection points of [latex]f[/latex]. Sketch the curve, then use a calculator to compare your answer. If you cannot determine the exact answer analytically, use a calculator.
- [latex]f(x)= \sin (\pi x)- \cos (\pi x)[/latex] over [latex]x=[-1,1][/latex]
- [latex]f(x)= \sin x+ \tan x[/latex] over [latex]\left(-\frac{\pi }{2},\frac{\pi }{2}\right)[/latex]
- [latex]f(x)=\dfrac{1}{1-x}, \, x \ne 1[/latex]
- [latex]f(x)= \sin x e^x[/latex] over [latex]x=[−\pi ,\pi][/latex]
- [latex]f(x)=\frac{1}{4}\sqrt{x}+\frac{1}{x}, \, x>0[/latex]
For the following exercises (27-29), interpret the sentences in terms of [latex]f, \, f^{\prime}[/latex], and [latex]f^{\prime \prime}[/latex].
- The population is growing more slowly. Here [latex]f[/latex] is the population. [
- The airplane lands smoothly. Here [latex]f[/latex] is the plane’s altitude.
- The economy is picking up speed. Here [latex]f[/latex] is a measure of the economy, such as GDP.
For the following exercises (30-31), consider a third-degree polynomial [latex]f(x)[/latex], which has the properties [latex]f^{\prime}(1)=0, \, f^{\prime}(3)=0[/latex]. Determine whether the following statements are true or false. Justify your answer.
- [latex]f^{\prime \prime}(x)=0[/latex] for some [latex]1 \le x \le 3[/latex]
- If [latex]f(x)[/latex] has three roots, then it has [latex]1[/latex] inflection point.