A Preview of Calculus: Learn It 2

The Tangent Problem and Differential Calculus Cont.

The Secant Line

We can approximate the rate of change of a function [latex]f(x)[/latex] at a point [latex](a,f(a))[/latex] on its graph by taking another point [latex](x,f(x))[/latex] on the graph of [latex]f(x)[/latex], drawing a line through the two points, and calculating the slope of the resulting line. Such a line is called a secant line.

secant line

The secant to the function [latex]f(x)[/latex] through the points [latex](a,f(a))[/latex] and [latex](x,f(x))[/latex] is the line passing through these points. Its slope is given by

[latex]m_{\sec}=\dfrac{f(x)-f(a)}{x-a}[/latex]

The figure below shows a secant line to a function [latex]f(x)[/latex] at a point [latex](a,f(a))[/latex].

A graph showing a generic curved function going through the points (0,0), (a, fa.), and (x, f(x)). A straight line called the secant line is drawn through the points (a, fa.), and (x, f(x)), going below the curved function between a and x and going above the curved function at values greater than x or less than a. The curved function and the secant line cross once more at some point in the third quadrant. The slope of the secant line is ( f(x) – fa. ) / (x – a).
Figure 3. The slope of a secant line through a point [latex](a,f(a))[/latex] estimates the rate of change of the function at the point [latex](a,f(a))[/latex].

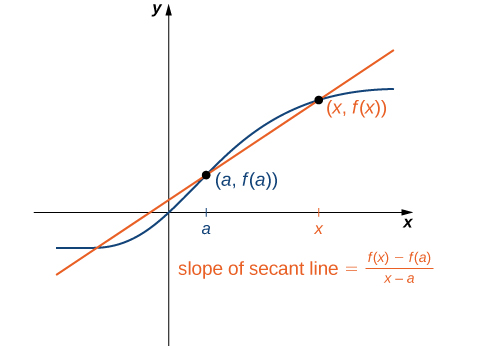
The accuracy of approximating the rate of change of the function with a secant line depends on how close [latex]x[/latex] is to [latex]a[/latex]. As we see in Figure 4, if [latex]x[/latex] is closer to [latex]a[/latex], the slope of the secant line is a better measure of the rate of change of [latex]f(x)[/latex] at [latex]a[/latex].

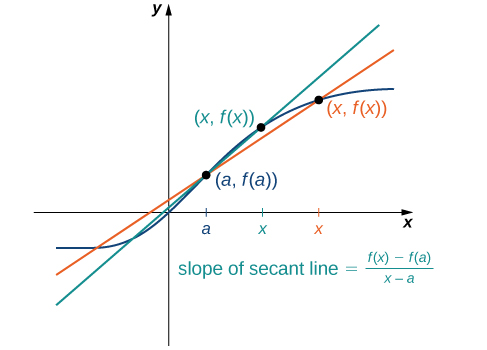
This graph is the same as the previous secant line and generic curved function graph. However, another point x is added, this time plotted closer to a on the x-axis. As such, another secant line is drawn through the points (a, fa.) and the new, closer (x, f(x)). The line stays much closer to the generic curved function around (a, fa.). The slope of this secant line has become a better approximation of the rate of change of the generic function.
Figure 4. As x gets closer to a, the slope of the secant line becomes a better approximation to the rate of change of the function [latex]f(x)[/latex] at a.

The Tangent Line

The secant lines approach a specific line known as the function’s tangent at point . The slope of this tangent line indicates the function’s rate of change at that point. This value corresponds to the function’s derivative at [latex]a[/latex], or the rate of change of the function at [latex]a[/latex]. This concept is at the heart of differential calculus, which delves into derivatives and their various applications.

tangent line

The tangent line at a point on a function’s graph provides a visual representation of the derivative at that point. It reflects the instantaneous rate of change of the function.

As a function’s value incrementally changes, secant lines are drawn between two points on the function’s curve, approximating the slope between them. As one point on the secant line moves closer to the other, the secant line approaches the tangent line at that point.

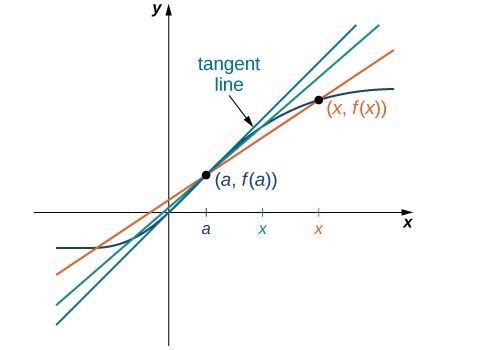
This graph is a continuation of the previous two. This time, the graph contains the curved function, the two secant lines, and a tangent line. As x approaches a, the secant lines approach the tangent line.
Figure 5. Solving the Tangent Problem: As x approaches a, the secant lines approach the tangent line.

This process demonstrates how the slope of the tangent line at a particular point [latex]a[/latex] is the limit of the slopes of the secant lines, providing the derivative of the function at [latex]a[/latex], denoted by [latex]f′(a)[/latex].

Estimate the slope of the tangent line (rate of change) to [latex]f(x)=x^2[/latex] at [latex]x=1[/latex] by finding slopes of secant lines through [latex](1,1)[/latex] and each of the following points on the graph of [latex]f(x)=x^2[/latex].

  1. [latex](2,4)[/latex]
  2. [latex]\left(\frac{3}{2},\frac{9}{4}\right)[/latex]