Substitution

1.  
2. $u=h(x)$
3. $du=8xdx;f(u)=\frac{1}{8\sqrt{u}}$
4. $\frac{1}{5}{(x+1)}^{5}+C$
5. $-\frac{1}{12{(3-2x)}^{6}}+C$
6. $\sqrt{{x}^{2}+1}+C$
7. $\frac{1}{8}{({x}^{2}-2x)}^{4}+C$
8. $\sin \theta -\frac{{ \sin }^{3}\theta }{3}+C$
9. $\frac{{(1-x)}^{101}}{101}-\frac{{(1-x)}^{100}}{100}+C$
10. $-\frac{1}{22(7-11{x}^{2})}+C$
11. $-\frac{{ \cos }^{4}\theta }{4}+C$
12. $-\frac{{ \cos }^{3}(\pi t)}{3\pi }+C$
13. $-\frac{1}{4}\phantom{\rule{0.05em}{0ex}}{ \cos }^{2}({t}^{2})+C$
14. $-\frac{1}{3({x}^{3}-3)}+C$
15. $-\frac{2({y}^{3}-2)}{3\sqrt{1-{y}^{3}}}$
16. $\frac{1}{33}{(1-{ \cos }^{3}\theta )}^{11}+C$
17. $\frac{1}{12}{({ \sin }^{3}\theta -3{ \sin }^{2}\theta )}^{4}+C$
18. ${L}_{50}=-8.5779.$ The exact area is $\frac{-81}{8}$
19. ${L}_{50}=-0.006399$ … The exact area is $0$.
20. $u=1+{x}^{2},du=2xdx,\frac{1}{2}{\displaystyle\int }_{1}^{2}{u}^{-1\text{/}2}du=\sqrt{2}-1$
21. $u=1+{t}^{3},du=3{t}^{2}du,\frac{1}{3}{\displaystyle\int }_{1}^{2}{u}^{-1\text{/}2}du=\frac{2}{3}(\sqrt{2}-1)$
22. $u= \cos \theta ,du=\text{−} \sin \theta d\theta ,{\displaystyle\int }_{1\text{/}\sqrt{2}}^{1}{u}^{-4}du=\frac{1}{3}(2\sqrt{2}-1)$
23. 
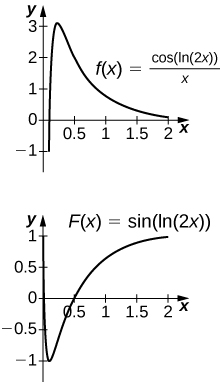
    The antiderivative is $y= \sin (\text{ln}(2x)).$ Since the antiderivative is not continuous at $x=0,$ one cannot find a value of C that would make $y= \sin (\text{ln}(2x))-C$ work as a definite integral.
24. 
    The antiderivative is $y=\frac{1}{2}\phantom{\rule{0.05em}{0ex}}{ \sec }^{2}x.$ You should take $C=-2$ so that $F(-\frac{\pi }{3})=0.$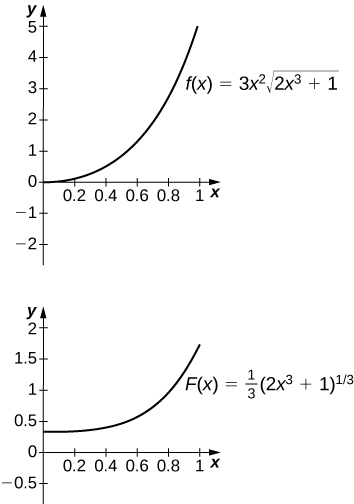
25. 
    The antiderivative is $y=\frac{1}{3}{(2{x}^{3}+1)}^{3\text{/}2}.$ One should take $C=-\frac{1}{3}.$
26. No, because the integrand is discontinuous at $x=1.$
27. $u= \sin ({t}^{2});$ the integral becomes $\frac{1}{2}{\displaystyle\int }_{0}^{0}udu.$
28. $u=(1+{(t-\frac{1}{2})}^{2});$ the integral becomes $\text{−}{\displaystyle\int }_{5\text{/}4}^{5\text{/}4}\frac{1}{u}du.$
29. $u=1-t;$ the integral becomes

    $\begin{array}{l}{\displaystyle\int }_{1}^{-1}u \cos (\pi (1-u))du\hfill \\ ={\displaystyle\int }_{1}^{-1}u\left[ \cos \pi \cos u- \sin \pi \sin u\right]du\hfill \\ =\text{−}{\displaystyle\int }_{1}^{-1}u \cos udu\hfill \\ ={\displaystyle\int }_{-1}^{1}u \cos udu=0\hfill \end{array}$
    since the integrand is odd.

30. Setting $u=cx$ and $du=cdx$ gets you $\frac{1}{\frac{b}{c}-\frac{a}{c}}{\displaystyle\int }_{a\text{/}c}^{b\text{/}c}f(cx)dx=\frac{c}{b-a}{\displaystyle\int }_{u=a}^{u=b}f(u)\frac{du}{c}=\frac{1}{b-a}{\displaystyle\int }_{a}^{b}f(u)du.$
31. ${\displaystyle\int }_{0}^{x}g(t)dt=\frac{1}{2}{\displaystyle\int }_{u=1-{x}^{2}}^{1}\frac{du}{{u}^{a}}=\frac{1}{2(1-a)}{u}^{1-a}{|}_{u=1-{x}^{2}}^{1}=\frac{1}{2(1-a)}(1-{(1-{x}^{2})}^{1-a}).$ As $x\to 1$ the limit is $\frac{1}{2(1-a)}$ if $a<1,$ and the limit diverges to +∞ if $a>1.$
32. ${\displaystyle\int }_{t=\pi }^{0}b\sqrt{1-{ \cos }^{2}t}×(\text{−}a \sin t)dt={\displaystyle\int }_{t=0}^{\pi }ab{ \sin }^{2}tdt$
33. $f(t)=2 \cos (3t)- \cos (2t);{\displaystyle\int }_{0}^{\pi \text{/}2}(2 \cos (3t)- \cos (2t))=-\frac{2}{3}$

Integrals Involving Exponential and Logarithmic Functions

1. $\frac{1}{9}{x}^{3}(\text{ln}({x}^{3})-1)+C$
2. $2\sqrt{x}(\text{ln}x-2)+C$
3. ${\displaystyle\int }_{0}^{\text{ln}x}{e}^{t}dt={e}^{t}{|}_{0}^{\text{ln}x}={e}^{\text{ln}x}-{e}^{0}=x-1$
4. $-\frac{1}{3}\text{ln}( \sin (3x)+ \cos (3x))$
5. $-\frac{1}{2}\text{ln}| \csc ({x}^{2})+ \cot ({x}^{2})|+C$
6. $-\frac{1}{2}{(\text{ln}( \csc x))}^{2}+C$
7. $\frac{1}{3}\text{ln}(\frac{26}{7})$
8. $y-2\text{ln}|y+1|+C$
9. $\text{ln}| \sin x- \cos x|+C$
10. $-\frac{1}{3}{(1-(\text{ln}{x}^{2}))}^{3\text{/}2}+C$
11. Exact solution: $\frac{e-1}{e},{R}_{50}=0.6258.$ Since $f$ is decreasing, the right endpoint estimate underestimates the area.
12. Exact solution: $\frac{2\text{ln}(3)-\text{ln}(6)}{2},{R}_{50}=0.2033.$ Since $f$ is increasing, the right endpoint estimate overestimates the area.
13. Exact solution: $-\frac{1}{\text{ln}(4)},{R}_{50}=-0.7164.$ Since $f$ is increasing, the right endpoint estimate overestimates the area (the actual area is a larger negative number).

Integrals Resulting in Inverse Trigonometric

1. ${ \sin }^{-1}x{|}_{0}^{\sqrt{3}\text{/}2}=\frac{\pi }{3}$
2. ${ \tan }^{-1}x{|}_{\sqrt{3}}^{1}=-\frac{\pi }{12}$
3. ${ \sec }^{-1}x{|}_{1}^{\sqrt{2}}=\frac{\pi }{4}$