The Squeeze Theorem Cont.
We now use the squeeze theorem to tackle several very important limits. Although this discussion is somewhat lengthy, these limits prove invaluable for the development of the material in both the next section and the next module. The first of these limits is [latex]\underset{\theta \to 0}{\lim} \sin \theta[/latex].
Evaluating the Limit of Sine as Theta Approaches Zero
Consider the behavior of [latex]\sin(\theta)[/latex] as [latex]\theta[/latex] approaches zero. On the unit circle, [latex]\sin(\theta)[/latex] corresponds to the [latex]y[/latex]-coordinate, which also represents the arc’s height for a given angle, [latex]\theta[/latex].
As [latex]\theta[/latex] gets closer to zero, particularly for [latex]0 < \theta < \frac{\pi}{2}[/latex], [latex]\sin(\theta)[/latex] becomes smaller and approaches the angle’s measure itself, meaning [latex]\sin(\theta)[/latex] is squeezed between [latex]0[/latex] and [latex]\theta[/latex] .
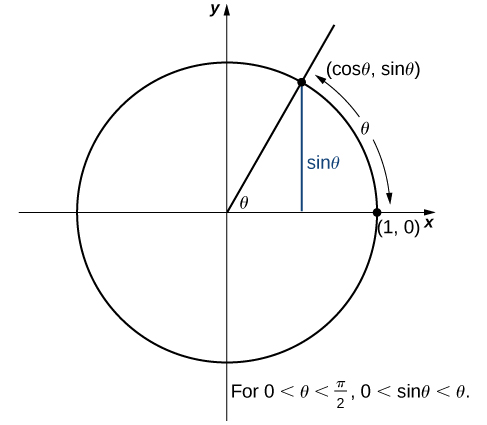
First, consider the established inequalities for [latex]\sin(\theta)[/latex] when [latex]\theta[/latex] is between [latex]0[/latex] and [latex]\frac{\pi}{2}[/latex]:
[latex]0 < \theta < \frac{\pi}{2} \Longrightarrow 0 < \sin \theta < \theta[/latex]
Now, as [latex]\theta[/latex] approaches zero from the positive direction, we know that [latex]\sin(\theta)[/latex] also approaches zero because it is sandwiched between [latex]0[/latex] and [latex]\theta[/latex].
Mathematically, this can be expressed as:
[latex]\underset{\theta \to 0^+}{\lim}0=0 \text{ and }\underset{\theta \to 0^+}{\lim} \theta =0[/latex],
which, according to the Squeeze Theorem, compels [latex]\sin(\theta)[/latex] to satisfy:
The same principle applies when approaching zero from the negative side, where [latex]\sin(\theta)[/latex] is negative but greater than [latex]-\theta[/latex]:
the limit of [latex]\sin(\theta)[/latex]
[latex]\underset{\theta \to 0}{\lim} \sin \theta =0[/latex]
Evaluating the Limit of Cosine as Theta Approaches Zero
To evaluate the limit of [latex]\cos(\theta)[/latex] as [latex]\theta[/latex] approaches zero, we rely on the fundamental Pythagorean identity which states that for any angle [latex]\theta[/latex], the square of the cosine of [latex]\theta[/latex] plus the square of the sine of [latex]\theta[/latex] equals one:
[latex]\cos^2(\theta)+\sin^2(\theta)=1[/latex]
Rearranging this identity, we can isolate [latex]\cos(\theta)[/latex]:
[latex]\cos(\theta)=\sqrt{1−\sin^2(\theta)}[/latex]
Since the sine function is bounded between [latex]-1[/latex] and [latex]1[/latex] for all [latex]\theta[/latex], and as [latex]\theta[/latex] approaches zero, [latex]\sin(\theta)[/latex] also approaches zero, we can substitute this limit into our identity:
[latex]\underset{\theta \to 0}{\lim} \cos \theta=\underset{\theta \to 0}{\lim} \sqrt{1−\sin^2(\theta)}[/latex]
Given that [latex]\underset{\theta \to 0}{\lim} \sin \theta =0[/latex], we then have:
[latex]\underset{\theta \to 0}{\lim} \sqrt{1−\sin^2(\theta)} =\sqrt{1-0^2}=1[/latex]
Thus, we confirm that the limit of [latex]\cos(\theta)[/latex] as [latex]\theta[/latex] approaches zero is [latex]1[/latex].
the limit of [latex]\cos(\theta)[/latex]
[latex]\underset{\theta \to 0}{\lim} \cos \theta =1[/latex]
Exploring the Limit of Sine Theta Over Theta
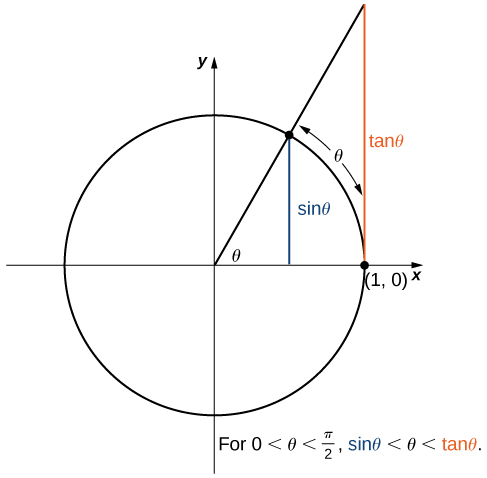
Analyze the behavior of [latex]\sin(\theta)[/latex] and [latex]\tan(\theta)[/latex] within the first quadrant of the unit circle, specifically for angles [latex]\theta[/latex] where [latex]0 < \theta < \frac{\pi}{2}[/latex].
In this range, it’s clear from the geometric representation that [latex]\sin(\theta)[/latex] is always less than the length of the tangent line segment from the point on the circle to the [latex]x[/latex]-axis, which is [latex]\tan(\theta)[/latex]. Consequently, we have the inequality:
By dividing each term in the inequality by [latex]\sin \theta[/latex] , we are led to:
With the reciprocal, this inequality can be restated as:
As [latex]\theta[/latex] approaches zero, [latex]\cos(\theta)[/latex] approaches [latex]1[/latex]. Therefore, [latex]\sin(\theta)[/latex] is squeezed between [latex]\cos(\theta)[/latex] and [latex]1[/latex].
Since [latex]\cos(\theta)[/latex] also approaches [latex]1[/latex] as [latex]\theta[/latex] approaches zero, the Squeeze Theorem can be applied to conclude that:
the limit of [latex]\dfrac{\sin \theta}{\theta}[/latex]
[latex]\underset{\theta \to 0}{\lim}\dfrac{\sin \theta}{\theta}=1[/latex]
Evaluating the Limit of [latex]\dfrac{1- \cos \theta}{\theta}[/latex]
As we build upon the understanding of limits involving trigonometric functions, the next step is to apply the Squeeze Theorem to evaluate limits that are not immediately obvious.
In the example below, we use the limit of [latex]\frac{\sin {\theta}}{\theta}[/latex] to establish [latex]\underset{\theta \to 0}{\lim}\frac{1- \cos \theta}{\theta}=0[/latex]. This limit also proves useful in later modules.
Evaluate [latex]\underset{\theta \to 0}{\lim}\dfrac{1- \cos \theta}{\theta}[/latex]
the limit of [latex]\dfrac{1- \cos \theta}{\theta}[/latex]
[latex]\underset{\theta \to 0}{\lim}\dfrac{1- \cos \theta}{\theta}=0[/latex]